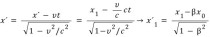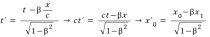시공간

시공간(space time, 時空間) 혹은 시공(時空)은 시간과 공간을 합친 것이다. 특히 상대성이론에서는 시간과 공간이 독립적이지 않고 서로 섞일 수 있음으로 시공간이라는 용어를 대체로 사용한다. 우리 세상은 3차원의 공간과 1차원의 시간을 합쳐 4차원의 시공간을 이룬다. 때로는 공간의 차원과 시간의 차원을 구분하여 (3+1)차원 시공간이라고 부르기도 한다.

개요

일반적인 3차원 공간과 1차원의 시간이 서로 조합되어 시공간의 4차원 다양체를 표현한다. 현대에 나온 초끈이론, 고리 양자 중력은 현재 표준적으로 고려되는 시공간 모델과 다른 모델을 제안했다. 예를 들어서 초끈이론에서는 우주의 시공간이 11차원이라고 주장한다. 고전 물리학에서는 뉴턴역학을 근거로 하며, 시간과 공간을 절대화하여 관측과는 독립하는 객관적으로 존재하는 범주로 보았다. 그러한 전제 아래 모든 물리현상을 거시적으로 다루었다. 그러나 관측자에 대한 시간과 공간의 상대화를 주장한 알베르트 아인슈타인(Albert Einstein)의 상대성이론이 나타나면서 그러한 전제가 무너졌다. 그러면서 양자역학에 의해 모든 물리 현상이 확률적, 통계적, 미시적으로 다뤄지면서 거시적 입장이 부정되었다.

상대성이론에 따라 모든 현상의 추이시간(推移時間)은 그 현상이 놓여 있는 공간의 상태(중력장의 영향)가 지배하에 있고 관측에 대한 상대운동에도 영향을 받는다. 이것은 여러 실험에서 확인이 되고 있다. 시간과 3차원 공간은 서로 독립적이 아니라 4차원 시공간으로 생각할 수 있으며, 4차원의 시공간의 회전을 로런츠변환이라 하는데, 이 변환에서는 시간 좌표와 공간 좌표가 대등한 변환을 받는다. 따라서 보편성, 균일성, 객관성을 갖춘 절대적 시간은 존재하지 않는다. 이때 4차원 시공간을 민코프스키 공간 혹은 민코프스키의 시공세계라고 하는데, 아인슈타인의 특수상대성이론의 기하학적 표현 수단이다.

민코프스키 공간

헤르만 민코프스키(Hermann Minkowski)

1907년 독일 수학자 헤르만 민코프스키(Hermann Minkowski) 최초로 사건들이 일어나는 장소와 시간을 따로 구분하지 않는 시공간으로 통합시키고 그에 걸맞은 기하학적 공간인 민코프스키 공간을 정의했다. 민코프스키는 1908년에 공간과 시간(Raum und Zeit)이라는 제목으로 연설하였는데, 이 연설은 지금도 유명하다.

Die Anschauungen über Raum und Zeit, die ich Ihnen entwickeln möchte, sind auf experimentell-physikalischem Boden erwachsen. Darin liegt ihre Stärke. Ihre Tendenz ist eine radikale. Von Stund’ an sollen Raum für sich und Zeit für sich völlig zu Schatten herabsinken und nur noch eine Art Union der beiden soll Selbständigkeit bewahren.

제가 여러분 앞에 제시하려는 공간과 시간에 대한 관점은 실험 물리학에서 유래합니다. 이 관점의 강점은 여기에 있습니다. 이 관점의 성격은 과격합니다. 앞으로 공간 자체 및 시간 자체는 마치 그림자처럼 사라질 것이고, 오직 그 둘의 합체만이 독립적인 실체로 남을 것입니다.

처음에는 전자기학의 맥스웰 방정식에 어울리는 배경을 만들고자 연구를 시작했지만, 특수 상대성 이론이 알려지면서 헤르만 민코프스키 자신의 연구 성과가 특수 상대성 이론을 가장 잘 형식화 한다는 것을 알았다. 이것은 우연의 일치는 아니다. 왜냐하면 특수 상대성 이론 자체가 맥스웰 방정식과 갈릴레이 변환의 불협화음을 해소하고자 하는 바람에서 연구가 진행되었으며, 결정적 단서들을 제공했기 때문이다. 민코프스키는 시간과 공간(장소)을 따로 보는 관념은 그림자처럼 사라지고 시공간 통일체만이 독립적 실체로 남을 것이라고 하였다. 시간과 장소를 기하학적으로 밀접하게 통합한 최초의 사례이자 시공간의 비 유클리드 기하학이라는 화두를 던짐으로써 물리학적 패러다임 전환을 이뤄냈으며 인류가 시공간에 대한 더 깊은 이해를 하도록 선도했다. 수학자들이 비 유클리드 기하학을 만든 지 약 100년 동안 수학밖에는 아무런 연관이 없었는데, 민코프스키 공간은 비 유클리드 기하학이 최초로 수학이 아닌 것과 깊은 연관성을 보여줬다. 민코프스키의 업적이 알려지면서, 알베르트 아인슈타인은 논문을 통해 민코프스키 공간을 물리학에 도입하는 것에 대해 공식적으로 회의적 시각을 드러냈고, 불필요한 박식함이라고 무시하기도 했다. 그러나 일반 상대성 이론을 연구하면서 민코프스키의 기하학적 접근이 필수라는 것을 깨달았다. 현대에는 시공간을 기술할 때 민코프스키 공간이 필수다. 일반적으로 시공간은 준 리만 다양체 기술되며, 이는 평평한 상황에 해당하는 민코프스키 공간을 휘어진 경우까지 일반화한 것이다

수학에서 민코프스키 공간(Minkowski space)은 선형공간 $\mathbb {R} ^{4}$에 특정한 쌍선형 형식
$\eta ={\begin{pmatrix}-1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{pmatrix}}$ 가 주어진 수학적 구조 $(\mathbb {R} ^{4},\eta )$이다. 간단한 준 리만 다양체의 예시라고도 본다.

공간의 3차원 벡터 ${\vec {x}}=(x,y,z)$ 를 확장하여 4차원 벡터 $x=(ct,x,y,z)$로 표현할 수 있다. 여기서 c는 빛의 속도이고 따라서 ct의 단위는 거리의 단위가 된다. t 대신 ct를 사용하는 이유는 x, y, z는 공간을 나타내므로 단위를 맞추려면 t 대신 ct를 사용한다. 치수가 다른 벡터의 구성 요소를 갖는 것은 의미가 없다. 어떤 물체가 시간 축(ct)을 따라서 움직인다면, 이것은 공간에서의 움직임이 아닌 시간을 통해 빛의 속도로 움직이고 있음을 의미한다. 아인슈타인에 의하면, 모든 관찰자는 그들은 정지해있지만 주위의 모든 것들이 움직이고 있다고 믿는다. 예를 들어 등속으로 달리는 기차 안에 있는 관찰자는 주위의 것들이 뒤로 밀려나는 것처럼 보이지만, 기차 밖에 서 있는 관찰자는 기차가 움직이는 것으로 보인다. 이것은 어떤 관찰자가 공간과 시간을 통해 여행할 때, 그들은 시공간에서 시간을 따라 움직이고 있다고 생각하는 것을 의미한다.

물리학에서의 시공간

뉴턴역학의 시공간

일상의 경험 및 그에 바탕을 둔 뉴턴역학에서는 시간과 공간은 아무 관계가 없고 누구나 하나의 시간을 공유한다. 우주 전체에 공통으로 하나의 절대시간이 흐른다고 생각하여 어떤 좌표계에서도 시간과 공간은 섞이지 않는 것이다. 예를 들어 어떤 관성계 $S$에 대해 다른 관성계 $S'$이 $x$방향으로 상대속도 $v$로 운동하면, 두 좌표계 사이에는 다음과 같은 갈릴레이변환 관계가 성립한다.

$t'=t,$     $x'=x-vt,$     $y'=y,$     $z'=z.$

즉, 두 좌표계의 시간은 $t'=t$로 변하지 않는다.

특수상대성이론의 시공간

그림 1. 특수상대성이론의 시공간 그림과 빛원뿔

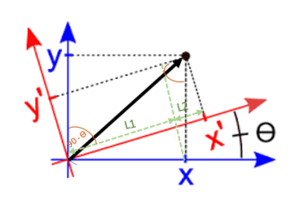
특수상대성이론의 기본 가정인 상대성원리와 광속 불변의 원리를 받아들이면 두 관성계는 다음과 같은 로런츠 변환 식을 만족시킨다.

$t'=\gamma (t-{v \over c^{2}}x),$     $x'=\gamma (x-vt),$     $y'=y,$     $z'=z.$

여기에서 $\gamma ={1 \over {\sqrt {1-v^{2}/c^{2}}}}$ 로서 로런츠 인자라고 한다. 이 변환 식을 보면 좌표계 $S$의 어떤 시간 $t$에 대해 공간좌표 $x$가 달라지면, 좌표계 $S'$에서는 시간 $t'$이 달라진다. 즉, 한 좌표계에서 위치의 차이가 다른 좌표계에서는 시간의 차이로 나타난다. 이처럼 시간과 공간이 서로 완전히 독립적이지 않고 섞이기 때문에 상대성이론에서는 시간과 공간을 분리하지 않고 시공간이라는 하나의 용어로 기술하는 것이 자연스럽다. 4차원 시공간에서의 한 점은 사건(event)이라 부르는 데 시간과 공간좌표를 모두 모은 $(t,x,t,z)$으로 나타낼 수 있다.
상대성 이론에서 시간과 공간이 섞이기는 하지만 성격을 완전히 바꿀 수는 없다. 관성계 $S$에서 원점 $(0,0,0,0)$과 어떤 사이의 간격(interval) $s^{2}$을 다음과 같이 정의해보자.

$s^{2}=-c^{2}t^{2}+x^{2}+y^{2}+z^{2}.$

위의 로런츠 변환에 의해 관성계 $S'$에서 간격 $s^{2}$을 계산해보면 변하지 않는 것을 알 수 있다. 즉,

$s'^{2}=-c^{2}t^{2}+x^{2}+y^{2}+z^{2}=-c^{2}t^{2}+x^{2}+y^{2}+z^{2}=s^{2}$

이다. 수학 용어로는 이런 시공간을 민코프스키 시공간이라 부른다. 예를 들어, 관성계 $S$에서 시간 $t$에 원점에서 발생한 어떤 사건의 간격은 $s^{2}=-c^{2}t^{2}<0$이다. 그러면 로런츠 변환에 의해 관성계 $S'$에서는 이 사건이

$t'=\gamma t,$     $x'=-\gamma vt,$     $y'=y,$     $z'=z$

에서 일어나게 되어 시간과 공간이 섞였지만, 간격은

$s'^{2}=-c^{2}\gamma ^{2}t^{2}+(-\gamma vt)^{2}=-c^{2}t^{2}=s^{2}$

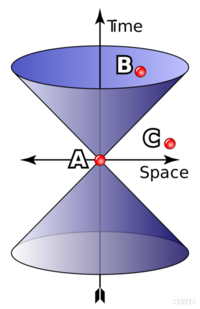
으로 변하지 않는다. 특히 간격의 부호가 여전히 음수다. 이처럼 어떤 사건 $(t,x,y,z)$는 간격 $s^{2}$이 양수인지, 음수인지, 혹은 0이냐에 따라 세 종류로 구분할 수 있고 이 구분은 로런츠 변환 때문에 시간과 공간이 섞여도 변하지 않는다. $s^{2}<0$인 경우를 시간꼴(timelike)이라 하고 $s^{2}>0$을 공간꼴(spacelike), $s^{2}=0$을 빛꼴(lightlike) 혹은 그냥 영(null)이라 한다. $s^{2}=0$인 빛꼴 사건들을 모두 모은 것을 빛원뿔(light cone)이라 한다. 편의상 방향을 생략하고 2차원 공간과 시간만을 고려했을 때 빛꼴 사건들이 그림 1처럼 원뿔을 이룬다. 그림 1은 시공간 그림(spacetime diagram)이라고 부르는데 수직축은 시간을 나타내고 아래쪽이 과거, 위쪽이 미래다. 수평면은 $xy$ 공간을 나타낸다. 원뿔의 꼭짓점을 원점 A로 잡았을 때 원뿔의 내부인 점 B는 시간꼴이고 외부인 점 C는 공간꼴이다. 질량이 있는 물체는 빛보다 빠르게 운동할 수 없음으로, A에 있는 물체는 원뿔 내부로만 움직일 수 있다. A에서 C로 이동하거나 영향을 주는 것은 불가능하다. 빛은 항상 빛의 속도로 움직이므로 A에서 출발한 빛은 빛원뿔 위의 한 직선을 따라 움직인다.

광속 중심의 관점

광속은 빛의 속도로, 대략 말하자면 빛이 이동한 거리를 그동안 걸린 시간으로 나누면 구할 수 있다. 광속이라는 개념에는 시간과 공간이 함께 들어가 있다. 이는 광속이라는 우주의 언어를 시간과 공간이라는 인간의 언어로 번역 혹은 해석한 결과라고 볼 수 있다. 갈릴레오와 뉴턴 이래 고전물리학이 한 일은 인간의 언어로 번역하는 방식이었다. 아인슈타인은 이것을 뒤집었다. 우주를 정확하게 기술하려면 우주 본연의 언어를 이용해야 한다. 시간과 공간이 아니라 광속을 중심에 놓고 자연을 기술해야 한다. 따라서 시간과 공간으로 광속을 이해할 것이 아니라, 광속을 중심으로 시간과 공간을 번역하고 해석해야 한다. 광속불변이라는 특수상대성이론의 두 번째 가정의 진정한 의미는 바로 이것이다. 광속이라는 개념에는 시간과 공간이 함께 들어가 있다. 따라서 상대적인 운동이 어떠하든 광속이 불변이려면 상대적인 운동에 따라 시간과 공간이 분리되어 놀 수가 없고 모종의 방식으로 서로 얽혀들어야만 한다. 이는 고전역학에서는 있을 수 없는 일이다. 고전역학에서는 시간은 시간이고 공간은 공간일 뿐으로 각각은 서로 독립적이다. 그러나 상대성이론에서는 시간과 공간이 서로 독립적이지 않다. 이들은 하나의 시공간을 형성해 서로 유기적으로 관계를 맺어야만 한다. 그 결과 상대성이론에서는 1차원의 시간과 3차원의 공간이 따로 존재하지 않고 이들이 하나로 합쳐진 4차원 시공간을 형성한다. 그 결과 시간과 공간이 운동 상태에 따라 달라진다. 이는 상대적인 운동에 따라 물리법칙과 광속을 항상 똑같이 유지하기 위해 치러야 할 대가다. 고전역학에서는 눈에 보이는 현상과 절대적인 시간 및 공간을 유지하기 위해 상대적인 운동에 따라 물리법칙(방정식)과 광속이 변했다. 상대성이론에서는 그 반대이다. 결론만 말하자면 움직이는 좌표계의 시간이 늦게 가고 진행 방향의 길이가 짧아진다. 고전역학에서는 상상도 못 할 일이다. 시간이 느려진다는 것은 정확히 말해 1초의 간격이 길어진다는 뜻이다. 이를 시간 팽창이라 부른다. 정지한 사람이 봤을 때 움직이는 좌표계 속에서의 모든 것이 슬로우 모션으로 움직인다. 시간이 팽창하는 정도는 속도의 함수로 주어지는데 광속에 가까울수록 그 효과가 아주 커진다. 반면 우리가 일상에서 접하는 느린 속도(광속보다)에서는 시간 팽창 효과가 미미하다.

시간이 팽창하는 딱 그만큼 진행하는 방향의 길이도 짧아진다. 황당한 사이언스 픽션(SF) 소설 같은 얘기로 들리겠지만, 모두 사실이다. 지난 100여 년 동안 엄격한 실험과 검증도 모두 통과했다. 예컨대, 소립자 중에 뮤온이라는 입자가 있다. 전자와 모든 물리적 성질이 비슷하지만, 질량만 전자보다 200배 남짓 더 무겁다. 뮤온의 수명은 약 백만 분의 2초이다. 뮤온은 우주에서 날아온 입자들에 의해 지구 대기의 상층에서 만들어진다. 고전역학의 관점에서 보자면 뮤온이 광속(초속 약 3억 미터)으로 날아간다고 하더라도 수명이 백만 분의 2초니까 비행거리가 겨우 600m에 불과하다. 많은 수의 뮤온이 대기 상층에서 만들어지더라도 대부분은 금세 다른 입자들로 붕괴해 버리기 때문에 지표면까지 도달하는 뮤온의 개수는 극히 적다. 실제 실험에서는 예상보다 훨씬 많은 수의 뮤온이 지표 근처에서 검출된다. 그 이유는 광속에 가까운 속도로 비행하는 뮤온의 시간이 늦게 가기 때문이다. 즉, 지표면에 가만히 있는 우리에게는 이미 백만 분의 2초가 지났더라도 비행 중인 뮤온의 시계는 천만 분의 2초가 지났을 수도 있다. 그 결과 실제 뮤온은 고전역학에서 예상하는 것보다 훨씬 먼 거리를 날아갈 수 있다. 뮤온의 관점에서 바라보면, 뮤온과 함께 움직이는 좌표계에서는 뮤온은 정지해 있고 지면이 뮤온에게 빠른 속력으로 다가오고 있다. 이 좌표계에서는 뮤온의 시간이 팽창되지 않는다. 뮤온은 100만분의 2초의 수명을 살 뿐이다. 다만 뮤온과 지면 사이의 길이가 수축한다. 그 결과 뮤온은 짧은 생을 살면서도 지면 가까이에 도달할 수 있다. 지구 대기의 상층에서 만들어진 뮤온이 지표면 가까이 도달할 수 있다는 결과는 똑같지만, 그 과정은 지구 표면에 정지한 좌표계와 뮤온과 함께 움직이는 좌표계에서 전혀 다르다. 이처럼 상대성이론에서는 눈에 보이는 현상이 좌표계에 따라 얼마든지 다를 수 있다. 이는 물리법칙과 광속이 어느 관성좌표계에서나 똑같아야만 한다는 조건을 만족하기 위한 대가이다.

일반상대성이론의 시공간

특수상대성이론의 시공간은 시간과 공간이 섞이긴 하지만 여전히 평평하다. 그러나 일반상대성이론에서는 시공간이 휘어질 수 있다. 일반상대성이론은 물리법칙이 로런츠변환뿐 아니라 일반적인 좌표변환(general coordinate transformation)에 대해서도 그대로 성립해야 한다는 기본 원리를 바탕으로 만들어졌다. 이로부터 아인슈타인 방정식이 유도된다. 이에 따르면, 시공간의 에너지 분포가 시공간을 휘게 만들고 그 휘어진 정도가 중력으로 나타난다. 블랙홀은 시공간이 극단적으로 휜 경우인데 중력이 너무 강하여 빛조차도 블랙홀을 빠져나오지 못한다. 시공간은 에너지 분포에 따라 휘어질 뿐 아니라 그 자체가 출렁이면서 시간에 따라서 역동적으로 변화하여 파동을 만들어낼 수 있다. 이것을 중력파라 한다. 아인슈타인은 1916년에 처음으로 중력파의 존재를 예언했는데 그로부터 100년이 지난 2016년에 처음으로 중력파가 실제로 발견되었다.

시공간은 휘어져 있는가?

아인슈타인 제안한 일반상대성이론에 의하면 질량 주위의 시공간은 질량의 영향으로 휘어져 있다. 중력은 뉴턴이 주장했건 것처럼 두 물체 사이의 원격 작용에 의해 작용하는 힘이 아니라, 휘어진 시공간 곡률 때문에 작용한다는 것이 일반상대성이론의 설명이다. 미국의 물리학자 존 휠러(John Archibald Wheeler)는 이것을 '물질은 공간의 곡률을 결정하고, 공간은 물질의 운동을 결정한다.'라고 말을 전했다.

• 공간이 휘어졌다는 것은 무엇을 의미하는가?

평면이 휘어졌다는 것은 쉽게 이해할 수 있다. 그것은 우리가 3차원 공간에 살고 있어서 평면을 3차원에서 바라볼 수 있기 때문이다. 2차원밖에 모르는 생명체가 존재한다면 그런 생명체도 자신이 살고 있는 평면이 휘어졌다는 것을 아는 방법이 있다. 만약 큰 삼각형을 그려서 내각의 합을 재보면 자신이 있는 평면이 평평한지 휘어져 있는지 알 수 있다. 휘어진 평면 위에 그린 삼각형의 내각의 합은 180도가 아니기 때문이다. 3차원 공간에 살고 있는 우리도 여러 가지 기하학적 측정을 통해 우리 공간이 휘어져 있다는 것을 알 수 있다. 공간이 휘어져 있다는 것은 우리가 사는 공간이 중고등학교에서 배운 기하학과 맞지 않는 공간이라는 것을 뜻한다. 우리가 어려움을 겪고 있는 것이 우주 공간이 간단한 측정으로는 그것을 알아챌 수 없을 정도로 조금 휘어져 있기 때문이다.

• 증거 1. 수성의 근일점 변화

수성의 근일점 변화

1915년 일반상대성이론이 제안된 이래 많은 과학자가 시공간이 휘어져 있다는 것을 확인하기 위해 수많은 실험을 했다. 태양 주위의 시공간이 휘어져 있다는 첫 번째 증거는 수성의 근일점 변화다. 수성의 근일점은 수성이 태양과 가장 가까운 점을 말한다. 프랑스의 천문학자 위르뱅 장 조제프 르베리에(Urbain Jean Joseph Le Verrier)가 수성의 근일점이 움직여 간다는 것을 발견한 시점으로, 이것은 태양계의 풀어야 할 숙제였다. 수성의 근일점은 100년마다 5,600초 움직여 가는데 이 중의 5,557초에 대해서는 뉴턴 역학으로도 설명할 수 있지만, 43초에 관해서는 설명할 수 없었다. 일반상대성이론은 휘어진 시공간을 이용해 이 43초를 설명하는 데 성공했다. 아인슈타인은 일반상대성이론으로 이것을 설명하고 난 후 친구에게 심장이 고동쳤고 흥분으로 여러 날 잠을 이루지 못했다는 편지를 보냈다. 오른쪽 사진을 참고하면, 수성의 궤도는 빨간 선과 같이 고정된 것이 아니라, 파란 선과 같이 계속 움직인다. 근일점도 따라서 매우 조금씩 변한다. 수성의 근일점 변화의 이해를 돕기 위한 그림이다.

• 증거 2. 태양을 지나는 빛의 휘어짐

은하단(Abell2218)

시공간이 휘어져 있다는 두 번째 증거는 태양과 같이 큰 질량 주위를 지나가는 빛이 휘어져 간다는 것이다. 1919년 영국의 아서 스탠리 에딩턴(Sir Arthur Stanley Eddington)이 이끄는 영국의 탐사팀은 일식 때 태양 옆을 지나온 별빛을 측정하여 별빛이 일반상대성이론에서 예측한 대로 태양 주위의 휘어진 시공간을 통과하면서 휘어진다는 것을 밝혀냈다. 그 이후 수많은 일식 관측을 통해 에딩턴의 결과가 증명되었다. 1960년대에는 여러 개의 전파 망원경(VLBI)을 사용하여 먼 별에서 오는 전파가 태양 부근을 지날 때 휘어지는 정도를 측정하여 에딩턴이 얻었던 결과보다 훨씬 정밀한 결과를 얻었다. 관측 기술의 발전에 따라 태양보다 질량이 훨씬 작은 목성에 의해 빛이 휘는 것도 50%의 오차 내에서 관측이 가능하게 되었다. 오른쪽 그림을 참고하면, 은하단(Abell2218) 주변에 길고 희미한 호가 보인다. 이 호는 사실 더 멀리 있는 은하다. 은하단 중력에 의해서 빛이 휘어 왜곡되어 보이는 것이다.

• 증거 3. 중력에 의한 적색편이

1960년대에는 지상에서 휘어진 시공간을 측정하려는 실험이 시도됐다. 시공간의 곡률이 다르면, 즉 중력장의 세기가 다르면 시간이 다르게 가기 때문에 같은 원자가 내는 전자기파의 진동수와 파장이 약간 달라진다. 이것을 중력에 의한 적색편이라 부른다. 하버드 대학 구내에는 높이가 22m인 제퍼슨 탑이 있다. 1960년 로버트 비비안 파운드(Robert Vivian Pound)와 글렌 레브카(Glen Anderson Rebka) 그리고 스니더(J. L. Snider)는 탑 위에 있는 원자가 내는 감마선을 탑 아래에 있는 원자가 흡수하도록 하는 실험을 통해 오차 한계 내에서 일반상대성이론의 예측치에 일치하는 결과를 도출했다. 이러한 실험은 인공위성을 이용하여 계속되었다. 지구상에 있는 원자시계와 토성 궤도를 지나고 있던 보이저 탐사선과 태양을 부근을 지나고 있던 갈릴레오 탐사선에 실려 있는 시계를 비교한 실험에서도 예상했던 것과 같은 정도의 중력에 의한 적색편이가 측정되었다. 가장 정확한 중력에 의한 적색편이 측정은 1976년에 로버트 베소(Robert Vessot)와 마틴 레빈(Martin Levine)이 행한 인공위성(Gravity Probe-A)을 이용한 실험이었다. 이 실험에서는 지상에 있는 수소 원자시계와 1만 km 상공에서 지구를 돌고 있던 인공위성에 실려 있는 같은 종류의 시계를 비교하여 이론적인 값과 0.02%의 오차 내에서 일치하는 결과를 도출했다. 재미있는 것은 전혀 의도하지 않았던 위치 추적 장치(GPS)가 중력에 의한 적색편이 현상을 증명하고 있다는 것이다. GPS가 15m의 오차 범위 내에서 위치를 결정하기 위해선 위성이 가지고 있는 시계의 오차는 50나노초 이내여야 한다. 이것은 GPS 위성의 고도인 20,000km 상공에서의 중력효과의 이론값인 40마이크로초보다 훨씬 작은 값이다. 따라서 상대성이론에 의한 효과를 고려하지 않으면 정확한 위치를 결정하는 것이 불가능하다. 우리가 매일 사용하고 있는 GPS는 일반상대성이론의 정당성을 증명해주고 있다.

• 증거 4. 태양 부근을 지나는 전자기파의 느려짐

1964년 미국의 천문학자 어윈 아이라 샤피로(Irwin Ira Shapiro)는 만약 일반상대성이론이 옳다면, 태양 부근을 지나는 행성이나 인공위성의 전자기파는 휘어진 시공간의 영향으로 느려져야 한다고 지적하였으며, 다른 행성과 인공위성을 이용하여 이런 효과를 측정할 것을 제안했다. 그의 제안에 따라 수성과 화성을 지구에서 보았을 때, 태양 반대편에 위치할 경우 전자기파를 보낸 뒤 반사되어 온 전자기파를 측정하는 실험을 했다. 수성과 화성에 의해 반사된 빛은 5%의 오차범위 내에서 일반상대성이론의 예측과 일치했다. 1976년에 행한 화성에 착륙한 바이킹 탐사선이 반사한 신호를 이용한 실험에서는 오차가 0.1% 이내로 줄었다. 마리너 6호와 7호, 그리고 보이저 2호와 같은 우주 탐사선을 이용해서도 같은 실험을 진행했다. 2003년에는 토성으로 향하는 카시니 탐사선을 이용하여 정밀한 샤피로 시간 지연 실험이 진행되었다. 실험 결과는 오차 범위 0.002% 내에서 일반상대성이론과 일치했다.

• 증거 5. 중력 측정 위성-B(Gravity Probe B, GP-B) 이용한 중력 측정

중력측정위성-B의 부품, 자이로스코프의 회전자와 케이스

2004년에는 지구 질량에 의해 휘어져 있는 시공간을 직접 측정하려는 연구를 위해 중력 측정 위성-B(Gravity Probe B, GP-B)가 지구 궤도에 올려졌다. 스탠퍼드 대학 연구팀이 주관하는 이 프로젝트는 1959년에 처음 제안되었으며, 1964년부터 미항공우주국(NASA)에서 연구비를 제공해온 프로젝트로 NASA에서 추진하고 있는 물리학 연구 프로젝트 중에서 가장 오래 지속되고 있는 프로젝트였다. 중력 측정 위성-B가 측정하려는 것은 두 가지였다. 첫 번째는 지구의 질량에 의해 휘어진 시공간을 측정하는 것이고 두 번째는 지구가 태양 주위를 공전하면서, 이 휘어진 시공간을 끌고 가는 효과를 측정하려는 것이다. 이 인공위성에는 네 개의 정교한 자이로스코프가 실려 있다. 자이로스코프는 회전 관성에 의해 항상 같은 방향을 유지하도록 고안한 장치로 비행기가 비행할 때 방향을 정하기 위해 사용된다. 중력 측정 위성-B에 실려 있는 자이로스코프는 페가수스자리의 IM 별(IM Pegasi)을 향해 고정되었다. 만약 지구 주위의 공간이 휘어져 있지 않다면, 중력 측정 위성-B가 지구를 공전하는 동안, 이 자이로스코프들은 항상 이 별을 향하고 있어야 한다. 그러나 지구 주위의 시공간이 휘어져 있다면, 위성이 지구의 반대편에 왔을 때는 자이로스코프의 방향이 달라져 있을 것이다. 중력 측정 위성-B의 측정 결과에 의하면, 페가수스자리의 IM 별에 정확하게 정렬 시켜 놓았던 중력 측정 위성-B의 자이로스코프는 1년 동안에 6.606초(0.0018도) 정도 방향을 바꾸는 것으로 판명되었다. 이 결과는 1%의 오차 범위 내에서 일반상대성이론의 예상과 일치했다. 중력 측정 위성-B 프로젝트의 책임자인 스탠퍼드 대학의 프랜시스 에버리(Francis Everitt)는 '자이코스코프를 이용해 지구 주변에 휘어진 공간을 직접 측정할 수 있는 것은 놀라운 일이다.'라고 말했다. 그러나 지구의 공전에 의해 휘어진 공간을 끌고 가는 효과는 아직 측정 중이다. 이론에 의하면 이 효과에 의해 자이로스코프의 지전축이 0.039초(0.000011도) 정도 달라져야 한다. 이것은 휘어진 시공간 효과의 170분의 1이다. 스탠퍼드 연구팀은 관측 자료에서 이 값을 찾아내기 위해 노력하고 있다.

• 증거 6. 중력파

중력파 관측은 이론적으로 예견만 되었던 중력파를 실측하게 된 것을 의미한다. 2016년 2월 11일, 레이저 간섭계 중력파 관측소(LIGO) 및 버고 합동연구진은 중력파를 최초로 관측하는 데 성공했음을 발표했다. 독일 하노버 알베르트 아인슈타인 연구소의 물리학자 마르코 드라고(Marco Drago)가 2015년 9월 14일에 검출한 파형은 나선을 그리며 떨어지는 한 쌍의 블랙홀의 병합과 그 결과로 형성된 단일 블랙홀의 신호(ringdown) 대한 일반상대론의 예측과 일치하였다. 이 신호에는 GW150914라는 명칭이 붙여졌다. 이는 블랙홀 쌍성의 병합에 관한 첫 관측으로, 항성 질량 블랙홀 쌍성계의 존재와 그들의 병합이 최근의 우주에도 발생하고 있음을 보여준다.

시공간 간격

시공간 간격(spacetime interval)은 시간을 포함하는 두 사건 사이의 공간을 말한다. 시공간 간격은 변하지 않는 양이므로 매우 중요하다.
$x'=x\cos \theta -y\sin \theta$, $y'=-x\sin \theta +y\cos \theta$ 두 식은 고전 역학과 다르게, 로런츠 변환이 선형 변환이라 서로 다른 기준계인 상대성 이론에서는 맞지 않는다.

$x^{2}+y^{2}=x'^{2}+y'^{2}$ 기준계가 달라도 시공간 간격은 항상 일정하다.

$t^{2}+x^{2}$이 성립되지 않는 이유는 우선 시간은 기준계에 따라 다르고 시간 t와 장소 x의 단위가 다르기 때문이다. 좌표에서 $X=(X_{0},X_{1})=(ct,x)$를 의미하고 $X=(X_{0},X_{1},X_{2},X_{3})=(ct,X_{1},X_{2},X_{3})=...$ 이다.

로런츠 변환에서 t → ct로 수정하면,

$B=v/c$, $x_{2}=x'_{2}$, $x_{3}=x'_{3}$

로런츠 변환에서 시간과 장소가 공존했지만, 상대성 이론에서는 간단하게 서로 대칭이된다.
$x0^{2}+x_{1}^{2}\neq x\prime 0^{2}+x\prime _{1}^{2}$
$x\prime 0^{2}-x\prime _{1}^{2}=x0^{2}+\beta x_{1}^{2}-2\beta x0x_{1}-x_{1}^{2}-\beta ^{2}x0^{2}+2\beta x_{1}x0=x0^{2}-x_{1}^{2}$
$S^{2}=S'^{2}$이므로 시공간 간격은 항상 일정하다.
$S^{2}=(c\Delta t)^{2}-(\Delta x_{1})^{2}-(\Delta x_{2})^{2}-(\Delta x_{3})^{2}$

$S^{2}>0$ 시간과 같은 간격으로 두 사건은 인과관계로 연결되어 있다. $S^{2}<0$ 공간과 같은 간격으로 두 사건은 인과관계로 연결되어 있지 않다. 현재에서 과거로 가려면 빛보다 빨리 가야 하는데 빛은 우주 속도의 한계이므로 과거로 가기에는 시간이 모자라다. $S^{2}=0$은 빛과 같은 간격으로 두 사건은 오직 광속으로만 움직인다.

시공간은 로런츠 공변성이 있고 이것이 시공간의 대칭성을 극명하게 보여준다. 등방(isotropic)한 공간은 회전에 대한 대칭성이 있으며, 벡터의 길이 ${\vec {x}}\cdot {\vec {x}}$를 일정하게 보존한다. 로런츠 공변성은 시공간 벡터의 길이 $x\cdot x=(ct)^{2}-{\vec {x}}\cdot {\vec {x}}$를 일정하게 보존한다. 공간은 데카르트의 직교 좌표계로 잘 표현되듯이 시공간은 헤르만 민코프스키의 민코프스키 좌표계로 표현할 수 있다.

시공간을 초월하는 메타버스

메타버스(metaverse)는 가상·초월(meta)과 우주(universe)의 합성어로 3차원 가상세계를 의미한다. 구체적으로는 정치와 경제, 사회 그리고 문화의 전반적 측면에서 현실과 비현실 모두 공존할 수 있는 생활형, 게임형 가상세계라는 넓은 의미로 사용된다.

참고자료

• 〈시공간〉, 《네이버 지식백과(물리학백과)》
• 〈시공간〉, 《네이버 지식백과(두산백과)》
• 〈시공간〉, 《위키백과》
• 〈민코프스키 공간〉, 《위키백과》
• 이종필 건국대 상허교양대 교수, 〈(사이언스N사피엔스)시간과 공간이 아닌 시공간〉, 《동아사이언스》, 2021-04-01
• 〈시공간은 휘어져있나?〉, 《네이버 지식백과(네이버캐스트)》
• 〈중력파 관측〉, 《위키백과》
• Soo, 〈특수 상대성 이론 - 민코프스키 시공간과 시공간 간격〉, 《네이버 블로그》, 2019-03-02
• 〈메타버스〉, 《위키백과》
• 장서연 기자, 〈‘시공간 초월 메타버스’…시니어 치매 예방에 효과?〉, 《더데일리포스트》, 2021-06-27
• 박민주 기자, 〈의료 현장에도 '메타버스' 시대 도래 ... 시공간 초월 의료 교육 현실화〉, 《헬스코리아뉴스》, 2021-05-31

같이 보기

• 시간
• 공간
• 1차원
• 2차원
• 3차원
• 4차원
• 상대성이론

이 시공간 문서는 메타버스에 관한 글로서 검토가 필요합니다. 위키 문서는 누구든지 자유롭게 편집할 수 있습니다. [편집]을 눌러 문서 내용을 검토·수정해 주세요.

개발 : 프로그래밍, 소프트웨어, 데이터, 솔루션, 보안, 하드웨어, 컴퓨터, 사무자동화, 인터넷, 모바일, 사물인터넷, 게임, 메타버스 □■⊕, 디자인 메타버스 개념 MZ세대 • 거울세계 • 다중우주(멀티버스) • 디지털 교육 • 디지털 기술 • 디지털 트윈 • 디지털 휴먼 • 라이프로깅 • 라이프로깅 메타버스 • 마이크로버스 • 메타버스 • 메타버스 교육 • 메타버스 기술 • 메타버스 기업 • 메타버스 복권 • 메타버스 사무실 • 메타버스 서비스 • 메타버스 솔루션 • 메타버스 쇼핑 • 메타버스 쇼핑몰 • 메타버스 시대 • 메타버스 시장 • 메타버스 아트 • 메타버스 정부 • 메타버스 콘서트 • 메타버스 콘텐츠 • 메타버스 테마파크 • 메타버스 프로젝트 • 메타버스 플랫폼 • 배틀로얄 • 스마트러닝 • 엔터테인먼트 • 제트세대 • 파티로얄 가상현실 0차원 • 1차원 • 2D(2차원) • 3D(3차원) • 3D 영화 • 3D 영화관 • 4D(4차원) • 4D 영화 • 4D 영화관 • 5차원 • 11차원 • 가로 • 가상 • 가상경제 • 가상공간 • 가상부동산 • 가상사무실 • 가상세계 • 가상재화 • 가상캐릭터 • 가상현실 • 가상현실 다큐멘터리 • 가상화폐 • 개더타운 • 거리 • 곡선 • 공간 • 과거 • 구 • 길이 • 너비 • 높이 • 도형 • 디지털 지구 • 면 • 면적 • 물리공간 • 미래 • 방향 • 비현실 • 선 • 세계 • 세로 • 세상 • 시간 • 시공간 • 아날로그 지구 • 엔터테인먼트 메타버스 • 우주 • 원 • 이동 • 입체 • 점 • 증강현실 • 지구 • 직선 • 차원 • 팬덤 • 평면 • 평행우주 • 현실 • 현실세계 • 현재 • 혼합현실 • 확장현실 메타버스 기술 3D 아바타 • 3D 모델링 • 3D 스캐너 • 3D 스캐닝 • 3D 안경 • 3D 프린터 • 3D 프린팅 • 3D 협업 솔루션 • 4D 프레임 • 4D 프린팅 • AR글래스 • IVAS • VIT 솔루션 • 게임엔진 • 구글 어스 • 그리드 컴퓨팅 • 딥 인터랙티브 • 렌더링 • 립모션 • 마커 • 마커리스 • 마커리스 캡처 • 메타버스 공간 관리자 • 메타버스 크리에이터 • 모델링 • 모션캡처 • 배틀 • 버추얼 유튜버 • 본캐 • 부캐 • 분산컴퓨팅 • 수중모션캡처 • 스캔 • 스테레오스코프 • 슬램 • 아바타 • 아바타 신분증 • 아이템 • 언리얼 엔진 • 에이알코어 • 에이알키트 • 영상지도 • 위성사진 • 유니티 • 인터랙티브 • 인터랙티브 콘텐츠 • 캐릭터 • 캐릭터 스캔 • 캡처 • 퀘스트 • 크리에이터 • 특수효과 • 특징점 • 페이셜 캡처 • 페이스북 스페이스 • 프린팅 • 핸드트래킹 • 핸드캡처 • 홀로그램 • 홀로렌즈 메타버스 서비스 가상화폐 • 구글 어스 • 동물의숲 • 디센트럴랜드 • 레디 플레이어 원 • 로블록스 • 도토리 • 디센트럴랜드재단 • 린든달러 • 마나 • 마이스페이스 • 마미손 • 마인크래프트 • 매트릭스 (영화) • 메타렉스 • 메타폴리스 • 미네르바 스쿨 • 배달의 민족 • 버추얼어스 • 사이버머니 • 사이펄리 • 세컨드라이프 • 스노우 • 스노우 크래시 • 시라 • 아바타 (영화) • 아이러브스쿨 • 암호화폐 • 어메이저 • 어스2 • 업랜드 • 에어비앤비 • 엑스알스쿨 • 엑스알스포츠 • 엑스알판도라 • 옴니버스 • 웨이브 • 위즈랩 • 유니버스 • 유알비타 • 이프랜드 • 인게이지 • 인피니트 오피스 • 제페토 • 젬 • 클래스브이 • 트윈월드 • 포트나이트 • 포트나이트 콘서트 • 호라이즌 메타버스 기업 ㈜갤럭시코퍼레이션 • 네이버랩스 • 네이버제트㈜ • 더디머티리얼라이즈드 • ㈜더블미 • 린든랩 • 드레스엑스 • ㈜맥스트 • 메타버스 얼라이언스 • ㈜모인 • ㈜비브스튜디오스 • ㈜비전브이알 • ㈜빌드잇 • ㈜싸이월드 • 쓰리아이 • ㈜아이스크림미디어 • ㈜아이스크림에듀 • 아티팩트스튜디오 • ㈜알체라 • ㈜어메이저 • ㈜에이트원 • 에픽게임즈 • 오큘러스 • 와이에이치데이타베이스(YHDATABASE) • ㈜위즈스쿨 • 유니티코리아 • 유니티 테크놀로지스 • ㈜이브이알스튜디오 • 일드길드게임즈 SEA • ㈜페트라인텔리전스 • 퓨처VR랩 • ㈜프론티스 • 플러스에이㈜ • ㈜한컴인텔리전스 메타버스 인물 벤 넬슨 • 이반 서덜랜드 위키 : 자동차, 교통, 지역, 지도, 산업, 기업, 단체, 업무, 생활, 쇼핑, 블록체인, 암호화폐, 인공지능, 개발, 인물, 행사, 일반