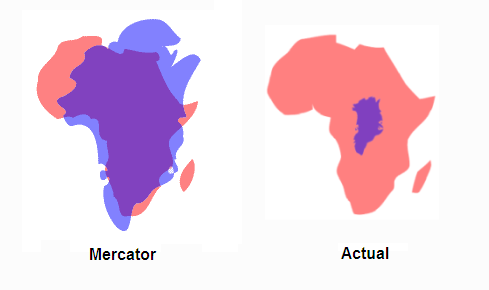
메르카토르 도법
메르카토르 도법(Mercator projection) 또는 점장도법(漸長圖法)은 네덜란드의 지도학자 헤르하르뒤스 메르카토르(H. Mercator)가 고안한 지도 투영법을 말한다. 메르카토르 도법으로 그려진 지도에서 두 점을 이은 선은 지구 경선에 대해 항상 같은 각도를 유지한다는 특징 때문에(특징 문단 참조), 등각 항로용 지도로서 항해에 널리 이용되었으며, 대항해시대 이후 전문가와 대중을 막론하고 가장 보편적인 지도 투영법으로 자리잡았다.
목차
개요
메르카토르 도법은 1569년 네덜란드의 게르하르두스 메르카토르가 발표한 지도 투영법으로서 벽지도에 많이 사용하는 대표적 도법이다. 원통중심도법과 원통정적도법을 절충한 이 도법은, 경선의 간격은 고정되어 있으나 위선의 간격을 조절하여 각도관계가 정확하도록(정각 도법) 되어 있다. 따라서 적도에서 멀어질수록 축척 및 면적이 크게 확대되기 때문에 위도 80' ~ 85' 이상의 지역에 대해선 사용하지 않는다. 이 도법의 가장 큰 특징은 지도 상 임의의 두 지점을 직선으로 연결하면 항정선과 같아진다는 것이다. 따라서 항해용 지도로 많이 사용해 왔다. 또 방향이나 각도 관계가 정확하므로 해류나 풍향 등을 나타내는 지도에도 많이 사용한다.
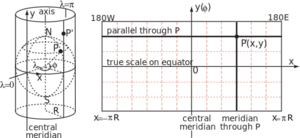
투영원리
지구를 표면이 유리인 구슬이라고 가정하자. 직사각형의 커다란 종이로 지구를 적도를 따라 감싼 다음에 중심에서 전구를 켜면, 지구 표면의 그림자가 종이에 비치게(투영되게) 된다. 이 그림자를 그대로 따라 그린 다음에 말았던 종이를 펴면 원통중심 도법 지도가 만들어진다. 이 방법은 이해하기는 가장 쉬우나 극 방향으로 갈수록 지도가 대책없이 커진다는 문제가 있어서 실질적으로는 양 극지방의 끝을 생략해서 지도를 그린다.
이거보다 조금 더 나은 방법으로 스테레오 투영법이 있는데, 위에서 쓴 구슬의 남극이나 북극을 종이에 대 놓고 전구는 반대쪽 극에서 켜는 것으로, 지구 표면의 그림자는 전구와 지구 표면을 잇는 직선 상에 투영된다. 이 도법은 지구상의 각을 그대로 보존한다. 메르카토르 도법은 수학적으로 스테레오 투영법으로 그린 지도를 복소평면으로 취급하고 그 지도를 로그함수에 입력한 출력값과 동일하며, 복소함수론에 따르면 로그함수는 등각사상, 즉 평면상의 각을 그대로 보존해서 다른 평면을 만드는 함수이므로, 메르카토르 도법 역시 지구상의 각을 그대로 보존한다.
특징
지도를 보는 사람이 지도를 보며 알기를 원하는 것은 두 지점 사이의 방향, 두 지점 간 거리, 경선과 위선 사이 각도, 지구 위 특정한 영역의 면적 등 4가지를 들 수 있다. 그런데 이 중 하나를 정확하게 나타내려면 나머지 셋을 포기해야 한다. 방향을 정확하게 나타내면 방위 도법, 거리를 정확하게 나타내면 정거 도법, 각도를 정확하게 나타내면 정각 도법[2], 면적을 정확하게 나타내면 정적 도법, 그리고 방향, 거리, 각도, 면적 중 어느 하나도 정확하진 않으나 모두 적당히 만족할 경우에는 절충 도법이라고 한다. 메르카토르 도법은 정각 도법의 일종이다.
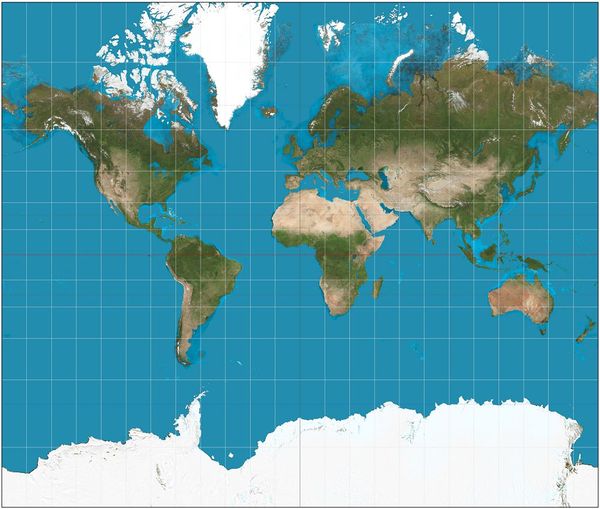
우리가 가장 흔히 볼 수 있는 세계지도는 수많은 투영법 중의 하나인 메르카토르 투영법으로 그린 지도다. 정각 도법이라는 특성상, 많은 웹지도가 유사 메르카토르 도법을 사용한다.
메르카토르 도법의 가장 큰 특징은 위도와 경도가 지도상에 평면좌표계의 X축과 Y축으로 나타난다는 점이다. 따라서, 메르카토르 도법은 두 지점사이의 직선이 위도 또는 경도와 이루는 '각'을 정확하게 보여준다. 대신에 면적, 거리, 방향은 보장할 수 없다. 적도 부근은 거의 정확하게 투영되지만, 고위도로 갈수록 간격이 실제보다 확대되면서 면적이나 형상이 크게 왜곡된다. 이는 실제 경선의 간격이 고위도로 갈수록 좁아지는 것에서 기인한 것으로, 고위도로 갈수록 실제에 비해 가로로 늘어나 길쭉하게 된다. 게다가 가로로만 늘어나는 게 아니라 위 그림에서 볼 수 있듯이 세로로도 늘어난다.
면적, 방향, 거리 등 요소들의 왜곡은 sec(위도)가 나타내며, 이 값과 1의 차이가 커질수록 왜곡은 커진다. sec(0) = sin(90) = cos(0) = 1이며, sec(90°)는 tan(90°)와 같은 무한대이므로 적도의 왜곡은 없고, 양 극점의 왜곡은 무한대다. 북극점과 남극점은 점이므로 수학적으로 크기가 0, 즉 길이도 지름도 없는데, 지도상에서는 적도에서의 지구 둘레와 똑같이 늘어난다. 즉, 0이 4만 킬로미터 이상으로 늘어나는 것이므로 왜곡률은 분모가 0으로 발산해서 생기는 무한대가 된다.
이러한 특징으로 인해 메르카토르 도법으로 그려진 지도는 출발점과 목적지를 직선으로 연결하고 이 직선과 위선 사이의 각을 재면 원하는 목적지에 정확히 갈 수 있다. 쉽게 이야기하면, 지도 위에 나침반 갖다 대고는 자기가 가고자 하는 방향이 북극과 이루는 각도를 계산한 후, 그 각도를 유지하며 나아가면 지도에 나와있는 대로 따라갈 수 있다는 이야기. 나침반이랑 각도기만 있으면 지도에 보이는 대로 항해할 수 있으니, 항해하기에 매우 편한 지도이다. 전문 용어로 말하자면 메르카토르 도법에서 두 점 사이의 직선은 항상 지구상에서 항정선에 해당한다. 이 루트는 당장 어느 방향으로 가야 목적지에 갈 수 있을 지 알아내는 데는 편리하다. 하지만 항정선이 반드시 최단 경로인 대권 항로가 되는 것은 아니다.
메르카토르 투영법이 남용되면서 많은 비판을 받았는데 주로 지목되는 것은 면적의 왜곡이다. 극 부분에 가까운 고위도 지역이, 적도와 가까운 저위도 지역보다 더 크고 자세하게 묘사된다. 사실 모든 도법에 오류가 있다는 점에서 부당한 면이 있다. 특히 왜곡이 심한 극지방의 경우 어차피 유빙한계선 때문에 항해가 불가능하여 관심이 적은 곳이기에 북위 65도, 남위 45도까지 그려진 지도면 충분한 점도 작용했다. 항해사 입장에서는 남극 대륙을 크게 그릴 것이 아니라 아예 남극을 안 그리면 그만인 것이었다.
문제점
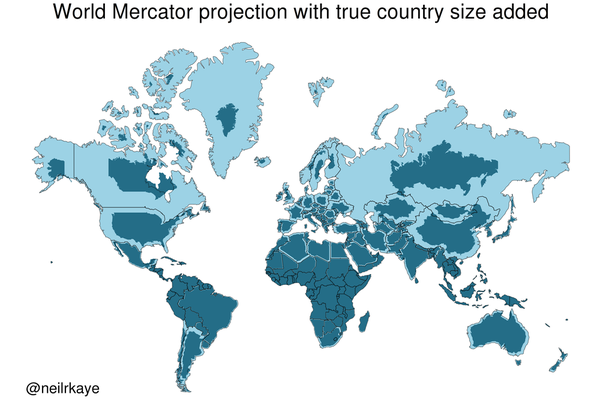
메르카토르 도법은 적도에서 먼 지역일수록 면적이 뻥튀기되기 때문에 수많은 오류가 나타난다. 이를 세계지도상에서 비교할 수 있는 사이트도 있다. 이에 따라 생기는 관념적인 오류의 예는 다음과 같다.
- 노바야 제믈랴가 일본과 사할린을 합한 크기로 보이지만 일본이 노바야 제믈랴보다 4배 이상 더 크다.
- 그린란드와 아프리카는 거의 같은 크기로 보이지만 실제로 아프리카 면적은 그린란드 면적의 14배이다. 게다가 실제로 그린란드는 아프리카에서 가장 넓은 나라 알제리보다 작다. 그리고 그린란드보다 큰 섬은 대륙으로 취급하므로 메르카토르 도법상에서 그린란드보다 훨씬 작아 보이는 호주가 대륙이라는 말을 듣고 갸우뚱한 적이 있을 것이다. 그러나 지구본으로 보면 간단히 해결되는 문제이다.
- 아프리카와 거의 같은 크기로 묘사되는 그린란드는 실제로는 아프리카는 커녕 호주보다 작고 아르헨티나보다도 작다. 정확히는 그린란드가 아르헨티나의 75%밖에 안 되는 면적이다.
- 캐나다와 아프리카는 면적이 비슷해 보이지만 실제로는 아프리카가 캐나다의 3.3배이고 러시아의 1.76배를 차지한다.
- 러시아가 남아메리카보다 3~4배 정도 더 커보이지만 실제로는 남아메리카가 약간 더 크다.
- 알래스카는 멕시코는 물론이고 수단이나 리비아보다 도 3배나 더 커보이지만 실제로는 알래스카가 이 셋보다 더 작다.
- 누나부트 준주는 멕시코보다 3~4배나 더 커 보이지만, 실제로는 멕시코가 더 크다.
- 아이슬란드는 한반도와 비슷한 크기로 보이지만 실제로는 남한 정도의 크기다. 실제로 위의 세계지도상 면적 비교 사이트에 가서 남한 영토와 면적이 비슷하고, 북한보다 작은 또 다른 국가 헝가리, 과테말라, 불가리아, 포르투갈, 요르단, 세르비아, 온두라스, 말라위, 에리트레아 가운데 하나를 정해서 아이슬란드 쪽으로 옮긴 뒤 회전시켜 보면 상당부분 겹친다.
- 캄차카 반도는 한반도보다 2배 이상 더 커 보이지만 실제론 한반도의 약 1.2배 크기다.
- 한반도가 라오스보다 약간 더 커 보이지만 실제로는 라오스가 약간 더 크다.
- 한반도 전체의 크기가 실제로는 영국 본토의 섬이나 가나와 비슷하다.
- 영국이 에콰도르보다 2배는 더 커보이지만 실제로는 에콰도르가 영국보다 약간 더 크다.
- 노르웨이가 터키보다 더 커 보이지만 실제로는 터키가 2배 정도 더 크며 노르웨이는 스발바르 제도를 합칠 경우 총 면적은 우즈베키스탄 보다 약간 작다.
- 일본은 핀란드보다 작아 보이지만 실제로는 핀란드보다 더 크다.
- 남극이 아시아를 제외한 다른 대륙을 다 합친 것 만큼 거대해진다.
- 오스트레일리아가 브라질보다 커 보이지만 실제로는 브라질이 더 크다.
- 콩고민주공화국은 서유럽의 절반 내지는 2/3 정도로 보이지만 실제로는 비슷한 수준이다.
- 독일이 마다가스카르나 보츠와나, 케냐보다 더 커 보이지만 실제로는 케냐가 더 크다. 그리고 보츠와나와 마다가스카르는 실제로 도서지역을 제외한 프랑스보다도 더 크다.
- 스페인과 볼리비아의 면적이 서로 비슷해 보이지만 실은 볼리비아가 2배 이상 더 크다.
- 프랑스는 콜롬비아와 비슷해 보이지만 실은 콜롬비아가 2배 이상 더 크다.
- 네덜란드, 덴마크(본토 한정), 에스토니아는 서로 면적이 비슷한 나라들로, 이들 셋이 도미니카 공화국보다 더 커 보이지만, 실제로는 도미니카 공화국이 1.14배 정도 더 크다.
- 슬로바키아, 보스니아가 코스타리카보다 2배 정도 가까이 큰 것처럼 보이지만, 실제로는 보스니아-헤르체고비나랑 코스타리카는 면적이 거의 비슷하며, 이쪽은 슬로바키아보다도 약간 더 크다.
- 리투아니아와 라트비아는 스리랑카보다 2배 이상 더 커 보이지만 실제로는 스리랑카가 라트비아보다 약간 더 크며 리투아니아와 거의 비슷한 크기이다. 마찬가지로 크로아티아도 토고보다 2배 이상 더 커 보이지만, 실제 이 둘의 면적은 거의 비슷하다.
- 벨라루스가 기니보다 커 보이지만 실제로는 기니가 약간 더 크다.
- 인도와 몽골은 얼핏 보면 비슷해보이지만 실제로는 인도가 몽골의 2배가 살짝 넘는다.(2.1배) 마찬가지로 몽골 옆에 있는 카자흐스탄이 인도보다 더 큰 것 같지만 사실 인도가 카자흐스탄의 1.19배 정도로 더 크다.
- 스웨덴이 우즈베키스탄, 파푸아뉴기니, 모로코 이렇게 셋보다 2배 이상 더 커보이지만 실제 이 네 나라 끼리의 면적은 거의 유사하다.
- 핀란드는 적도 부근의 콩고 공화국보다 2~3배 정도 더 커보이지만 실제로는 콩고 공화국이 약간 더 크다.
- 파나마가 코소보를 제외한 세르비아 본토보다 작아 보이지만 실제로는 파나마가 세르비아 본토보다 더 크다.
- 브라질이 알래스카를 제외한 미국 본토보다 작아 보이지만 실제로는 브라질이 미국 본토보다 더 크다.
- 아르헨티나가 인도보다 커 보이지만 실제로는 인도가 더 크다.
- 우간다는 사할린 섬과 면적이 거의 비슷해 보이지만 실제로는 우간다가 3배 정도 더 크며, 캄차카 반도가 우간다의 3배 정도로 커 보이지만 실제로는 약 1.14배 정도의 오차다.
- 우크라이나는 탄자니아와 넓이가 비슷하거나 더 커 보이지만 실제로는 탄자니아가 1.56배 정도 더 크다. 우크라이나와 북쪽의 벨라루스를 합쳐서 그 면적을 비교해 봐도 탄자니아가 1.19배 정도 더 크다.
- 미국의 위스콘신 주는 코트디부아르와 넓이가 비슷해 보이지만 실제로는 코트디부아르가 2.1배 정도 더 크다.
- 대한민국의 경상북도는 르완다보다 좀 커 보이지만 실제로는 르완다가 1.38배 정도 더 크다.
- 중국의 헤이룽장성은 중앙아프리카 공화국과 넓이가 비슷해 보이지만 실제로는 중앙아프리카 공화국이 1.37배 정도 더 크다.
- 프랑스의 넓이와 독일의 넓이가 비슷해 보이지만 사실 프랑스 유럽 본토의 면적이 독일(약 36만km²)의 1.5배인 약 54만km² 이다. 또한 스웨덴이 러시아를 제외 한 유럽내에서 가장 커보이지만 알고보면 45만km²로 프랑스보다 작다.
국가별로 영토 면적을 일일이 찾아보거나 직접 웹 사이트(구글, 인터넷, 네이버, 크롬, 다음 등)를 찾아보는 것도 좋겠지만, 영토 크기 자체를 정확하게 알려는 목적보다는 눈대중으로 비교하더라도 최대한 왜곡없이 비교하는 방법은 구형 지도, 즉 지구본을 보거나 구글 어스를 이용하는 것이다. 특히 해외 영토가 많은 나라이거나 다수의 섬으로 이루어진 나라의 경우 나라 전체의 영토가 아닌 특정 지역이나 섬의 영토를 비교할 수도 있으므로 단순 비교 목적이라면 정확한 면적 찾기가 귀찮아진다.
왜곡의 정도
앞에서도 말했 듯이 오른쪽 숫자가 1에서 벗어날수록 오차가 커지며, 이 숫자는 몇 배나 차이나는지를 말해 준다. 예를 들어 오른쪽 숫자가 2라면 그 위도에 있는 것은 실제보다 2배 크게 보인다는 뜻이다. 그리고 이것은 지구가 완벽한 구형임을 가정할 때의 결과이다. 여담으로, 이 수치는 n차원 단체의 이포각이 m°라고 했을 때, m°의 왜곡 정도의 n배와 정확히 같다. 즉, 위도가 m°일 때, n-단체의 이포각이 m°가 된다면 실제로 n이 차원의 수일 때, 정확히 n배 커진 것과 같다는 뜻이므로 이를 이용해서 n-단체의 이포각이 m°를 이루는 차원을 직접 구할 수 있다.
위도에 따른 왜곡의 정도 위도 왜곡의 정도 0° 정확히 1 10° 1.01542 20° 1.06418 24.62° 1.10000 30° 1.15470 38° 1.26902 40° 1.30541 45° 1.41421 48.19° 1.50000 50° 1.55572 60° 정확히 2 70° 2.92380 80° 5.75877 90° 무한대
참고로 많은 메르카토르 도법 지도는 남북위 85° 정도에서 잘리는데, 애초에 극점에서 일어나는 극단적 왜곡때문에 자를 수 밖에 없기도 하거니와, 저 부근에서 자르면 가로:세로 비율이 1:1이 되기 때문이다.
sec x dx 를 -85pi/180부터 +85pi/180까지 적분하면(적분의 위아래 끝은 육십분법을 라디안으로 바꾼 것) 약 6.26이 나오며 이 값은 원주율의 두 배(360도에 해당하는 라디안)와 비슷한 값이다. 즉 가로는 지구 전체의 경도이니 원주율의 두 배가 되며 세로도 비슷한 값이 되는 것이다. 지구가 완벽한 구형이라고 가정하면 적도에서는 위도 1도와 경도 1도의 실제 거리가 일치하는데, 고위도로 갈수록 경도 1도의 길이가 짧아지며, 메르카토르 도법에서는 경도가 짧아지는 비율만큼 위도를 부풀리므로 저 적분값의 시작과 끝을 0과 해당 위도(라디안으로 변환 후)로 잡아주고 그 결과값을 라디안으로 보고 육십분법으로 변환하면 경도 몇 배만큼 적도에서 멀어지나를 볼 수 있다. 가령 북위 35도라면 저 적분을 해보면 약 0.65284가 나오고 이것을 라디안으로 보고 육십분법으로 변환하면 37.405도가 나오는데, 지도상 해당 경도에 해당하는 적도의 점에서 경도 37.405도의 길이에 해당하는 만큼 북쪽으로 가서 찍어주면 된다는 소리다.
항정선과 대권의 차이
구면 위에서 두 점을 잇는 가장 짧은 거리, 즉 구면 위에서의 직선은 그 두 점을 잇고 중심이 구의 중심인 원의 일부분(호)이다. 이 원을 대원이라고 하는데, 지리학에서는 대권이라고 한다. 대권과 항정선은 평면에 익숙한 직관으로는 같을 것 같지만 실제로는 항정선이 더 길다. 이는 메르카토르 도법이 정거 도법이 아니라는 얘기기도 한데, 그래서 이런 일이 생긴다.
가장 대표적인 예시로 뉴질랜드 남단에서 칠레 남단까지의 직선거리(남태평양 경유)가 브루나이에서 소말리아 모가디슈까지의 직선거리보다 짧게는 1.5배에서 길게는 2배 정도 길어보이지만 실제로는 둘이 비슷한 수준이다.
메르카토르 도법을 기준으로 한 대항해시대 시리즈에서는 다른 문제를 보인다. 메르카토르 도법에선 '두 지점 간의 거리가 부정확하다'는 것. 남/북극 항로가 실제보다 엄청나게 길며, 이 때문에 별다른 페널티가 없어도 북극항로 탐험이 상당히 힘들다. 다만 대항해시대 3에서는 위 점을 보정하여 극지방으로 갈수록 경도 변화 속도가 빠르게 변한다. 그러므로 북극항로를 이용하면 빨리 갈 수 있는 셈. 농담이 아니라 대항해시대에는 북극항로와 남태평양 항로는 당시의 기술부족으로 무용지물이었고 호주의 존재도 늦게 알려졌다. 그래서 거리 부정확이 별로 문제가 안 된 것이다.
메르카토르 도법만의 문제가 아니다
메르카토르 도법은 범용성과 높은 인지도 때문에 그 왜곡된 면적에 관한 사실이 널리 알려져 있다. 다만 지구는 적도가 볼록한 구형체이기 때문에 전 지구를 평면 위에 왜곡 없이 나타내는 것은 불가능하다. 이는 카를 프리드리히 가우스가 수학적으로도 증명한 사실이다. 그러므로 메르카토르 도법만 부정확한 게 아니라, 전 지구를 평면 위에 표현하는 모든 도법은 부정확하게 그려진다.
심심하면 메르카토르 도법이 까이는 이유는, 일반인들의 지리 인식에서 가장 먼저 눈에 들어오고 비교하는 것은 영토와 영해의 크기이기 때문이다. 만약 이러한 용도로 지도를 보겠다면 정적 도법이 필요한데, 메르카토르 도법은 정각 도법, 그 중에서도 항해에 필요했던 항정선을 정확하게 보여주는 용도일 뿐 일반인이 직관적으로 지구의 모습을 이해하기 쉬우라고 만든 것이 아니라는 점이다. 사실 얘도 정각 도법, 그러니까 정형 도법인 만큼 나라 모양은 꽤 정확하게 보여주는 편이다. 하지만 대중은 지도를 보면서 면적을 상당히 중요하게 여기는데 메르카토르 도법은 면적이 많이 왜곡되기 때문에 심심하면 까이는 요소가 된다. 그래서 메르카토르 도법의 개선안으로 나오는 지도들은 정적 도법이거나, 그렇진 않더라도 모양과 면적 사이에서 적당히 타협한 절충 지도들이다.
하지만 어떤 의미로는 일반인들이 가장 선호하는 지도라고도 할 수 있다. 적도 쪽보다는 고위도 쪽에 상대적으로 영토가 작은 국가들이 많다. 세계지도를 잘 보면 브라질, 콩고민주공화국, 케냐, 인도네시아 네 나라가 육지에서 적도가 지나가는 곳을 대부분 가져가는 반면, 북위 40도 정도로 올라가면 지중해, 서아시아, 중앙아시아, 동북아시아를 지나 미국을 관통하며 남위 40도로 내려가면 칠레, 아르헨티나, 호주 남단과 뉴질랜드를 지나간다. 극지방으로 올가라면 심해지는 면적 왜곡이 이 점을 오히려 보정하여 중위도에 위치한 소국까지 작은 지도에도 가능한 생략 없이 온전하게 표현할 수 있게 해준다.
지도 자체가 사각형 형태라서 깔끔하게 액자나 틀에 꽂아넣기 좋다는 점도 크게 작용한다. 구드 호몰로사인 도법은 많은 나라가 몰린 남북위 40도에서 왜곡의 정도가 가장 적기에 영토를 주로 보는 대중 입장에서는 그나마 정확한 지도에 가깝지만, 바다를 반씩 갈라서 표현해 미관용 세계 지도로는 인기가 별로다. 다양한 도법이 발전하면서 로빈슨 도법같이 왜곡을 줄이면서도 미관상 사각 틀에 넣기 좋은 지도들도 많이 나왔다.
유럽 중심주의 음모론
이를 두고 메르카토르 도법이 유럽 중심 세계관을 반영한 것이라는 비판을 받기도 하는데 이는 근거가 빈약하며 낭설이다. 이 주장이 성립하려면 메르카토르 도법 이외의 대안이 있는데도 불구하고 굳이 메르카토르 도법을 고수하는 경우여야야 성립하는데 그런 것도 아니다.
앞서 설명했듯이 메르카토르 도법이 사용된 이유는 단순히 '항해에 편해서'이다. 메르카토르 도법상에서 두 지점을 이은 선분은 지구 경선에 대해 같은 각도를 유지하는 등각 항로가 되기 때문에, 항해 도중 방향을 고칠 때 별다른 보정 작업이 필요가 없다. 선박의 현재 위치로부터 목적지까지 이은 직선과 동일하게 뱃머리를 그 방향으로 바꾸기만 하면 그만이다.
역사적으로 특정 '도법'을 도입해야 할 정도의 소축척지도는 대부분 항해를 위해서 필요한 경우가 대부분이었다. 군사지도나 그 지역의 지형을 알아보는 정도의 대축척지도는 그냥 평면도로 제작해도 문제가 없었다. 반면 항해는 워낙 이동거리가 멀다보니 대축척으로는 올바른 경로를 찾기 힘들었고 자연스럽게 도법 자체도 항해에 최적화된 도법이 많이 쓰인 것이다. 즉, 역사적으로 다양한 형태의 도법을 이용한 지도들이 있었고, 다양한 이유로 사장되는 지도들이 있는 가운데 거기서 살아남은 것들 사이에서도 (지도를 사용하는)많은 사람들에게 채택되어 자연스럽게 현재까지 명맥을 잇게 된것이 메르카토르 도법인 것이지, 누군가가 임의로 이것을 정식으로 지정한 것이 아니다.
따라서 항해를 위해 메르카토르 도법 지도를 제작하고 보니 단지 우연히 유럽이 고위도 지역에 있었기 때문에 크고 자세하게 묘사되는 이득(?)을 얻은 것처럼 보이는 것 뿐이다. 물론 '만약 면적의 이득을 보는 쪽이 미국과 유럽이 아니라 아프리카나 아시아였다면 서구 선진국들이 그것을 가만히 수긍했을까?' 정도의 생각은 들 수 있고, 이를 근거랍시고 음모론을 정당화하려는 사람이 많다. 당연히 이는 존재하지 않은 일에 대한 가정이기에 말그대로 가정은 할 수 있을 지언정 그 가정을 확신할 현실적인 근거는 어디에도 없다.
애초에 메르카토르 도법으로 가장 이득을 본 지역이 유럽인 것도 아니다. 위의 보정 지도들을 보면 알겠지만, 메르카토르 도법의 가장 큰 수혜자는 러시아, 그린란드, 캐나다 등 극지방 국가들이다. 만약 정말로 유럽이 자기네들을 크고 웅장하게 보이고 싶은 목적으로 특정 도법을 전세계에 '강요'했다면 상대적으로 변방이나 다름없는 이 나라들이 아니라 유럽 주요국들이 몰려있는 중위도 지방이 가장 커보이는 도법을 썼을 것이다.
갈-페터스 도법
실제로 이런 주장을 바탕으로 방향에 대한 정확성은 포기하고 정확한 면적을 표현하기 위해 만들어진 갈-페터스 도법이 존재한다. 그러나 갈-페터스를 신봉하는 일부 몰지각한 사람들이 "메르카토르 도법은 서양 중심의 제국주의 도법이다!"라고 언플하여 지리학자나 전문가들에게 매우 까이고 있다.
미국이 냉전 시절에 메르카토르 도법을 이용했다는 이야기도 있다. 소련이 원래 땅이 넓기도 했지만 미국보다 더 북쪽에 있었으므로 면적의 왜곡이 훨씬 커져서 미국보다 엄청나게 크게 보였던 것. 따라서 소련의 위협을 지도를 보고 실감토록 했다는 것. 헛소리라고 듣고 넘기면 된다.
등장방형도법
또한 위도와 경도가 1:1로 나온 지도인 등장방형도법도 있어 보인다. 이경우에도 메르카토르 도법보다 왜곡은 좀 덜하되 위도는 왜곡이 없지만 고위도로 갈수록 경도에는 왜곡이 생긴다. 기상계에서 종종 쓰이는 경우가 있다.
동영상
참고자료
- 〈메르카토르 도법〉, 《나무위키》
- 〈메르카토르 도법〉, 《위키백과》
- 〈그리는 방법에 따라 달라지는 지도의 모양〉, 《에듀넷》
같이 보기
| ||||||||||||||||||

 위키원
위키원