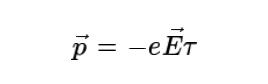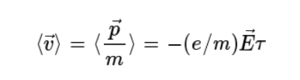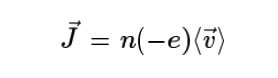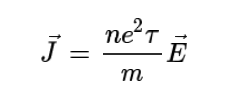"자유전자"의 두 판 사이의 차이
잔글 (→개요) |
잔글 (→같이 보기) |
||
| (같은 사용자의 중간 판 하나는 보이지 않습니다) | |||
| 59번째 줄: | 59번째 줄: | ||
== 같이 보기 == | == 같이 보기 == | ||
| + | * [[자유]] | ||
* [[전자]] | * [[전자]] | ||
| + | * [[원자]] | ||
| + | * [[원자핵]] | ||
| + | * [[궤도]] | ||
* [[전기장]] | * [[전기장]] | ||
* [[자기장]] | * [[자기장]] | ||
* [[자유전자모형]] | * [[자유전자모형]] | ||
| − | {{ | + | {{전기|검토 필요}} |
| + | {{화학}} | ||
2024년 10월 29일 (화) 00:56 기준 최신판
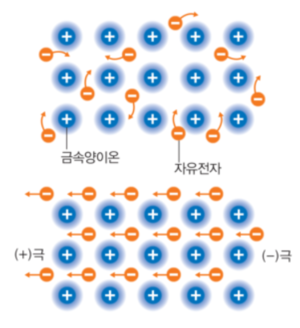
자유전자(free electron)는 원자로부터 해방되어 자유롭게 돌아다닐 수 있는 전자이다. 따라서 균일한 전기장이나 자기장 이외에 외부로부터 힘을 받는 일 없이 자유로이 움직인다. 원자 1개 속에는 원자번호와 같은 수의 전자가 있는데 대부분은 원자핵과의 전기적 작용에 의해 원자 안에 묶여 있다. 원자가 모여서 금속이 되면 원자 사이의 상호작용에 의해 각 원자의 가장 바깥쪽에 있는 전자가 해방되어 금속 안을 돌아다니는 자유전자가 된다.
금속이 전기나 열을 전하기 쉬운 것은 자유전자가 전하나 열운동의 에너지를 운반하기 때문이다. 반도체에서는 불순물 원자의 둘레에 느슨하게 묶여 있는 전자가 열운동에 의해 해방되어 자유전자가 된다. 열전자관이나 브라운관 등의 전자관은 음극에서 방출된 자유전자의 운동을 제어해 이용하는 것이다.또 대기 상층의 전리층에는 자유전자가 자연으로 존재해 전파반사의 원인이 된다.
물질 속의 자유전자라는 개념은 20세기초에 독일의 P.K.L.드루데와 H.A.로렌츠에 의해 금속의 원자가전자(原子價電子)가 자유전자의 기제로서 존재한다고 가정하면 금속의 전기전도·열전도 및 광학적 성질 등을 대략 섣명할 수 있다는 데서 형성되었다. 이것을 고전 자유전자모형이라고 하는데, 금속의 전기전도도(電氣傳導度)와 열전도도의 비는 같은 온도에서는 금속의 종류에 상관없이 같은 값을 가진다는 비데만-프란츠의 법칙을 설명할 수 있다. 그러나 고전적인 모형으로는 금속의 비열이나 상자성 대자율(常磁性帶磁率) 등에 대해서는 실험과 모순되고, 전자가 왜 격자간격(格子間隔)의 수백배의 거리를 마치 진공속에 있는 것과 같이 자유로이 운동할 수 있는냐 하는 점도 설명할 수 없다.
원자·분자 등의 내부에 속박되어 자유로이 운동할 수 없는 전자는 속박전자(구속전자)라고한다.
현재는 양자역학에 의거한 밴드이론에 의해 금속의 자유전자모형의 기초설정이 이루어지고 있다.
개요[편집]
자유전자는 도체 물질에 대한 모형에서 상호작용이 없이 자유롭게 움직일 수 있다고 가정한 전자들이다. 금속 원자들이 금속결합을 하며 고체를 이룰 때 각 원자에서 떨어져 나온 원자가전자를 자유전자로 근사할 수 있다.
고전적인 드루드 모형(Drude model)에서 원자가전자는 원자로부터 완전히 떨어져 나와 자유롭게 움직이는 전자 기체를 형성한다. 이 기체는 이상기체로 취급될 수 있다. 즉, 전자와 전자 사이의 상호작용은 완전히 무시된다. 이온이 된 원자에 의한 전기장은 스크린 효과에 의해 미약하다고 가정한다.
드루드 모형은 옴의 법칙을 설명하는데 유용하다. 외부의 전기장이 없는 경우, 전자들은 열적 효과에 의해 무작위로 움직인다. 이러한 무작위 운동의 평균속도는 당연히 0이다. 전기장이 가해지면 각각의 전자는 힘을 받고 가속r라면 전기장 E→에 의한 -e의 전하량을 가진 전자의 운동량의 변화량은
이다. 그러므로 전자의 평균속도는 더 이상 0이 아니고
이 된다. 이것을 유동 속도(drift velocity)라고 한다. 전류밀도 J→는 자유 전자의 개수 밀도가 n일 때
와 같이 유동 속도에 비례한다. 따라서
와 같이 전류밀도가 전기장에 비례함을 알 수 있다. 이것은 옴의 법칙 V = IR의 또 다른 표현이기도 하다. 이때 비례상수를 전기전도도 σ라 한다. 드루드 모형에서는 전기전도도가
σ = ne²T/m
로 구해진다.
금속결합에 의한 자유전자[편집]
원자모형은 양파껍질처럼 서로 떨어진 껍질들이 있고 한 껍질내의 전자들은 같은 에너지를 갖는다고 설명한다. 그런데 각 껍질 내에 들어갈 수 있는 전자의 수는 정해져 있어 안쪽으로부터 2, 8, 8. 18. 18, 32 등이 된다. 원자핵에서 멀어질수록 전자의 에너지는 높고 원자핵의 인력은 작아진다.
금속결합이란 금속의 양이온과 자유전자 사이에 정전기적 인력(쿨롱의 힘)에 의해 이루어진 결합이다. 금속결합에서 원자내 전자들이 위치하는 껍질들이 다른 원자들의 껍질과 겹쳐 전자들이 위치하는 띠를 형성하게 된다. 원자가 전자들은 가전자대(valence band)에 위치하게 된다. 금속 내에서 자유로이 움직일 수 있는 에너지띠를 전도대(conduction band)라고 한다. 이 전도대에 있는 전자들을 여러 원자핵들이 공유하게 되어 개별적인 원자핵의 인력으로부터 자유롭게 된다. 가전자대에는 원자 안쪽의 궤도들이 서로 겹치면서 만들어진 것으로 연속적인 에너지를 가지는 전자들이 모(母)원자 주위에 구속된 채로 다른 곳으로 이동을 할 수가 없는 곳이다. 이에 반해, 전도대는 원자 바깥쪽의 궤도들이 겹치면서 만들어진 것으로 연속적인 에너지를 가진 전자들이 이 원자 주변에서 저 원자 주변으로 자유롭게 이동할 수 있는 곳으로, 이 전도대에 올라와 있는 전자를 자유전자라고 한다.
도체란, 가전자대와 전도대의 에너지 격차가 아주 작거나 서로 겹쳐 있어서 평상시에도 전도대에 다수의 전자가 존재하는 물질을 말하며, 부도체란 이 에너지 격차가 너무 커서 가전자대의 전자가 전도대로 오르지 못하는 물질이다. 금속결합은 원자가 전자가 1~2개여서 안정된 전자배열이 되기에 전자를 내버리는 쪽이 수월한 원자들이 서로 가전자대에 가깝거나 겹치게 전도대를 형성하여 전자를 서로 공유하므로 자유전자가 생긴다. 자유전자수가 많을수록 금속의 결합력은 커지게 된다. 이렇게 생긴 금속 내 자유전자는 다른 입자와의 상호작용으로 에너지를 얻어 금속을 빠져 나가게 될 때까지 금속 내에서 자유로이 움직이게 된다.
전리층에서 자유전자[편집]
전리층은 고도 약 60km~400km에 이르는 구간에 있다. 대양에서 복사된 자외선, 대전된 미립자 등과 우주에서 입사되는 우주선이 질소나 산소원자와 충돌하고 이 충돌에 의한 에너지로 전자가 방출되면서 양이온이 된다. 이러한 전리작용에 의해 자유전자와 양이온이 형성된다. 이 전리층에 의해 지상으로부터의 전파가 반사되기도 한다.
자유전자와 열전도와 관계[편집]
보통의 물질의 경우 열에너지는 순전히 분자들끼리 진동하면서 전해진다. 예를 들어 알갱이들이 서로 뭉쳐 있는 상태라고 한다면, 그 가운데 하나가 떨리면 그 떨림이 옆 알갱이에 전파되고, 그 전파된 알갱이는 또 전파하는 식으로 진동이 전체로 퍼지게 된다. 하지만 금속은 자유전자가 어디든 이동할 수 있는 구조여서 열에 대한 효과적인 전파자의 역할을 한다. 금속은 열전도율이 좋게 된다.
자유전자모형 이론[편집]
아놀드 섬머펠트(Arnold Sommerfeld)에 의해 개발된 이론이다. 고체물리학에서 이 이론은 고전 드루드 모형(classical drude model)과 양자역학적 페르미-디락 통계를 통합하여 만들었다. 이 이론으로써 전기 전도성, 열 전도성, 열용량에 관한 온도 의존성, 전자의 상태밀도, 결합에너지 범위 등을 설명한다.
참고자료[편집]
- 〈자유전자〉, 《물리학백과》
- 〈자유전자〉, 《두산백과》
- 〈자유전자〉, 《사이언스올》
- 권상희 기자, 〈자유전자(free electron)〉, 《전자신문》, 2001-11-10
같이 보기[편집]
| ||||||||||||||||||||||

 위키원
위키원