"위치"의 두 판 사이의 차이
(새 문서: '''위치'''(Position)는 물체가 놓여있는 장소를 의미하는 공간 개념이다. 위치는 추상적인 개념이지만, 좌표계를 도입함으로써 이를 계량...) |
잔글 (→같이 보기) |
||
| (사용자 2명의 중간 판 3개는 보이지 않습니다) | |||
| 4번째 줄: | 4번째 줄: | ||
== 기준틀과 좌표계 == | == 기준틀과 좌표계 == | ||
| + | [[파일:평면직각좌표계.png|썸네일|300픽셀|그림1 평면 직각좌표계. 두 개의 파란 점의 좌표가 각각 (2, 3)과 (-3, -2)로 표시되어 있다. 붉은 점으로 표시된 원점의 좌표는 (0, 0)이다.]] | ||
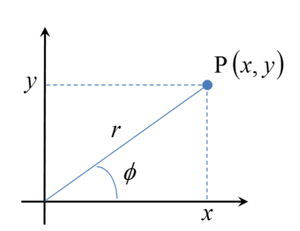
| + | [[파일:극좌표와 직각좌표의 관계.png|썸네일|300픽셀|그림2 극좌표와 직각좌표의 관계]] | ||
기준틀은 물체의 위치와 운동을 측정하는 표준을 제공하는데, 추상적 개념인 좌표계와 좌표계의 위치와 방향을 유일하게 고정하는 일련의 물리적인 기준점들로 구성된다. | 기준틀은 물체의 위치와 운동을 측정하는 표준을 제공하는데, 추상적 개념인 좌표계와 좌표계의 위치와 방향을 유일하게 고정하는 일련의 물리적인 기준점들로 구성된다. | ||
| 11번째 줄: | 13번째 줄: | ||
=== 직각좌표계 === | === 직각좌표계 === | ||
| − | + | 이차원 직각좌표는 평면에 놓인 임의의 점의 위치를 나타내는 좌표의 순서쌍이다. 이차원 직각좌표계는 두 개의 좌표축을 사용한다.(그림 1의 축과 축) 각각의 좌표축은 좌표를 표시하기 위한 기준선으로 방향성이 있는 직선이며, 서로 수직으로 교차한다. 두 개의 좌표축이 교차하는 위치를 통상 원점이라고 부르며 그 좌표는 (0,0)으로 나타낸다. 각 좌표는 상대 좌표축으로부터 점까지의 거리로 주어지는데, 이때 거리는 원점을 기준으로 [[양]](+) 또는 [[음]](-)의 부호를 갖는다. 한편, 좌표를 나타낼 점을 한 좌표축에 수직으로 투영했을 때 해당 좌표축 상에서의 위치를 그 점의 좌표로 정의하는 방법도 있다. 고차원 공간에서도 위와 같은 방법들을 확장하여 직각좌표를 정의한다. | |
| − | 이차원 직각좌표는 평면에 놓인 임의의 점의 위치를 나타내는 좌표의 순서쌍이다. 이차원 직각좌표계는 두 개의 좌표축을 사용한다.(그림 1의 축과 축) 각각의 좌표축은 좌표를 표시하기 위한 기준선으로 방향성이 있는 직선이며, 서로 수직으로 교차한다. 두 개의 좌표축이 교차하는 위치를 통상 원점이라고 부르며 그 좌표는 (0,0)으로 나타낸다. 각 좌표는 상대 좌표축으로부터 점까지의 거리로 주어지는데, 이때 거리는 원점을 기준으로 양(+) 또는 음(-)의 부호를 갖는다. 한편, 좌표를 나타낼 점을 한 좌표축에 수직으로 투영했을 때 해당 좌표축 상에서의 위치를 그 점의 좌표로 정의하는 방법도 있다. 고차원 공간에서도 위와 같은 방법들을 확장하여 직각좌표를 정의한다. | ||
=== 극좌표계 === | === 극좌표계 === | ||
| − | |||
'극(pole)'이라고 불리는 기준점은 직각좌표계에서의 원점과 유사한 역할을 한다. 극으로부터 기준 방향으로 뻗는 살(ray)을 '극선(polar axis)'이라 부른다.(그림 2에서는 x축) 임의의 점에 대해, 극으로부터의 거리를 '지름 좌표(radial coordinate)', 혹은 '반지름(radius)'이라고 부르고, 극선으로부터 임의 점까지 회전각의 크기를 '각 좌표(angular coordinate)', '극각(polar angle)', 혹은 '방위각(azimuth)'이라고 부른다. 지름 좌표와 각 좌표의 결합으로 주어진 좌표 (r,ϕ) 를 임의 점의 극좌표라고 부른다. 이와 같이 극좌표계는, 이차원 평면에서의 임의의 점의 위치가 기준점으로부터의 거리와 기준 방향에 대한 회전각에 의해 주어지는 이차원 좌표계이다. 다른 좌표계는 동일한 위치를 나타내는 다른 표현이기 때문에 서로 다른 좌표계의 좌표값 사이에는 변환식이 존재한다. 이를 [[좌표변환식]]이라고 한다. | '극(pole)'이라고 불리는 기준점은 직각좌표계에서의 원점과 유사한 역할을 한다. 극으로부터 기준 방향으로 뻗는 살(ray)을 '극선(polar axis)'이라 부른다.(그림 2에서는 x축) 임의의 점에 대해, 극으로부터의 거리를 '지름 좌표(radial coordinate)', 혹은 '반지름(radius)'이라고 부르고, 극선으로부터 임의 점까지 회전각의 크기를 '각 좌표(angular coordinate)', '극각(polar angle)', 혹은 '방위각(azimuth)'이라고 부른다. 지름 좌표와 각 좌표의 결합으로 주어진 좌표 (r,ϕ) 를 임의 점의 극좌표라고 부른다. 이와 같이 극좌표계는, 이차원 평면에서의 임의의 점의 위치가 기준점으로부터의 거리와 기준 방향에 대한 회전각에 의해 주어지는 이차원 좌표계이다. 다른 좌표계는 동일한 위치를 나타내는 다른 표현이기 때문에 서로 다른 좌표계의 좌표값 사이에는 변환식이 존재한다. 이를 [[좌표변환식]]이라고 한다. | ||
| 24번째 줄: | 24번째 줄: | ||
* [[좌표계]] | * [[좌표계]] | ||
* [[벡터량]] | * [[벡터량]] | ||
| + | * [[장소]] | ||
| + | * [[지도]] | ||
| − | {{ | + | {{물리|검토 필요}} |
2022년 5월 22일 (일) 20:19 기준 최신판
위치(Position)는 물체가 놓여있는 장소를 의미하는 공간 개념이다. 위치는 추상적인 개념이지만, 좌표계를 도입함으로써 이를 계량화할 수 있고 대수적으로도 다룰 수 있다. 수학적으로 위치는 좌표계의 원점으로부터의 거리와 방향에 의해 특정화되는 벡터량이다.
물체는 크기를 가지며 여러 부분으로 구성된다. 따라서 실제로 부분들의 위치는 각각 다를 수 밖에 없기 때문에 물체의 위치가 어느 곳이라고 말하는 것은 모호성이 있다고 할 수 있다. 그럼에도 불구하고 물체의 위치를 지정하여 말할 때는 대개 정확성을 무시하고 지정하거나, 혹은 물체의 크기를 무시하고 대신 물체의 위치를 대표하는 한 점의 위치를 지정하는 것이라고 할 수 있다. 점은 길이, 면적, 부피 등의 차원적인 속성을 갖지 않으며, 기하학에서는 공간을 구성하는 원초적인 객체이다. 물리학에서 물체의 병진운동을 다루는 경우가 바로 후자의 경우라고 할 수 있다. 이때 대표점은 물체의 질량중심이다. 질량중심은 크기를 갖지는 않지만 물체의 질량을 속성으로 유지하기 때문에 질량을 갖는 점, 즉 질점이라고 부른다.
기준틀과 좌표계[편집]
기준틀은 물체의 위치와 운동을 측정하는 표준을 제공하는데, 추상적 개념인 좌표계와 좌표계의 위치와 방향을 유일하게 고정하는 일련의 물리적인 기준점들로 구성된다.
n 차원 공간에서 기준틀을 정의하기 위해서는 n+1 개의 기준점을 정하는 것으로 충분하다. 예컨대 직각좌표계의 경우, 이 기준점들은 원점과 n개의 좌표축 위에서 원점으로부터 단위 거리만큼 떨어진 n 개의 점들로 구성된다.
좌표계는 물체의 위치를 표현하기 위한 수학적인 개념이자 언어이다. 자신의 관측을 기술하기 위해 관측자는 필요에 따라 다양한 좌표계를 선택할 수 있다. 예컨대, 관측 대상의 대칭성에 따라 직각좌표계나, 혹은 극좌표계 등을 선택할 수 있다. 하지만 다른 좌표계를 사용한다고 해서 물체의 위치가 달라지는 것이 아니며, 따라서 기준틀 자체가 달라지는 것은 아니다. 이것은 어떤 기준틀에 선호되는 특정한 좌표계가 존재하는 것은 아니라는 것을 의미한다. 여기서는 이차원 공간에 국한하여 가장 많이 사용되는 대표적인 좌표계인 직각좌표계와 극좌표계를 소개하겠다.
직각좌표계[편집]
이차원 직각좌표는 평면에 놓인 임의의 점의 위치를 나타내는 좌표의 순서쌍이다. 이차원 직각좌표계는 두 개의 좌표축을 사용한다.(그림 1의 축과 축) 각각의 좌표축은 좌표를 표시하기 위한 기준선으로 방향성이 있는 직선이며, 서로 수직으로 교차한다. 두 개의 좌표축이 교차하는 위치를 통상 원점이라고 부르며 그 좌표는 (0,0)으로 나타낸다. 각 좌표는 상대 좌표축으로부터 점까지의 거리로 주어지는데, 이때 거리는 원점을 기준으로 양(+) 또는 음(-)의 부호를 갖는다. 한편, 좌표를 나타낼 점을 한 좌표축에 수직으로 투영했을 때 해당 좌표축 상에서의 위치를 그 점의 좌표로 정의하는 방법도 있다. 고차원 공간에서도 위와 같은 방법들을 확장하여 직각좌표를 정의한다.
극좌표계[편집]
'극(pole)'이라고 불리는 기준점은 직각좌표계에서의 원점과 유사한 역할을 한다. 극으로부터 기준 방향으로 뻗는 살(ray)을 '극선(polar axis)'이라 부른다.(그림 2에서는 x축) 임의의 점에 대해, 극으로부터의 거리를 '지름 좌표(radial coordinate)', 혹은 '반지름(radius)'이라고 부르고, 극선으로부터 임의 점까지 회전각의 크기를 '각 좌표(angular coordinate)', '극각(polar angle)', 혹은 '방위각(azimuth)'이라고 부른다. 지름 좌표와 각 좌표의 결합으로 주어진 좌표 (r,ϕ) 를 임의 점의 극좌표라고 부른다. 이와 같이 극좌표계는, 이차원 평면에서의 임의의 점의 위치가 기준점으로부터의 거리와 기준 방향에 대한 회전각에 의해 주어지는 이차원 좌표계이다. 다른 좌표계는 동일한 위치를 나타내는 다른 표현이기 때문에 서로 다른 좌표계의 좌표값 사이에는 변환식이 존재한다. 이를 좌표변환식이라고 한다.
참고자료[편집]
- 〈위치〉, 《물리학백과》
같이 보기[편집]
| ||||||||||||||||||||||||||||||

 위키원
위키원