좌표계
좌표계(座標系, coordinate reference system, CRS)는 좌표의 종류, 원점, 좌표축 따위를 통틀어 이르는 말이다. 또는 지구 표면에 여러 줄의 위도선과 자오선을 그어 특정한 점의 위치를 나타낼 수 있도록 한 가상의 격자선을 말한다. 자리표계라고도 한다.
목차
[숨기기]개요[편집]
좌표계는 기하학에서 숫자나 기호를 써서 위치를 표기하는 방식을 뜻한다. 이 때의 위치를 지정하는 숫자나 기호는 좌표라 불린다. 필요에 따라 무수히 많은 임의의 좌표계를 만들 수 있으나, 과학에서 크게 유용한 2차원 좌표계는 두 가지, 3차원에서는 가장 유명한 세 가지이며, 각각의 특성이 있어서 용도에 적합한 것이 사용되곤 한다. 또한, 좌표계는 유클리드 공간과 같은 다양체의 점이나 기타 기하학적 요소를 고유하게 결정하기 위해 하나 이상의 숫자인 좌표를 사용하는 체계이다.
스칼라 튜플을 이용해 n차원 공간의 각 지점을 표현하는 방법을 말한다. 여기서 스칼라는 보통 실수, 경우에 따라서는 복소수나 다른 일반적인 환(ring)의 원소를 말하기도 한다. 복잡한 우주에서 스칼라는 우주 전체에 대해 효과적인 좌표계를 산출하지 못하기도 한다. 좌표를 나타내는 방법 중 하나인 데카르트 좌표계는 프랑스의 철학자이자 수학자인 르네 데카르트가 발명했다. 그는 천장에 붙어 있는 파리의 위치를 나타내는 방법에 대해 고민하다가 데카르트 좌표계를 발명해 냈다고 한다.
한국 교육과정상, 여기서 열거된 좌표계 중 데카르트 좌표계를 제외한 나머지(극좌표계, 원통좌표계, 구면좌표계)는 대학 미적분학, 공업수학, 전자기학에서 배운다. 그리고 복소평면은 전기전자공학과에서 페이저를 이용하여 교류 전원 회로를 분석할 때 사용한다. 좌표축의 정의역이 양의 실수 전체의 집합일 경우 로그 스케일 적용이 가능하다.[1][2]
대표적인 좌표계[편집]
기하학적 객체의 좌표[편집]
좌표계는 점의 위치를 지정하는 데 자주 사용되지만 선, 평면, 원 또는 구와 같은 더 복잡한 도형의 위치를 지정하는 데에도 사용될 수 있다. 예를 들어, 플러커 좌표는 공간에서 선의 위치를 결정하는 데 사용된다. 필요한 경우 설명되는 그림의 유형은 좌표계의 유형을 구별하는 데 사용된다. 예를 들어 선 좌표라는 용어는 선의 위치를 지정하는 모든 좌표계에 사용된다.
두 개의 서로 다른 기하학적 도형 세트에 대한 좌표계가 분석 측면에서 동일할 수 있다. 이에 대한 예는 투영 평면의 점과 선에 대한 동차 좌표계이다. 이와 같은 경우의 두 시스템은 이원적이라고 한다. 이원론적 시스템은 한 시스템의 결과가 다른 시스템으로 전달될 수 있는 특성을 가지고 있다. 왜냐하면 이러한 결과는 동일한 분석 결과에 대한 서로 다른 해석일 뿐이기 때문이다. 이것이 쌍대성의 원리로 알려져 있다.[1]
특징 및 종류[편집]
좌표계는 그 후 GIS에 저장된 2차원의 투영된 맵이 어떻게 지구상의 실재 위치에 연결되는지를 정의한다. 어떤 맵 투영법과 좌표계를 사용할지는 여러분이 작업하고자 하는 영역의 지역적 범위, 여러분이 분석하고자 하는 대상, 마지막으로 어떤 데이터를 사용할 수 있는지에 따라 결정한다. 좌표계 덕분에 지구상의 모든 위치를 좌표라는 숫자 3개 집합으로 지정할 수 있게 되었다. 일반적으로 좌표계를 크게 (데카르트 좌표계 또는 직교 좌표계라고도 하는) 투영 좌표계와 지리 좌표계로 나눌 수 있다.
지리 좌표계[편집]
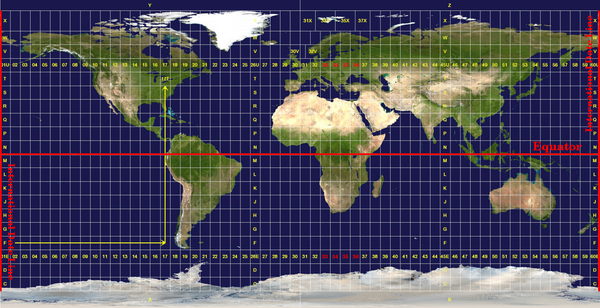
지리 좌표계(geographic coordinate reference system)는 매우 흔히 사용된다. 이 좌표계는 위도(latitude)와 경도(longitude) 그리고 때로는 고도 값을 사용해서 지구 표면상의 위치를 나타낸다. 가장 유명한 지리 좌표계는 WGS 84라고 한다. 위도선(line of latitude)은 지구를 북에서 남으로 (또는 남에서 북으로) 적도에 평행하게 균등한 간격으로 180개로 나누는 선입니다. 위도의 기준선은 적도이며 각 반구(hemisphere)를 90개로 나눕니다. 각 위도선은 위도 1°를 표현합니다. 북반구에서는 위도를 적도 0°부터 북극 90°로 측정합니다. 남반구의 경우 적도 0°부터 남극 90°로 측정합니다. 지도 디지타이즈 작업을 단순하게 하기 위해 남반구의 위도를 음수(0°에서 -90°)로 할당하는 경우가 많다. 지구 표면 어디에 있든, 위도선 사이의 거리는 60해리(海里)로 동일하다.
한편 경도선(line of longitude)은 위도선만큼 균등성 기준을 만족시키지 못한다. 경도선은 적도와 직교하며 남북극을 통과한다. 경도의 기준선(본초 자오선)은 북극에서 시작하여 영국 그리니치시를 통과해서 남극에서 끝난다. 그 다음 경도선들은 본초 자오선의 동쪽 또는 서쪽으로 0°에서 180°까지 측정한다. 본초 자오선 서쪽의 값은 디지털 매핑 응용 프로그램에서 사용할 수 있기 위해 음수로 할당된다는 사실을 기억한다. 적도에서, 그리고 적도에서만, 경도선 하나가 표현하는 거리가 위도 1°가 표현하는 거리와 동일하다. 남북극으로 이동할수록 경도선 사이의 거리는 점진적으로 짧아지는데, 양극의 정확한 위치에서 모든 360° 경도는 여러분의 손가락 끝으로 찍을 수 있는 한 점으로 모인다. 지리 좌표계를 사용하면 적도에서 약 12363.365km² 면적의 정사각형으로 지구를 분할하는 격자를 얻을 수 있다. 이것도 괜찮기는 하지만, 이 정사각형 안에 있는 객체의 위치를 구하기엔 쓸모가 별로 없는 것도 사실이다.
맵 상의 한 포인트의 위치를 (합당한 정확도 수준으로) 설명할 수 있으려면 맵 격자를 충분히 작은 부분들로 나누어야만 한다. 도(°)를 분 (')과 초 (")로 나누는 것입니다. 1도는 60분이며 1분은 60초다. (1도가 3,600초인 것이죠.) 즉 적도 상에서 위도 또는 경도의 1초는 30.87624m가 된다.
투영 좌표계[편집]
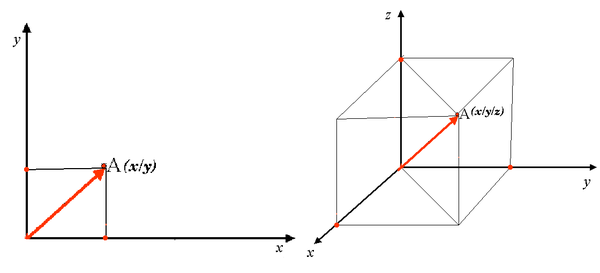
2차원 좌표계는 흔히 2개의 축으로 정의된다. 서로 직교하는 2개의 축은 XY 평면을 구성한다. 일반적으로 수평축을 X, 수직축을 Y라고 한다. 3차원 좌표계의 경우, 일반적으로 Z라고 하는 또 다른 축이 추가된다. 이 축도 X와 Y 축과 직교하며 Z 축은 3차원 공간을 생성한다. 구형 공간의 좌표로 표현된 모든 포인트는 X, Y, Z 좌표로 표현될 수 있다.
남반구(적도의 남쪽)의 투영 좌표계(projected coordinate reference system)는 일반적으로 적도 상의 특정 경도 를 원점으로 삼는다. 쉽게 말하자면 남반구에서는 Y값이 남쪽으로 갈수록 증가하고 X값은 서쪽으로 갈수록 증가한다는 뜻이다. 북반구(적도의 북쪽)의 경우에도 원점은 적도 상의 특정 경도 지만, Y값은 북쪽으로 갈수록 X값은 동쪽으로 갈수록 증가한다.
UTM 좌표계[편집]
UTM(Universal Transverse Mercator) 좌표계의 원점은 적도 상의 특정 경도이다. 이때 Y값은 남쪽으로 갈수록 증가하고 X값은 서쪽으로 갈수록 증가한다. UTM 좌표계는 전세계 맵 투영법이다.
그림을 보면 알 수 있듯이 남아프리카 공화국은 왜곡을 최소화하기 위한 4개의 UTM 구역 으로 덮여 있다. 이 구역들 은 UTM 33S, UTM 34S, UTM 35S 그리고 UTM 36S이다. 구역 번호 뒤에 붙은 S는 해당 UTM 구역이 남반구에 있다는 의미이다. 관심 지역(AOI) 내에 있는 2차원 좌표를 정의하려 한다고 하면 해당 지역은 UTM 구역 35S에 위치하고 있다. 즉 왜곡을 최소화하고 정확한 분석 결과를 얻기 위해서는 좌표계로 UTM 구역 35S를 사용해야 한다.
남반구 UTM 좌표의 위치는 구역 번호 (35)와 미터 단위의 편북(Y) 값 그리고 편동(X) 값 으로 표현해야만 한다. 편북(northing) 값이란 적도 에서부터 해당 위치까지의 거리를 미터 단위로 나타낸 값이다. 편동(easting) 값은 사용된 UTM 구역의 중심 자오선 (경도)에서부터 해당 위치까지의 거리를 미터 단위로 나타낸 값이다. UTM 구역 35S의 경우 중심 경도는 동경 27도이며 더 자세히 설명하자면 지금 남반구를 설명하고 있는데 UTM 좌표계에서는 음수를 사용할 수 없기 때문에 편북(Y) 값에 가짜 편북 값(false northing value) 10,000,000m를 더해주고 편동(X) 값에 가짜 편동 값 500,000m를 더해줘야 한다. 어려운 것 같으면 관심 지역의 정확한 UTM 35S 좌표를 찾는 방법을 보여주는 예제를 풀어봐야 한다.
- 편북(Y) 값 : 우리가 찾는 위치는 적도에서 남쪽으로 3,550,000m 거리이므로 편북(Y) 값은 음의 부호이며 -3,550,000m가 되는데, UTM 정의에 따라 가짜 편북 값 10,000,000m를 더해야 한다. 따라서 해당 위치 좌표의 편북(Y) 값은 6,450,000m(-3,550,000m + 10,000,000m)이다.
- 편동(X) 값 : 먼저 UTM 구역 35S 의 중심 자오선 (경도)를 찾아야 하는데, 동경 27도이다. 우리가 찾는 위치는 중심 자오선에서 서쪽으로 85,000m이다. 편북 값과 마찬가지로 편동(X) 값에도 음의 부호가 붙기 때문에 -85,000m가 되는데 여기에 UTM 정의에 따라 가짜 편동 값 500,000m를 더해야 한다. 즉 우리가 찾는 위치 좌표의 편동(X) 값은 415,000m(-85,000m + 500,000m)이다. 마지막으로 정확한 값을 얻으려면 이 편동 값에 구역 번호 를 붙여야 한다. 따라서 우리가 찾는, UTM 구역 35S로 투영된 관심 지역의 좌표는 35 415,000m E / 6,450,000m N이라고 표기될 것이다. 일부 GIS에서는 시스템 내에서 UTM 구역 35S을 정확하게 정의하고 단위를 미터로 설정한 경우, 이 좌표를 간단하게 415,000 6,450,000이라고 표시할 수도 있다.[3]
동영상[편집]
각주[편집]
참고자료[편집]
- 〈좌표계〉, 《네이버 국어사전》
- 〈좌표계〉, 《네이버 국어사전》
- 〈좌표계〉, 《위키백과》
- 〈좌표계〉, 《나무위키》
- 〈GIS에 대한 친절한 소개 » 8. 좌표계〉, QGIS Documentation
같이 보기[편집]

 위키원
위키원