구면좌표계
구면좌표계(球面座標係, spherical coordinate system)는 3차원 공간 상에 존재하는 점을 나타내는 좌표계 중 하나이다. 중심에서의 거리, 방위각, 위도를 이용하여 3차원 위치를 표시하는 방법이다.[1]
목차
개요[편집]
구면좌표계란 3차원 공간상에 존재하는 점을 나타내는 좌표계 중 하나로 보통 원점에서의 거리 r과 양의 방향의 z축과 이루는 각도θ, 그리고 z축을 축으로 하여 양의 방향의 x축과 이루는 각도로 표시한다. 우리가 살고 있는 은하 내에는 천억 개 이상의 별들이 있다. 그러나 그중에서 맨눈으로 볼 수 있는 별은 6000개 정도밖에 되지 않지만, 이들을 연구하기 위해 어디에서 얼마만큼 위치에 있는지를 결정해야 한다. 한 예로 지구상의 위치를 표시할 때 경도와 위도로써 정확히 표현할 수 있다. 마찬가지로 별들도 그것을 결정하는 방법들이 여러 가지 있는데 그중 한 가지가 바로 구면좌표계를 이용하는 것이다.[2]
특징[편집]
구면좌표계는 3차원 공간 상의 점들을 나타내는 좌표계의 하나로, 보통 (r, Φ, θ)로 나타낸다. 원점에서의 거리 r은 0부터 ∞까지, 양의 방향의 z축과 이루는 각도 θ는 0부터 π까지, z축을 축으로 양의 방향의 x축과 이루는 각 Φ는 0부터 2π까지의 값을 갖는다. θ는 위도로, Φ는 경도로 표현되는 경우도 있기도 한다.
이 세 수치를 보고, 다음과 같은 방법으로 공간의 점을 찾을 수 있다.: 원점 (0, 0, 0)에서 r만큼 z축을 따라 간다. 그 지점에서 x z 평면 안에 있으면서 z축에서부터 θ만큼 회전한다. 이 xz 평면 전체를 z축을 축으로 Φ만큼 반 시계방향(+x축에서 +y축 방향으로)으로 돌린다.
구면좌표계라는 이름은 이 좌표계에서 'r = 1'이 단위구(單位球)를 표현하기 때문에 붙여졌다. 또한 이 좌표계가 구대칭을 기치로 하기 때문이기도 하다.
구면좌표계와 원통좌표계는 평면 극좌표계를 공간으로 확장한 것이며, 구면좌표계는 구대칭이 나타나는 문제에서 유용하게 쓰인다. 예를 들어, 수소원자와 같이 구대칭이 있는 경우에 슈뢰딩거 방정식을 풀 때 구면좌표계를 사용한다.
아래 변환식을 통해 직교좌표계와 변환할 수 있지만, 변환식에서 사용하는 역삼각함수는 일의적이지 않기 때문에, 공간상의 각 점마다 하나의 좌표만 대응하는 직교좌표계와는 달리, 구면좌표계는 한 점을 나타내는 표현이 여러 가지일 수 있다. 예를 들어, (1, 0°, 0°), (1, 0°, 45°), 과 (-1, 180°, 270°)는 모두 같은 점을 나타낼 수 있다.[3]
표시 문자[편집]
세 좌표의 표시를 위한 여러 가지 다른 약속이 존재한다. 국제 표준 기구의 지침(ISO 31-11)에 따라 물리학에서는 (r, θ, φ)의 문자를 사용하여 원점에서의 거리, 천정과 이루는 각도(천정거리), 방위각 등을 표시하고, (미국의) 수학에서는 고도와 방위각이 바뀌어 'φ'와 'θ'로 표시된다.[3]
정의[편집]
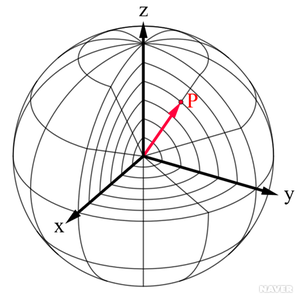
좌표 (r, Φ, θ)는 다음과 같이 정의 된다. 주어진 점을 P라 한다. r : 원점으로부터 P까지의 거리. θ : z축의 양의 방향으로부터 원점과 P가 이루는 직선까지의 각 Φ : x축의 양의 방향으로부터 원점과 P가 이루는 직선을 xy평면에 투영시킨 직선까지의 각.
구면좌표계의 경우는 좌표값에 따라 한 점을 여러 좌표가 가리키는 경우가 있으므로, 각 변수의 범위를 보통 아래와 같이 제한한다.
- r ≥ 0
- 0 ≤ θ ≤ π
- 0 ≤ Φ < 2π[3]
좌표 변환[편집]
다른 3차원 좌표계로 변환하는 공식은 다음과 같다.
직교좌표계
- 직교좌표계에서 구면좌표계로 변환시:
- 구면좌표계에서 직교좌표계로 변환시:
x =r sin θ cos Φ
y = r sin θ sin Φ
z = r cos θ
지리좌표계
δ = 90° - θ, or
θ = 90° - δ
원통좌표계
- 원통좌표계에서 구면좌표계로 변환시:
- 구면좌표계에서 원통좌표계로 변환시:
p = r sin θ
z = r cos θ[3]
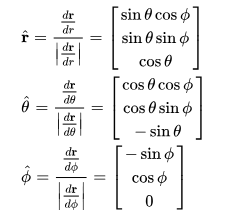
단위벡터[편집]
각 단위벡터의 직교좌표에서의 표현은 다음과 같다.[3]
종류[편집]
천구좌표계[편집]
천구좌표계는 천문학에서 위성, 행성, 항성, 은하 등 천체의 위치를 나타낼 때 사용하는 좌표계이다. 즉, 천체 관측에서 천체의 위치를 나타내기 위해 지구를 중심으로 나타낸 좌표계이다. 천구좌표계는 구면좌표계의 일종으로, 하늘을 둘러싼 가상의 구인 천구에서 천체의 방향을 가리키는 방식을 사용하는데, 이는 3차원으로 좌표를 표현하려면 해당 지점까지의 위치를 알아야 하는데, 천문학에서는 천체까지의 위치를 정확히 알 수 없거나, 거리가 중요하지 않은 경우도 많기 때문이다. 기본적으로 구면좌표계를 사용하며, 천구상의 위치만 필요하기에 거리는 표기하지 않는다. 따라서 두 각도 성분을 통해 천체의 위치를 표시하게 된다.
천구좌표계의 개념을 이해하기 위해 먼저 천구의 개념을 이해할 필요가 있는데, 천구는 실제로 존재하지 않는 가상의 구(球)로써 과거의 천문학에서 쓰였던 것을 현재까지 쓰고 있다. 관측자를 중심으로 거대한 반지름을 갖는 구를 설정하고, 모든 천체가 구의 표면에서 움직인다는 것을 전제로 하는 개념이다. 즉 천동설을 기반으로 나온 개념이다. 따라서 관측의 편리함 때문에 계속 사용하고 있을 뿐 과학적으로 큰 의미가 있는 것은 아니며, 우주에 대한 이해가 깊어진 현대 천문학에서는 천체 관측 이외에는 천구를 사용하지 않는다.
천구좌표(天球座標, Celestial Coordinates)는 천구 위에 천체의 위치를 나타낸 좌표를 말한다. 일반적으로 여러 종류의 경선(經線)과 위선(緯線)으로 이루어지는 구면 좌표가 사용되며, 은하좌표·적도좌표·지평좌표·황도좌표 따위가 있다. 천구상의 어느 지점의 위치를 표시하는 데 사용하는 좌표를 말한다. 지구상의 어느 지점을 위도와 경도로 표시하는 것과 같은 구면 좌표이다. 천체의 구면상의 좌표로 지평좌표, 적도좌표, 황도좌표가 주로 쓰인다. 천구(天球, celestial sphere)는 천체의 시위치(視位置)를 정하기 위하여 관측자를 중심으로 하는 무한 반경의 큰 구면(球面)을 말한다. 모든 천체가 실제 거리와는 관계없이 이 구면 위에 투영되어 있는 것으로 본다.[4][5][6][7]
우리가 사는 은하 내에는 천억 개 이상의 별들이 있다. 그중에서 맨눈으로 볼 수 있는 별은 6000개 정도밖에 되지 않지만, 이들을 연구하기 위해서는 각각의 별이 어디에 있는지를 결정할 필요가 있다. 별들의 위치를 결정하는 방법으로는 보통구면좌표계를 이용한다. 구면좌표계는 3차원 공간상에 존재하는 점을 나타내는 좌표계 중 하나로, 중심에서의 거리, 방위각, 위도를 이용하여 3차원 위치를 표시하는 방법이다. 천구 좌표계는 구면좌표계의 방법을 이용해 천구상의 위치를 나타내는 여러 좌표계를 뜻하며, 지평좌표와 적도좌표, 황도좌표, 은하좌표가 있다.[8]
적도좌표계[편집]
적도좌표계(赤道座標系, Equator Coordinates System)는 지구를 중심으로 한 가장 기본적인 좌표계로, 대부분의 천체는 이 적도 좌표계를 이용해 위치를 표시하고 관측을 하게 된다. 먼저 지구의 적도를 연장시킨 가상의 대원을 천구에 그린다. 이것을 천구의 적도라 부른다. 그리고 지구의 북극을 연장시켜 천구에 표시하고 이 점을 천구의 북극이라 부르고, 지구의 남극을 연장시켜 천구에 표시한 점을 천구의 남극이라 부른다. 그 다음으로 황도(黃道)와 천구의 적도가 만나는 두 점을 표시하고, 이 중 태양이 남반구에서 북반구로 이동할 때의 점을 춘분점, 다른 한 점을 추분점이라고 한다.
천구의 북극과 천구의 남극을 지나는 대원을 시간권(또는 시권, hour circle)이라고 부른다. 따라서 천구의 적도와 시간권은 수직이다. 춘분점을 지나는 시간권을 기준으로 관측하고자 하는 천체의 시간권까지의 각도를 반시계 방향으로 잰 각도를 적경(right ascension)이라고 하며 (그림상에서 α에 해당하는 각도), 0º~360º 또는 0시~24시로 표현한다. 즉, 춘분점이 기준이므로 춘분점에서의 시각이 0이며 반시계 방향으로 적경이 증가한다. 다음으로 관측하고자 하는 천체의 시간권을 따라 천구의 적도를 기준으로 잰 각도를 적위(declination)라 하며 (그림상에서 δ에 해당하는 각도) -90º~90º 의 값을 갖는다. 천구의 적도가 기준이므로 천구의 적도의 적위가 0º, 천구의 북극의 적위가 90º, 천구의 남극의 적위가 -90º 이다.
연주시차와 별의 고유 운동을 생각하지 않는다면, 태양계 천체 이외의 모든 별들은 천구상에서 운동하지 않는다. 즉 고유한 적경과 적위값을 가지므로, 찾고자 하는 천체의 적경과 적위값만 안다면 손쉽게 별들의 위치를 찾을 수 있다. 또 과거에 행성이 중요했던 이유는 이들이 다른 별들과 달리 움직였기 때문이다. 세차운동 때문에 춘분점과 천구의 적도의 위치는 조금씩 계속 변화하므로, 적도좌표계에 따른 좌표는 시간이 지나면 조금씩 달라진다. 그러므로 실제 천문학에서 적도좌표계를 사용할 때는 적도좌표계 결정의 기준이 되는 시점(역기점)을 정의해야 한다. 현대에는 2000년의 분점 위치를 기준으로 하는 J2000을 주로 사용하고 과거에는 각각 1900년과 1950년을 가준으로 하는 B1900과 B1950을 썼다. 따라서 과거의 학술 자료를 참조할 때는 천체의 좌표를 나타낼 때 B1900이나 B1950을 사용하였을 가능성이 높기 때문에 역기점을 반드시 확인해야 한다. 별자리 경계의 경우 1875년을 역기점으로 하는 적도좌표계에 근거해 경계를 정했기 때문에, J2000이나 현재 기준의 적도좌표계에서는 별자리 경계가 시간권과 조금씩 어긋난다.[5]
- 적경(a) : 춘분점을 따라 반시계 방향으로 천체의 시간권까지 잰 값(0~24h)
- 적위(δ) : 천구의 적도면에서 천체까지의 각을 시간권을 따라 남북 방향으로 잰 값(0~±90도)[8]
지평좌표계[편집]
지평좌표계(地平座標系, Horizontal Coordinate System)는 지구의 관측자를 중심으로 한 좌표계로, 일단 그냥 알기 쉬운 장점이 있다. 자신이 있는 점을 기준으로 다 해결하면 된다. 관측자를 중심으로 천구를 향해 선을 그어 만나는 점을 천정, 아래쪽으로 만나는 점을 천저, 그리고 관측자가 서있는 면을 확장시켜 천구와 만나게 되는 대원을 지평선이라 한다. 방위를 기준으로 지평선과 북쪽이 만나는 점을 북점, 남쪽과 만나는 점을 남점이라 한다. 주로 북점을 기준으로 하는 별까지의 각도를 방위각 (0º~360º), 지평선을 기준으로 하는 별까지의 높이 각도를 고도(0º~90º)라고 한다. 따라서 북점의 방위각은 0º, 남점은 180º 이고 천정의 고도는 90º 이다. 또한 관측자를 기준으로 하므로 지평면 아래의 보이지 않는 별들은 보통 신경쓰지 않는다.[5]
- 고도(h) : 천체를 지나는 수직권을 따라 지평면에서 천체까지 잰 각
- 방위각(A) : 천체를 지나는 수직권과 자오선 사이를 북점을 기준으로 시계방향으로 잰 각(0~360도)
- 천정 거리(z) : 천정에서 천체까지의 각도(z=90도-h)[8]
황도좌표계[편집]
황도좌표계는 황도면을 기준면으로, 춘분점 방향을 기준점으로 한 구면좌표계로서 지구나 태양이 좌표계의 중심에 있다. 즉, 지구의 공전궤도면을 기준으로 한 좌표계이다. 황경·황위의 두 가지 좌표로 나타내진다. 황도는 천구에서 태양이 다니는 길로 적도와 기울어져 있다. 태양계에 있는 천체의 위치를 표시할 때 편리하며, 천체의 위치는 황경과 황위로 나타낸다. 황경은 황도를 따라 춘분점에서 천체의 방향까지 잰 각으로 0도에서 360도 범위의 값을 가진다. 각을 재는 방향은 황도의 북극에서 보았을 때 반시계방향이다. 황위는 지구의 관측자가 볼 때 황도에 투영된 천체의 방향과 천체 사이의 각으로 –90도에서 +90도의 값을 가진다. 황도의 북극이 있는 쪽이 양의 값을 그 반대 방향이 음의 값을 갖는다.[9][10]
- 황경(λ) : 황도상에서 춘분점으로부터 동쪽으로 잰 각거리(0~360도)
- 황위(β) : 황도상에서 황도의 북극과 남극으로 잰 각거리[8]
은하좌표계[편집]
은하좌표계(銀河座標系)는 은하적도를 제일기준원으로 하며 은경과 은위의 두 요소로 목표 천체의 좌표를 표시하는 좌표계이다. 은하좌표계는 은하계 내의 항성의 위치와 분포를 조사하는 데 편리하므로 이 분야의 연구에 사용되며 은하 좌표계와 적도 좌표계의 관계를 나타내려면 은하 좌표계의 원점을 적도 좌표계로 나타내면 된다. 은하 좌표는 적도 좌표와 마찬가지로 은경(銀經)과 은위(銀緯)를 이용하여 위치를 나타낸다. 은경과 은위는 모두 도·분·초로 나타낸다. 은경은 은하 좌표의 경도(經度)로, 은하 중심 방향으로부터 은하 적도를 따라 동쪽으로 측정한 각거리이다. 춘분점을 기점으로 은하적도를 따라 동쪽으로 0도에서 360도까지 측정한다. 은위는 은하 좌표의 위도(緯度)로, 은하 적도에서 은하 북극과 은하 남극 쪽으로 측정한 거리이다. 은하 적도를 기준으로 북쪽에 위치한 천체에 대해서는 + 기호를, 남쪽에 위치한 천체에 대해서는 -기호를 붙이고, 0도에서 90도까지 측정한다.[11]
- 은경(l) : 은하 중심 방향으로부터 은하 적도를 따라 동쪽으로 잰 각(0~360도)
- 은위(b) : 은하 적도에서 은하 북극과 은하 남극 쪽으로 잰 각(0~±90도)[8]
동영상[편집]
각주[편집]
참고자료[편집]
- 〈일식〉, 《네이버 국어사전》
- 〈구면좌표계〉, 《천문학습관》
- 〈구면좌표계〉, 《물리학백과》
- 〈구면좌표계〉, 《수학백과》
- 〈구면좌표계〉, 《위키백과》
- 〈천구좌표계〉, 《위키백과》
- 〈천구좌표계〉, 《나무위키》
- 〈천구 좌표〉, 《국방과학기술용어사전》
- 〈천구좌표〉, 《천문학 작은사전》
- 〈천구좌표계〉, 《지구과학산책》
- 〈황도좌표계〉, 《천문학 작은사전》
- 〈황도좌표계〉, 《천문학백과》
- 〈은하좌표계〉, 《위키백과》
같이 보기[편집]

 위키원
위키원