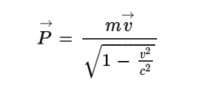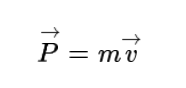고전역학
고전역학(古典力學, classical mechanics)은 뉴턴의 운동법칙을 기본으로 하는 역학이다. 고전역학은 질량이 일정한 입자의 어떤 시각에서의 위치와 속도를 정하면 그 앞뒤의 운동을 정할 수 있다고 보는 결정론적 해석이 바탕에 있다.
G.갈릴레이의 물체운동론(물체의 낙하법칙), J.케플러의 행성(行星)의 운동법칙(케플러의 제1, 제2, 제3 법칙) 등의 맥락을 이어 학문적으로 체계화된 뉴턴역학을 기초로 하고 있다. 그 근본적인 원리는 뉴턴의 운동법칙이다. 입자의 질량은 일정하므로 어떤 시각의 위치와 속도를 정하면 입자의 운동을 완전히 결정할 수 있다는 법칙으로 거의 모든 거시적인 역학현상을 설명할 수 있었다. 다른 한 편으로는 양자역학과 대비되는 말로서 상대성이론까지 포함하기도 하지만 대부분의 경우 뉴턴역학만을 가리킨다.
고전역학은 물리학 중 가장 오래된 분야이며, 뉴턴 이후 급속히 발전하여 오일러, J.L.라그랑주, 해밀턴을 거쳐 19세기 말 완성되었다. 특히 J.L.라그랑주, P.S.라플라스 등에 의해 해석적으로도 발전하였는데, 그 근본적인 입장은 뉴턴의 입장과 같다. 여기에 반하여 상대성이론의 경우 질량은 일정하다고 보지 않으며, 운동에 대한 견해도 근본적으로 다르다. 한편 양자역학에 의하면 운동은 확률론적으로밖에 정해지지 않으며, 고전역학과 같은 인과율(因果律)에 입각한 결정론적 견해를 부정하고 있다. 고전역학은 20세기로 접어들면서 약간의 수정이 있었을 뿐 더 이상 발전하지 않고 있으며, 앞으로 발전할 가능성이 별로 없는 것으로 알려져 있다.
개요[편집]
고전 역학은 극단적으로 무겁거나 속력이 빛의 속력에 근접하는 경우가 아닌 거시적인 물체들에 대한 운동 법칙을 기술한다. 현실 세계의 물체를 점입자로 간략화 함으로써 운동 법칙을 기술하는 뉴턴 역학(Newtonian mechanics)과 더불어, 위치와 운동량을 동시에 기술하는 위상 공간을 통해 운동하는 입자들을 기술하는 라그랑주 역학(Lagrangian mechanics)과 해밀턴 역학(Hamiltonian mechanics)의 방법론을 포함하고 있다. 즉, 고전 역학은 주로 20세기에 개발된 상대론(Relativistic mechanics)과 양자 역학(Quantum mechanics)을 제외한 그 이전의 역학체계를 의미한다.
고전 역학적인 방법론은 기술하고자 하는 물체의 현재 상태를 알고 있으면 미래에 어떻게 움직일 것인지 알 수 있으며 또한 이것이 과거에는 어떻게 움직여왔는지 알 수 있다는 생각을 기반에 두고 있다. 뉴턴 역학에서 점입자에 위치, 질량, 인가된 힘을 결정하여 해당 시스템의 특징을 정의하였고, 이 방법이 라그랑주 역학과 해밀턴 역학에서 해당 입자의 위치와 운동량을 동시에 기술하는 위상공간에서의 해석까지 발전하였다. 이들은 에너지를 최소화 하는 과정으로 물질계가 변화한다는 법칙 그리고 최소작용의 원리를 이용함으로써 새로운 물리학 해석의 관점을 제공해주었다.
고전 역학의 발전 이후에 개발된 이론들이 그림 2에 정리되어 있다. 속력이 빛의 속력에 근접하는 경우를 다루는 특수 상대론(special relativity)과 빠른 속력 혹은 공간의 휘어짐을 통해 극단적으로 무거워지는 경우를 다루는 일반 상대론(general relativity)이 있으며 미시적인 물체들에 대한 운동을 기술하는 양자 역학(quantum mechanics), 그리고 수많은 자유도(degree of freedom)를 가지는 양자적인 수준의 물체에 대해서 기술하는 양자장론(quantum field theory)이 있다. 하지만 일반 상대론과 양자장론을 결합하여 극도로 작고 무거워서 밀도가 극도로 높은 경우에 사용할 수 있는 양자중력이론(quantum gravity)은 아직 존재하지 않는다. 위와 같은 이론들은 20세기 이후에 개발되었으며 물리학에 대한 새로운 패러다임의 전환을 가져다주었으므로 위 이론들의 개발 시기와 사용된 방법론을 기점으로 고전 역학을 분류한다.
고전 역학의 한계는 이후 개발된 이론들과 비교해보면 명확히 알 수 있다. 상대론적인 입장에서, 고전 역학은 절대적인 시간 축을 정의하고 3차원의 공간의 좌표를 변환하는 갈리레이변환(Galilean transformation)을 사용하는 반면, 현대 이론은 상대적인 시간 축의 개념을 도입해 공간과 함께 4차원 시공간에서 좌표를 변환하는 로렌츠변환(Lorentz transformation)을 사용하고 있다. 이는 공간과 시간을 엮어주는 속력을 기준으로 질량, 에너지, 길이 등이 변화할 수 있음을 의미하며 빛의 속력은 등속도, 가속도 등을 경험하고 있는 어떤 좌표계에서도 일정하다는 사실을 절대적인 기준으로 채택하고 있다. 한편 양자 역학의 입장에서는, 입자의 위치와 운동량을 동시에 정확히 기술하는 것을 위상공간에 적용하는 것이 틀렸음을 지적해주고 있다. 이는 어떤 입자의 위치와 운동량이 위치 좌표계와 운동량 좌표계에서 동시에 각각 하나의 점으로 표시될 수 없다는 의미이다. 양자 역학에서는 불확정성의 원리(uncertainty principle)를 통해 어떤 입자의 위치가 위치 좌표계에서 특정 값을 가지고 있음을 의미하는 점으로 표시되었다면 운동량 좌표계에서는 똑같은 확률로 입자가 모든 운동량을 가질 수 있음을 말해주고 있으며, 어떤 입자의 운동량이 운동량 좌표계에서 특점 값을 가지고 있음을 의미하는 점으로 표시되었다면 위치 좌표계에서는 똑같은 확률로 모든 좌표 지점에 입자가 존재함을 말해주고 있다. 보통의 경우는 좁은 위치에 입자가 발견될 확률이 쏠려 있고 이로부터 입자의 크기가 정의되고 그 입자의 운동량에 대한 불확정성도 적당한 범위를 가지고 존재한다.
고전 역학 이후에 개발된 이론들은 고전 역학의 범주를 아우르고 있다. 다음의 두 사례를 통해서 상대성 이론과 양자 역학이 고전 역학으로 회귀할 수 있다.
상대성 이론[편집]
상대성 이론에서 어떤 입자의 운동량은 다음과 같이 주어진다.
여기서 m은 질량, v→는 속도, v는 속력, c는 빛의 속력이다.
만약에, v가 c에 비하여 매우 작다면, v²/c²≈ 0 이 되므로, 느린 속력을 가진 물체에 대해서 운동량은 다음과 같이 주어지게 된다.
이는 뉴턴 역학에서 운동량에 해당하므로 상대성 이론은 고전 역학을 포함하고 있다.
양자역학[편집]
고전 역학에서 사용하고 있는 입자성의 근사는 어떤 입자가 스스로 가지고 있는 고유의 드 브로이 파장(de Broglie wavelength)보다 작은 시스템에 속할 때 성립하지 않게 된다. 상대론적인 효과를 받고 있지 않는 느린 속력을 가진 입자에 대해서 드 브로이 파장은 다음과 같이 주어진다.
λ = h/p
여기서 h 는 플랑크 상수, p는 해당 입자의 운동량이다.
예를 들어, 전자와 같이 질량이 작은 입자가 좁은 공간에 있는 CPU내부 도선의 경우(오른쪽 그림), 전자의 드 브로이 파장이 도선의 폭보다 길어서 스스로에 의한 간섭으로 인해 양자 역학적인 효과가 발생하므로 설계에 이를 반영해야 한다. 하지만, 넓은 공간에서 날아다니는 전자는 입자와 같이 직진성이 강해진다. 대표적인 예시로 핵분열 과정에서 발생하는 베타선(빠르게 날아가는 전자)이 피해를 주는 경우에 해당한다. 따라서 어떤 입자가 자신의 드 브로이 파장보다 좁은 공간에 있으면 고전 역학으로 설명할 수 없는 현상을 나타냄과 동시에 더 넓은 공간에 있으면 고전 역학에서의 예측처럼 행동할 수 있으므로 양자 역학은 고전 역학을 포함하고 있다.
참고자료[편집]
같이 보기[편집]

 위키원
위키원