인장응력
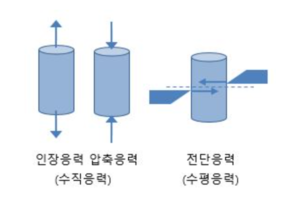
인장응력(引張應力 , tensile stress)은 인장력에 의해 생기는 응력이다. 압축 주응력에 직각 방향으로 인장응력이 생긴다. 재료가 외력을 받아 축 방향으로 작용하는 하중에 대하여 그 반대쪽으로 반발하는 힘, 즉, 재료 내부에서 일어나는 응력은 인장응력이다.
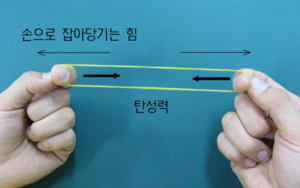
인장응력은 쉽게 생각해서 고무줄을 생각하면 된다. 고무줄을 처음에 당겼을 때는 별로 힘이 들지 않고 당겨지지만, 어느 정도 이상 당겼을 때는 힘이 많이 들게 된다. 그리고 너무 많이 잡아당기면 가운데가 조금씩 찢어지다가 '팅'하면서 끊어진다. 인장응력은 이처럼 재료를 잡아당겼을 때 생기는 저항력을 의미한다.
개요[편집]
수직응력은 어떤 재료의 중심축에 수직방향으로 작용하는 힘에 의한 응력을 말한다. 방향에 따라 압축응력과 인장응력이 있다. 재료 표면의 법선 방향으로 작용하므로 법선응력(Normal Stress)이라고도 한다.
길이가 L인 기다란 막대가 있다고 하자. 이 막대의 한 쪽 끝을 벽에 단단히 고정하고 다른 쪽 끝을 잡은 뒤 막대 방향으로 크기 F만큼의 인장력을 가하면 이 막대는 강체가 아닌 이상 길이가 늘어나는 변형이 일어난다. 이때 막대가 늘어난 길이를 x라고 하자. 이때 주어진 재료 막대의 변형율(Strain)은 ε=x/L이다. 이때 막대의 변형은 응력(Stress)에 의해 일어난 것이다.
응력은 막대의 단면에 작용하는 단위면적당 힘이므로, 막대의 단면의 면적을 A라고 했을 때 막대에 가해지는 응력은 σ=F/A이다. 훅의 법칙(Hooke’s Law)은 막대에 가하는 힘과 변형된 길이는 탄성 한계 내에서 비례한다는 것이므로 막대를 잡아당기는 힘 F와 막대가 늘어난 길이 x사이에는 F=kx의 관계가 성립한다. 여기서, k는 비례상수이다. 이 식의 양변을 막대의 길이 L과 막대의 단면적 A로 나누면, F/LA=kx/LA.
이 식을 정리하여 변형율과 응력에 대한 식으로 바꾸면 σ=kL/A=Eε이다. 여기서 응력과 변형율이 탄성 한계 내에서 비례관계이므로 비례상수 kL/A는 비례상수 E로 쓴다. E는 '탄성 계수'(modulus of elasticity)다. 탄성계수 E는 물질의 고유한 성질이며, 여기에 재료의 단면적을 곱하고 재료의 길이로 나누면 그 재료의 스프링 상수를 알 수 있다. 이를 '영률' 혹은 '영의 계수'(Young’s modulus)라고 한다.
이때 변형율 ε의 값이 양수(+)일 경우 인장이라고 하며, 이때 작용하는 응력 σ를 인장 응력(Tensile Stress)이라고 한다. 변형율의 값이 음수(-)일 경우에는 압축이라고 하며, 작용하는 응력을 압축응력(Compressive Stress)이라고 한다.
부호는 인장응력을 +, 압축응력을 -로 표시한다.
인장응력에 의한 변화[편집]
어떤 재료에 인장응력이 가해진다고 생각해 보겠다. 막대를 양쪽에서 잡아당기면 용수철처럼 힘에 비례해서 길이가 늘어난다. 여기서 늘어난 길이를 변형이라고 하며, 변형을 원래 길이로 나눈 상대적인 값을 변형률(strain)이라 한다. 예를 들어, 10cm였던 고무줄을 잡아 당겨서 15cm가 됐다면 늘어난 5cm만큼을 원래의 길이인 10cm로 나누는 계산법이며, 이 인장응력에 따른 변형률은 5/10=0.5가 되는 것이다.
응력과 관련한 유명한 법칙 중 하나인 후크의 법칙(Hook's law)에 따르면 탄성범위 내에서 '응력(σ)과 변형률(ε)은 비례한다'고 설명한다. 즉 σ=Еε라는 수식으로 표현할 수 있다. 이 수식 중에 E는 비례상수로, 물질의 탄성계수라 한다. 탄성계수가 큰 재료는 잘 늘어나지 않는 딱딱한 특성이 있는 것으로 생각하면 된다.
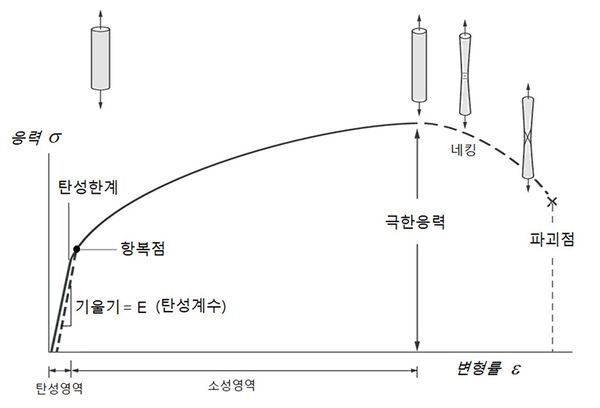
만약 재료를 세게 잡아당겨 응력이 탄성범위를 넘어서면, 재료는 원래의 상태로 돌아오지 못하게 된다. 고무줄을 적당히 잡아당겼다 놓으면 원래 모습으로 돌아가지만, 너무 세게 잡아당기면 끊어져 버리듯이, 고체가 외부에서 탄성 한계 이상의 힘을 받아 형태가 바뀐 뒤, 가해지던 힘이 없어져도 더 이상 본래의 모양으로 돌아가지 않는 성질을 소성(塑性, plasticity)이라고 한다. 응력이 항복점(降伏點, 탄성과 소성의 경계점)까지 넘어서면 재료는 엿가락처럼 늘어나게 되는데 이것을 '소성변화'라고 한다. 여기서 더욱 세게 잡아당기면 재료는 늘어지며 목이 가늘어지는 네킹(necking) 현상이 발생하고 결국은 끊어지게 된다. 따라서 구조물을 설계할 때 재료에 주어지는 응력이 항복점을 넘지 않도록 유의해야 한다.
인장응력 공식[편집]
σ(응력도) = P(power)/A(area: 단면적) 이기 때문에 P= σ × A로 계산할 수 있다.
인장응력의 단위[편집]
보통 국제표준 단위계인 SI unit에서는 PA(N/㎡), MPA(N/㎟), GPA(KN/㎟) 을 많이 쓰고, 미국 관용 단위계에서는 psi(lb/in²), ksi(kips/in² )을 많이 쓴다. (참고) 이 두 단위계의 단위를 혼용해서 쓰면 안된다.
압축응력 및 인장응력[편집]
압축 스트레스 인장 응력 결과 재료 압착의 압축 응력 결과. 재료 스트레칭의 인장 응력 결과 밀기 또는 당기기 압축응력은 외력에 의해 몸의 모양과 크기를 변경하는 힘이다. 인장응력은 모양과 크기를 변경하기 위해 외부 힘에 의해 신체에 가해지는 힘이다. 압축 또는 신장 외부 압축력에 의해 압축응력이 생성된다. 신장력이 늘어나려고 하기 때문에 인장응력이 발생한다. 바에 적용 바가 압축 응력을 받으면 변형은 압축된다 (음수). 바가 인장 응력을 받으면 변형은 인장 (양수)이다.
참고자료[편집]
- 〈인장응력〉, 《자동차용어사전》
- 〈인장응력〉, 《용어해설》
- 라그나로크, 〈(Stress 1장) σ: 수직응력(Normal Stress): 축 응력(Axial stress) 알아보기 (인장응력/압축응력)〉, 《네이버 블로그》, 2018-07-15
- 〈압축 응력: 5가지 중요한 사실〉, Lambda Geeks
- Avraham Kim, 〈(Basic Engineering) 2. 응력이란? 〉, 《네이버 블로그》, 2017-01-04
- 스터디캐드캠, 〈재료 > 금속 > 응력(stress)〉, 《네이버 블로그》, 2016-02-11
- 스터디캐드캠, 〈인장응력〉, 《티스토리》, 2021-01-22
같이 보기[편집]

 위키원
위키원