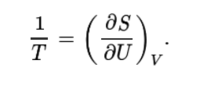절대온도
절대온도(absolute temperature)는 열역학의 표준온도로 켈빈온도(Kelvin temperature)라고도 한다. 단위는 K(케이)이다. 절대영도를 온도의 기준점인 0K로 하고, 섭씨온도와 같은 온도 눈금으로 잰 온도가 절대온도이다. 즉, 두 온도의 차이가 절대온도로 1 K라면, 섭씨온도로도 1 °C이다. 절대영도는 자연에서 존재할 수 있는 가장 낮은 온도이다. 절대온도 T와 섭씨온도 c 의 관계는 T = c + 273.15로 주어진다. 즉, 절대영도는 -273.15 °C이다.
목차
개요[편집]
절대온도는 물질의 특이성에 의존하지 않는 절대적인 온도를 가리킨다. 1848년 켈빈(W.톰슨)이 도입하였다. 통계역학적으로 엔트로피를 알면 절대온도 T를 구할 수 있다. 열역학 제2 법칙에 따라 정해진 온도로, 열역학적으로 분자운동이 정지한 상태인 이론상 생각할 수 있는 최저온도를 기준으로 한 온도를 말한다. 국제도량형위원회는 모든 온도 측정의 기준으로 절대온도를 채택하고 있다.
- K의 정의
기존의 정의는 물의 삼중점의 열역학적 온도의 1/273.16이었으나 2018년 제26차 CGPM(국제도량형위원회)에서 재정의된 켈빈은 볼츠만 상수 k를 J K⁻¹ 단위로 나타낼 때 1.380649×10⁻²³이 되도록 정의된다. 여기서 J K⁻¹은 kg m² s⁻² K⁻¹과 같은 단위이다.
샤를의 법칙과 절대온도[편집]
여러 종류의 기체를 이용한 실험에서, 일정한 압력에서 온도를 점점 낮추면 기체의 부피가 점점 줄어드는 것을 볼 수 있다. 이를 샤를의 법칙이라고 한다. 실제의 기체는 온도를 낮춰가면 액화가 일어나서 기체상태에서 액체상태로의 상전이가 일어나지만, 분자 사이의 상호작용을 무시하는 이상기체를 상정하면, 이상기체의 부피가 결국 0으로 수렴하는 특정한 온도가 이론적으로 존재할 것으로 추측할 수 있다. 바로 이 온도가 절대영도이다. 절대영도를 최저 온도의 기준점으로 하고, 섭씨온도와 같은 온도눈금으로 정의한 온도가 바로 절대온도다.
기체분자운동론과 절대온도[편집]
계를 구성하는 분자의 운동에너지의 평균값은 온도가 올라가면 증가한다. 거꾸로 온도를 점점 내리면, 고전역학적인 분자들의 운동에너지는 결국 0이 될 것을 예상할 수 있다. 이 온도가 바로 절대영도이다. 운동에너지는 속도의 제곱에 비례하므로, 항상 0보다 크거나 같은 값만을 가질 수 있으므로, 절대영도에 해당하는 온도에서 출발해서 온도를 더 낮추는 것은 불가능하다.
양자역학적인 계와 절대온도[편집]
양자역학을 따르는 계는 온도가 점점 내려가면 더 낮은 에너지 상태에 도달하게 된다. 만약 계가 가질 수 있는 에너지의 바닥상태가 오로지 하나로 유일하다면, 온도가 내려갈 때 결국 계는 이 에너지 바닥상태에 놓이게 되는데, 이 온도가 바로 절대영도이다. 양자역학을 통해서 잘 이해할 수 있는 흑체복사 현상에서는 흑체가 발산하는 에너지의 총량이 흑체의 온도의 네제곱에 비례한다는 스테판-볼츠만 법칙이 잘 알려져 있다. 이 법칙의 온도 단위도 절대온도이다.
열역학제일법칙과 절대온도[편집]
열역학제일법칙은 계의 내부에너지 U 의 변화량 dU 가 계에 유입된 열에너지와 일의 양과 같아야 한다는 에너지보존법칙이다. 가역적인 준정적과정을 상정하면 내부에너지의 변화량(dU)을 엔트로피의 변화량(dS)과 부피의 변화량(dV)을 이용해 아래와 같이 쓸 수 있다.
dU = TdS - pdV
여기서 T는 절대온도, p는 압력이다. 위의 식을 이용해 절대온도를 아래와 같이 정의할 수 있다.
따라서, 절대온도 T 가 0보다 낮을 수 없다는 것은, 부피 V가 일정할 때 엔트로피 S가 계의 에너지의 증가함수라는 것과 관계가 있다는 것을 알 수 있다. 또, 볼츠만의 엔트로피 공식 S(E) = KB log W(E) 로 부터, 계의 에너지가 E일 때, 계가 가질 수 있는 미시적인 상태의 수 W 는 E 의 증가함수라는 것도 알 수 있다. 만약, 높은 에너지에서 더 많은 미시적인 상태가 존재한다면, 절대온도 T 는 0보다 크거나 같아야 한다.
음의 절대온도[편집]
위의 논의로부터, 만약 특정한 조건에서 엔트로피가 에너지의 감소함수가 될 수 있다면, 음의 절대온도가 가능하다는 것을 생각할 수 있다. 엔트로피가 에너지의 함수로 감소하다가 극소점을 지나 다시 증가하는 경우, 계의 에너지가 엔트로피의 극소점에 미치지 못할 때는 음의 절대온도를, 극소점을 지나서는 양의 절대온도를 갖게 된다. 즉, 음의 절대온도에 도달하기 위해서는 양의 값을 갖는 절대온도가 양의 무한대에 먼저 도달(1/T →0+)해야 하고 이를 넘어 1/T →0- 가 가능해지면 음의 절대온도가 구현된다. 이로부터, '음의 절대온도는 양의 절대온도보다도 더 뜨겁다'는 설명을 이해할 수 있다. 즉, 현실에서 양의 절대온도를 가지는 계에서 출발해서 온도를 낮추어 음의 절대온도에 도달하는 것은 불가능하지만, 적절히 구현한 실험상황에서 계를 음의 절대온도의 상태에 놓게 되면, 계는 계속 음의 절대온도를 가지게 된다. 에너지의 함수로서의 엔트로피의 극대값이 어떤 에너지값에서 존재해서, 그보다 더 높은 에너지에서는 엔트로피가 줄어드는 다양한 이론적인 모형계가 있다. 상호작용하지 않는 이준위계 (non-interacting two-level system)가 대표적인 예이다.
과학에서의 사용[편집]
온도의 표준 단위이므로 온도 값을 요구하는 대부분의 계산에서는 켈빈온도를 쓴다. 섭씨온도에 273.15를 더하면 켈빈온도가 된다. 물리나 화학에서 유독 27℃가 많이 보이는 이유는 상온 상태를 가정할 수 있으면서도 절대온도로 300 K가 되어 계산이 편해지기 때문이다.
고전역학의 이론적 배경에서는 0 K은 가진 에너지가 전혀 없는 상태를 뜻하기 때문에 0 K 아래 온도는 있을 수 없다는 것이 맞았지만, 양자역학이 발달한 이후 0 K 상태에서도 에너지가 존재함이 알려졌는데, 바닥 상태의 이런 에너지를 영점에너지(zero point energy)라고 한다. 위치에너지가 0이라고 할지라도 불확정성 원리에 따라 운동에너지를 0에 맞출 수 없고, 이에 따라 조화 진동자는 (1/2)hf만큼 에너지가 있다.
빛이 거의 닿지 않는 오지에 위치한 행성의 최저 온도도 12 K] 아래가 드물고, 심지어 항성의 빛이 미치지 못하는 공간의 온도조차 3 K. 즉 영하 270도 정도고 심지어 부메랑 성운과 같이 항성이 죽어가면서 사실상 빛이 닿지 않는 데다 바람까지 세게 부는, 그야말로 온도 내려갈 조건이 갖춰질 대로 갖춰진 지역조차도 1 K가 한계다. 당연히 태양계같이 항성의 열이 미치는 곳의 온도는 더 높다.
다만 준위의 수가 실질적으로 유한하게 된 계(예: 극저온으로 냉각된 고체 LiF 속의 F핵)에서는 열역학 3법칙을 우회하여 절대영도 이하로 온도(T<0)가 내려갈 수 있다. 보통 시스템은 에너지/열을 받을수록 엔트로피가 올라가므로 마이너스 켈빈이 될 수 없지만 특수한 시스템에선 최대한 받을 수 있는 열 또는 열용량의 한계가 있고, 이 이상으로 에너지/열을 받으면 엔트로피가 오히려 내려간다. 이후 무조건적으로 에너지를 주는 상태가 된다. 이 시스템의 현재 열용량은 마이너스가 되므로, 온도는 무한을 넘어 마이너스가 된다는 개념이다. 절대영도 항목에도 나온다. 2013년 1월 3일 네이처지에 양자 가스를 이용해 절대영도보다 낮은 온도를 만들었다는 연구가 실렸다(Quantum gas goes below absolute zero). 단 여기에 따르면 이 현상을 음의 온도라는 말로 표현하는 것일 뿐, 이는 여전히 절대영도보다는 따뜻한 온도이며 우리가 아는 절대 온도의 법칙이 깨진 것은 아니라고. 보통은 입자들이 낮은 에너지 준위를 선호하는데 이 경우는 반대로 에너지 분포가 높기 때문에 음의 온도라고 '부를 수 있다.'는 것이라고 한다.
참고자료[편집]
같이 보기[편집]

 위키원
위키원