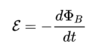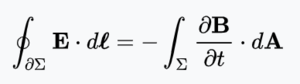"패러데이 법칙"의 두 판 사이의 차이
잔글 |
잔글 |
||
| 12번째 줄: | 12번째 줄: | ||
== 전자기 유도 법칙 == | == 전자기 유도 법칙 == | ||
| − | '''패러데이 전자기 유도 법칙'''(Faraday, Faraday's law of electromagnetic induction)은 자기 선속의 변화가 기전력을 발생시킨다는 법칙이다. 1831년 영국의 물리학자 마이클 패러데이가 발견하였다. [[맥스웰 방정식]] 중 하나이며, 패러데이 법칙에서 자기선속의 양자화가 유도되기도 한다. 전자기유도에 의해 회로 내에 유발되는 [[기전력]]의 크기는, 회로를 관통하는 자기력선속(磁氣力線束)의 시간적 변화율에 비례한다. 기전력의 방향을 정하는 렌츠의 | + | '''패러데이 전자기 유도 법칙'''(Faraday, Faraday's law of electromagnetic induction)은 자기 선속의 변화가 기전력을 발생시킨다는 법칙이다. 1831년 영국의 물리학자 마이클 패러데이가 발견하였다. [[맥스웰 방정식]] 중 하나이며, 패러데이 법칙에서 자기선속의 양자화가 유도되기도 한다. 전자기유도에 의해 회로 내에 유발되는 [[기전력]]의 크기는, 회로를 관통하는 자기력선속(磁氣力線束)의 시간적 변화율에 비례한다. 기전력의 방향을 정하는 [[렌츠의 법칙]]과 함께 전자기유도가 일어나는 방식을 나타낸다. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
;패러데이 법칙 | ;패러데이 법칙 | ||
| 36번째 줄: | 29번째 줄: | ||
맥스웰-패러데이 방정식은 네 가지 맥스웰 방정식의 한가지로 고전 전자기학에서 기초적인 역할을 한다. 적분의 형태로 표현하면 켈빈-스토크스의 정리에 의하여 | 맥스웰-패러데이 방정식은 네 가지 맥스웰 방정식의 한가지로 고전 전자기학에서 기초적인 역할을 한다. 적분의 형태로 표현하면 켈빈-스토크스의 정리에 의하여 | ||
| − | + | [[파일:맥스웰-패러데이 방정식.png|썸네일|300픽셀|가운데|]] | |
식의 좌변이 말하는 것은 폐곡선 에서 극소길이 '''''dl'''''에 따라 전기장을 적분하면 우변에서와 같이 자기장을 시간에 따라 편미분한 값을 면적 '''''dA'''''에 대해 적분한 값의 음수값을 취한다. | 식의 좌변이 말하는 것은 폐곡선 에서 극소길이 '''''dl'''''에 따라 전기장을 적분하면 우변에서와 같이 자기장을 시간에 따라 편미분한 값을 면적 '''''dA'''''에 대해 적분한 값의 음수값을 취한다. | ||
| + | |||
| + | ;역사 | ||
| + | 전자기유도현상은 마이클 패러데이와 요셉 헨리가 1831년 독자적으로 발견하였지만, 패러데이가 그의 연구 결과로서 처음으로 출판하였다. 1831년 8월 29일 전자기 유도에 대한 패러데이의 첫 번째 실험적 증명에서 철제 고리(또는 토러스)를 두 개의 와이어로 반대 방향에 감았다. 발견된 전자석의 특성에 대한 그의 평에 근거하여 하나의 와이어에 전류가 흐를 때, 파동의 부분이 고리를 따라 반대편에 전달되어 약간의 전기적 효과를 일으킬 것이라 생각했다. 하나의 와이어를 검류계에 연결하고 다른 한 쪽을 배터리에 연결하였을 때 일어나는 변화를 관찰하였다. 패러데이는 와이어를 배터리에 연결할 때 와 떼어낼 때 과도전류(패러데이는 이것을 '전기 파동'이라 불렀다.)를 관측했다. 이 유도현상은 배터리가 연결되었다 분리될 때 발생하는 자기력선속의 변화 때문에 발생한 것이다. 두 달 후, 패러데이는 몇 가지 다른 전자기유도의 단서들을 찾았다. 예를 들면, 막대자석을 코일에 빠르게 통과시킬때 과도전류가 발생하는 것을 보았고 막대 자석 근처에서 회전하는 동판에 의해 교류가 발생하는 것이 있다. (패러데이의 디스크) | ||
| + | |||
| + | 패러데이는 전자기 유도 현상을 그가 역선라고 부른 개념을 가지고 설명했다. 그러나 당시 과학자들은 그의 이론적 아이디어가 수학적으로 공식화되지 못했다며 이를 부정했다. 한 명의 예외가 있었다면 그것은 맥스웰이었다. 그는 패러데이의 생각을 자신의 양적 전자기학 이론의 근간으로 삼았다. 맥스웰의 논문에서, 전자기유도에 대한 관점을 다양하게 한 시기는 올리버 헤비사이드가 패러데이 법칙이라고 언급한 미분 방정식으로서 표현된다.(사실 이것은 패러데이 법칙의 원형 형식과 약간 다르고 운동 기전력을 설명하지 않는다) 헤비사이드가 수정한 것이 오늘날 맥스웰 방정식으로 알려진 방정식에서 패러데이 법칙을 나타낸다. | ||
| + | |||
| + | 1834년에 하인리히 렌츠가 만든 렌츠의 법칙은 회로를 통과하는 전기력선속을 설명하고 유도기전력과 전자기유도현상으로 인한 전류의 방향을 제시한다. | ||
== 참고자료 == | == 참고자료 == | ||
2021년 9월 13일 (월) 14:40 판
패러데이 법칙(Faraday's law )은 영국 국민으로부터 가장 존경받는 물리학자 마이클 패러데이에 의해 1833년 발견한 전기분해 법칙과 1831년에 발견한 전자기유도 법칙이 이에 해당한다. 오늘날 다양한 곳에서 쓰이는 생활 속에서 없어서는 안 될 위대한 원리다. 전기분해 법칙에 의해 물질의 원자 구조와 관련해서 전기량에도 최소 단위(기본 전하량)가 존재한다는 것이 처음으로 예측되었고, 전자기유도 법칙은 전자기유도가 일어나는 방식을 밝혀냈다.
전기분해 법칙
전기분해를 하는 동안 전극에 흐르는 전하량(전류×시간)과 전기분해로 인해 생긴 화학변화의 양 사이의 정량적인 관계를 나타내는 법칙이다. 1833년 패러데이가 논문을 발표하였으며, 전기화학의 가장 기본적인 법칙이다.
- 제1법칙 : 전해질용액을 전기분해할 때 전극에서 석출되는 물질의 질량은 그 전극을 통과한 전자의 몰수에 비례한다. 즉, 전류가 더 많이 흐를수록 시간이 지날수록 석출되는 물질의 질량은 많아진다.
- 제2법칙 : 같은 전기량에 의해 석출되는 물질의 질량은 물질의 종류에 관계없이 각 물질의 화학 당량에 비례한다. 즉, 1그램당 량의 물질량을 전기분해하여 석출하는 데 필요한 전기량은 물질의 종류에 관계없이 96,485.3383C으로 항상 일정하다.
제1법칙에 의해 석출되는 물질의 양은 전류와 시간의 곱에 비례한다. 그리고 공급되는 전자가 전해질 속의 이온을 원자가 되게 하여 석출되므로, 석출되는 물질의 질량은 원자량에 비례한다. 또한 원자가가 곧 이온 한 개가 원자로 될 때 필요한 전자개수이므로, 석출되는 물질의 질량은 원자가에 반비례한다.
물질 1그램당 량을 전기분해로 얻는데 필요한 전하량, 곧 전자 1몰의 전하량을 패러데이 상수라고 한다. 보통 기호 F로 표시하며, F = 96,485.3383C/mol e⁻이다. 이 법칙에 의해 물질의 원자구조와 관련해서 전기량에도 최소 단위(기본 전하량)가 존재한다는 것이 처음으로 예측되었다. 즉, 1F은 전자의 기본전하량(1.602×10⁻¹⁹C/e⁻)과 아보가드로수(6.02×10²³ mol⁻¹)의 곱과 같다. 전하량 1C으로 석출되는 물질의 양은 은 1.118mg, 수소기체 0.010446mg이다. 1C의 전기량에 의해 석출되는 물질의 양을 그 물질의 전기화학당량이라 한다.
전자기 유도 법칙
패러데이 전자기 유도 법칙(Faraday, Faraday's law of electromagnetic induction)은 자기 선속의 변화가 기전력을 발생시킨다는 법칙이다. 1831년 영국의 물리학자 마이클 패러데이가 발견하였다. 맥스웰 방정식 중 하나이며, 패러데이 법칙에서 자기선속의 양자화가 유도되기도 한다. 전자기유도에 의해 회로 내에 유발되는 기전력의 크기는, 회로를 관통하는 자기력선속(磁氣力線束)의 시간적 변화율에 비례한다. 기전력의 방향을 정하는 렌츠의 법칙과 함께 전자기유도가 일어나는 방식을 나타낸다.
- 패러데이 법칙
물리학에서 전기장과 자기장의 상호간 유도현상을 설명하는 것이 패러데이 법칙으로, 임의의 폐회로에서 발생하는 유도 기전력의 크기는 폐회로를 통과하는 자기선속의 변화율과 같다는 것을 의미한다. 수학식으로는 다음과 같이 표현할 수 있다.
ΦB : 자기 선속, ℰ : 기전력
여기서 우변에 '−'가 붙은 이유는 렌츠의 법칙에 따라 전기 회로에서 발생하는 유도 기전력은 폐회로를 통과하는 자속의 변화를 방해하는 방향으로 발생하기 때문이다.
맥스웰-패러데이 방정식
맥스웰-패러데이 방정식은 네 가지 맥스웰 방정식의 한가지로 고전 전자기학에서 기초적인 역할을 한다. 적분의 형태로 표현하면 켈빈-스토크스의 정리에 의하여
식의 좌변이 말하는 것은 폐곡선 에서 극소길이 dl에 따라 전기장을 적분하면 우변에서와 같이 자기장을 시간에 따라 편미분한 값을 면적 dA에 대해 적분한 값의 음수값을 취한다.
- 역사
전자기유도현상은 마이클 패러데이와 요셉 헨리가 1831년 독자적으로 발견하였지만, 패러데이가 그의 연구 결과로서 처음으로 출판하였다. 1831년 8월 29일 전자기 유도에 대한 패러데이의 첫 번째 실험적 증명에서 철제 고리(또는 토러스)를 두 개의 와이어로 반대 방향에 감았다. 발견된 전자석의 특성에 대한 그의 평에 근거하여 하나의 와이어에 전류가 흐를 때, 파동의 부분이 고리를 따라 반대편에 전달되어 약간의 전기적 효과를 일으킬 것이라 생각했다. 하나의 와이어를 검류계에 연결하고 다른 한 쪽을 배터리에 연결하였을 때 일어나는 변화를 관찰하였다. 패러데이는 와이어를 배터리에 연결할 때 와 떼어낼 때 과도전류(패러데이는 이것을 '전기 파동'이라 불렀다.)를 관측했다. 이 유도현상은 배터리가 연결되었다 분리될 때 발생하는 자기력선속의 변화 때문에 발생한 것이다. 두 달 후, 패러데이는 몇 가지 다른 전자기유도의 단서들을 찾았다. 예를 들면, 막대자석을 코일에 빠르게 통과시킬때 과도전류가 발생하는 것을 보았고 막대 자석 근처에서 회전하는 동판에 의해 교류가 발생하는 것이 있다. (패러데이의 디스크)
패러데이는 전자기 유도 현상을 그가 역선라고 부른 개념을 가지고 설명했다. 그러나 당시 과학자들은 그의 이론적 아이디어가 수학적으로 공식화되지 못했다며 이를 부정했다. 한 명의 예외가 있었다면 그것은 맥스웰이었다. 그는 패러데이의 생각을 자신의 양적 전자기학 이론의 근간으로 삼았다. 맥스웰의 논문에서, 전자기유도에 대한 관점을 다양하게 한 시기는 올리버 헤비사이드가 패러데이 법칙이라고 언급한 미분 방정식으로서 표현된다.(사실 이것은 패러데이 법칙의 원형 형식과 약간 다르고 운동 기전력을 설명하지 않는다) 헤비사이드가 수정한 것이 오늘날 맥스웰 방정식으로 알려진 방정식에서 패러데이 법칙을 나타낸다.
1834년에 하인리히 렌츠가 만든 렌츠의 법칙은 회로를 통과하는 전기력선속을 설명하고 유도기전력과 전자기유도현상으로 인한 전류의 방향을 제시한다.

 위키원
위키원