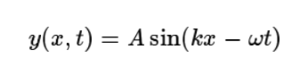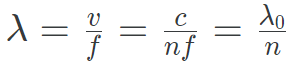파장

파장

파장(波長, wavelength)은 공간에 퍼져 있는 파동의 한 번의 주기가 가지는 길이이다. 결너비라고도 한다. 단위는 길이의 단위로, SI단위는 미터이다. 수식에 사용할 때에는 보통 λ(람다; lambda)로 표현한다.

파동의 진행 속도가 일정하다고 가정할 때, 진동수와 반비례 관계를 가진다. 따라서 소리의 파장이 짧을수록 높은 소리가 나고 파장이 길수록 낮은 소리가 난다.

파동과 헷갈리는 사람들이 있는데, 파동은 매질을 통해 진동이 퍼져나가는 현상 자체를 말하고, 파장은 이 진동이 퍼져나간 거리(길이)를 의미한다. 한자에서도 알 수 있듯이 파동은 '움직일 동(動)', 파장은 '길 장(長)'을 사용한다.

상세

파동에서 주어진 시각에 같은 모양이 반복되는 최소 길이를 파장이라 한다.

한편, 시간적으로 이에 대응되는 개념으로, 같은 장소에서 같은 모양이 반복되는 최소 시간을 주기(period)라고 한다.

파장은 일반적으로 사인파(sinusoidal wave)에서 많이 다루어진다. 사인파는

로 표현할 수 있는데, 여기서 y(x,t) 는 위치 x, 시각 t에서 파동이 가지는 변위(displacement)를 나타낸다. A 는 파동의 진폭(amplitude)이며, k 는 파수(wave number), ⍵ 는 각진동수(angular frequency)이다. 그러므로 파장은

λ = 2π/k

로 표현된다.

파장이 길면 파동이 장애물을 만나 작은 틈 사이로 지나갈 때 장애물 뒤로 휘어지는 회절(diffraction)이 크게 일어난다. 예를 들어 전파 중에서 AM 라디오 방송에서 사용하는 중파는 수백 미터에 이르는 파장을 가지므로 건물이나 언덕 사이를 휘어 돌아가며 전파되어 난청 지역이 거의 없다. 그러나 FM 라디오 방송이나 공중파 TV 방송에서 사용하는 초단파는 수 미터 정도의 파장을 가지고 있어 상대적으로 직진성이 강하므로 빌딩과 같은 장애물 뒤는 전파가 전달되지 못하는 난청 지역이 된다. 군사적으로는 산악 지역에서도 통신이 가능하기 위해 수십 미터에 이르는 라디오파를 사용한다. 그 결과 통신병이나 군용 자동차는 수 미터에 이르는 안테나가 장착된 무전기를 갖고 다닌다. (같은 원리에 의하면 AM 방송을 수신하기 위해서는 길이가 수백 미터에 이르는 비현실적인 안테나가 필요하여, 다른 원리를 이용하여 안테나를 제작한다.)

또한 파장은 반사되어 나오는 파동을 통해 물체를 구별할 때, 구별할 수 있는 최소 크기를 결정짓는다. 우리 눈에 보이는 가시광선의 파장은 400-700 nm이므로, 가시광선을 사용해서는 아무리 현미경의 배율을 높인다고 해도 1 nm보다도 작은 원자를 볼 수 없다. 그러나 파장이 1 nm 이하인 X선을 사용하면 원자를 구별해 낼 수 있다. 또한 파장이 최소 수 미터에 이르는 라디오파로는 비행기나 배를 구별해 내기 어렵다. 그러므로 제2차 세계대전 중에 파장이 수 cm인 전자기파를 발생시키는 기술이 개발되었고, 그런 전자기파가 반사되어 돌아오는 것을 통해 물체를 파악해 내는 기술이 개발되었는데, 이것이 레이다이다. 음파의 경우에는 수 mm 정도의 파장을 갖는 음파를 사용하여 태아의 모습을 구별해 내기도 하는데, 그러기 위해서는 인간이 들을 수 있는 진동수의 범위보다 훨씬 높은 진동수를 갖는 초음파를 사용해야 한다.

사인파가 아닌 주기적 파동

주기를 가지는 파동은 사인함수 모양이 아니더라도 파장을 정의할 수 있다. 사인파와 마찬가지로 y(x, t)=y(x+λ,t)를 만족하는 가장 작은 양수 λ를 파장이라 한다.

2차원 이상의 파동

평면이나 공간상에서는 파동의 위상이 일정한 지점들이 있다. 이렇게 위상이 일정한 점들이 이루는 선 또는 면을 파면이라 하는데, 파면을 기준으로 파장을 이야기할 수 있다. 물론 파면 사이의 거리가 일정하지 않는다면 파장의 의미가 모호해진다.

평면파

평면파는 파면이 평면을 이루며, 진행속도가 일정할 때 마루나 골 사이의 간격이 일정하다. 파장은 이 일정한 파면 사이의 거리로 정의한다.

평면파가 사인파일 때 아래와 같이 식으로 써진다.

원형파, 구면파

파면이 원 또는 구 모양을 이루며 퍼지는 파동을 가리키며, 각 파면은 동심원 형태를 이룬다.

다만 이 경우 파동을 매개로 에너지가 점에서 발산해서 일반적으로 진폭이 위치마다 다르기에, 단순히 변위의 크기가 극대인 큰 지점으로 이야기하지 않는다. 가령 진폭이 거리에 반비례하는 구면파는 아래와 같이 식이 써진다.

즉 파장의 기준이 되는 지점들은 위 사인함수의 값이 1인 지점을 가리키며, 변위의 크기가 극대인 지점들은 빨간색 항이 곱해져 있어서 다른 데 있다.

파수와 파장의 관계

진동수는 파동의 속력에서 파장으로 나눈 값으로, 파장이 같더라도 파동의 속력에 따라 달라질 수 있다. 한편 파동의 속력에 관계없이 파장과 반비례 관계를 가지는 물리량으로 파수가 있다.

파수는 단위 길이당 파장의 수를 나타내며, 파장의 역수이다.[2]

ν= λ⁻¹ = k/ 2π ​ 앞서 정의에서 k라고 써진 값은 단위 길이당 위상차로, 이 값을 파수로 이야기하기도 한다.

정상파

끈이나 관과 같이 길이가 제한된 매질에서 정상파가 형성되기 위한 조건은 파장에 달려 있다. 정상파의 파장은 마디와 마디 사이(혹은 배와 배 사이)의 간격의 두 배이다.

빛(전자기파)의 파장

빛은 어느 관성계에서 측정해도 동일한 속력을 가지므로, 진동수와 파장의 변환이 비교적 자유롭다. 빛의 속력이 동일하므로 진동수와 파장은 반비례 관계이다.

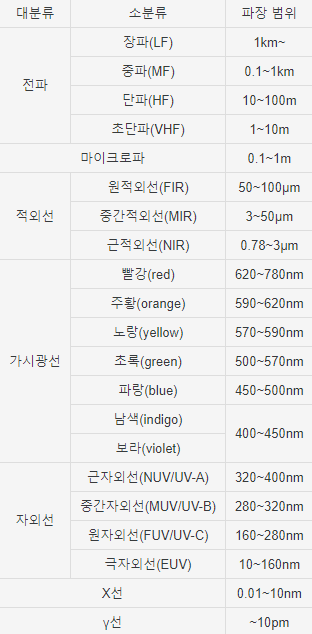
종류별 빛의 파장

진공에서 빛의 속력은 언제나 일정하므로 300,000km/s에서 아래 값들로 나누면 종류별 진동수가 나온다.

굴절률과 파장의 관계

빛이 물질을 지나갈 때 빛의 진행 속력이 느려진다. 그렇지만 빛의 진동수는 변하지 않기에 파장은 굴절률에 반비례함을 알 수 있다. 이를 수식으로 나타내면 아래와 같이 쓸 수 있다. λ₀,λ는 각각 진공 중의 파장과 물질 속의 파장이다.

가령 파장이 600nm인 빨간색 레이저 빛으로 이중슬릿 간섭무늬 실험을 굴절률이 1.33(대략 3분의 4)인 물에 담그고 할 때, 파장은 450nm로 줄며 간섭무늬의 간격도 4분의 3으로 줄어든다. 다만 물 속에서 파장이 450nm로 준다 해도 진동수는 변하지 않으므로 실험자는 여전히 빨간색 간섭무늬를 보게 된다.

참고자료

• 〈파장〉, 《물리학백과》
• 〈파장〉, 《위키백과》
• 〈파장〉, 《나무위키》

같이 보기

• 파동
• 파수
• 진동수

이 파장 문서는 에너지에 관한 글로서 검토가 필요합니다. 위키 문서는 누구든지 자유롭게 편집할 수 있습니다. [편집]을 눌러 문서 내용을 검토·수정해 주세요.

산업 : 산업, 산업혁명, 기술, 제조, 기계, 전자제품, 정보통신, 반도체, 화학, 바이오, 건설, 유통, 서비스, 에너지 □■⊕, 전기, 소재, 원소, 환경, 직업, 화폐, 금융, 금융사, 부동산, 부동산 거래, 부동산 정책, 아파트, 건물, 토지 에너지 SMR • 가속운동 • 가시광선 • 가열 • 각속도 • 감마선 • 감속운동 • 강력 • 고압 • 고온 • 고전역학 • 관성력 • 관성모멘트 • 광선 • 광속 • 광전자 • 광전효과 • 광합성 • 기압 • 냉각 • 냉방 • 뉴턴 • 대류 • 대체에너지 • 동력 • 동력원 • 라디오파 • 마이크로파 • 마찰 • 마찰계수 • 마찰력 • 마찰에너지 • 만유인력 • 만유인력의 법칙 • 무중력 • 물리에너지 • 바이오에너지 • 발열 • 발열반응 • 발화 • 방사선 • 방열 • 베타선 • 복사 • 복사선 • 복사에너지 • 부력 • 불 • 블루에너지 • 빛 • 빛에너지 • 삼투압 • 생물에너지 • 석유에너지 • 석탄에너지 • 섭씨 • 소리에너지 • 소수력 • 속력 • 수력 • 수력에너지 • 수소에너지 • 수압 • 수열 • 수열에너지 • 수직항력 • 신생에너지 • 신에너지 • 신재생 • 신재생에너지 • 알짜힘(합력) • 알파선 • 압력 • 압축응력 • 약력 • 양극선 • 양자역학 • 에너지 • 에너지밀도 • 에너지보존법칙 • 에너지원 • 에너지 효율 • 엑스선 • 엔트로피 • 역반응 • 역파장 • 역학적 에너지(기계에너지) • 열 • 열대류 • 열량 • 열복사 • 열분해 • 열에너지 • 열역학 • 열전도 • 열전도도 • 열전도율 • 열절연 • 열팽창 • 열팽창계수 • 열효율 • 온도 • 온도차 • 왕복에너지 • 왕복운동 • 운동에너지 • 원운동 • 원자력 • 원자력에너지 • 위치에너지 • 음극선 • 응력 • 인공태양 • 인장응력 • 인화 • 입자선 • 자외선 • 자유낙하 • 작용 • 재가열 • 재생에너지 • 저온 • 저압 • 적외선 • 전기에너지 • 전도 • 전자기력 • 절대온도 • 정반응 • 정지에너지 • 조력 • 조력에너지 • 조류에너지 • 줄 • 줄의 법칙 • 중력 • 중력에너지 • 지열 • 지열에너지 • 직사광선 • 직선운동 • 진동 • 진동에너지 • 진자 • 진자운동 • 천연에너지 • 청정에너지 • 친환경에너지 • 칼로리 • 탄성 • 탄성에너지 • 태양 • 태양광 • 태양광에너지 • 태양에너지 • 태양열 • 태양열에너지 • 텐서 • 파동 • 파력 • 파력에너지 • 파워 • 파장 • 폐기물에너지 • 폭발 • 풍력 • 풍력에너지 • 풍압 • 항력(드래그포스) • 해양에너지 • 핵반응 • 핵분열 • 핵분열에너지 • 핵붕괴 • 핵에너지 • 핵융합 • 핵융합에너지 • 화력 • 화씨 • 화학 • 화학에너지 • 회전 • 회전수 • 회전에너지 • 회전운동 • 흡열 • 흡열반응 • 힘 발전 교류발전기 • 마이크로 수력발전 • 물레방아 • 박테리아 발전소 • 발전 • 발전기 • 발전소 • 발전효율 • 변전소 • 비상발전기 • 소수력발전 • 소수력발전소 • 소형모듈원전(SMR) • 수력발전 • 수력발전소 • 원자력발전 • 원자력발전소 • 조력발전 • 조력발전소 • 조류발전 • 조류발전소 • 지열난방 • 지열발전 • 지열발전소 • 직류발전기 • 태양광발전 • 태양광발전소 • 태양광패널 • 태양열발전 • 태양열발전소 • 파력발전 • 파력발전소 • 풍력발전 • 풍력발전소 • 풍차 • 해양 온도차 발전 • 핵융합발전 • 핵융합발전소 • 화력발전 • 화력발전소 • 회전축 연료 CNG • LNG • LPG • 가스 • 가스충전소 • 가연성 • 갈탄 • 개질수소 • 경유(디젤) • 경질유 • 고급휘발유 • 고압가스 • 고체연료 • 그레이수소 • 그린수소 • 기체연료 • 나무 • 난방연료 • 두바이유 • 등유 • 땔감 • 면세유 • 무연탄 • 무연휘발유 • 바이오 • 바이오가스 • 바이오디젤 • 바이오매스 • 바이오에탄올 • 바이오연료 • 방사성물질 • 배기가스 • 배출가스 • 번개탄 • 부생수소 • 분별증류 • 뷰테인(부탄) • 브라운수소 • 브렌트유 • 블루수소 • 석유 • 석유화학 • 석탄 • 셰일가스 • 셰일오일 • 수소 • 수소연료 • 수소전기 • 순도 • 숯(목탄) • 압축가스 • 액체연료 • 액화가스 • 역청탄 • 연료 • 연료첨가제 • 연료화 • 연비 • 연소 • 연탄 • 오일샌드 • 오일셰일 • 옥탄가 • 용해가스 • 원유 • 유사경유 • 유연탄 • 유연휘발유 • 윤활유 • 일반휘발유 • 장작 • 점화 • 정유 • 정제 • 조개탄 • 주입 • 중유 • 중질유(中質油) • 중질유(重質油) • 증류 • 질소산화물 • 천연가스 • 천연자원 • 친환경연료 • 코크스 • 타르 • 텍사스유 • 프로페인(프로판) • 합성경유 • 핵연료 • 혼유 • 혼합가스 • 혼합기체 • 혼합연료 • 화석연료 • 화재 • 휘발유(가솔린) 위키 : 자동차, 교통, 지역, 지도, 산업, 기업, 단체, 업무, 생활, 쇼핑, 블록체인, 암호화폐, 인공지능, 개발, 인물, 행사, 일반