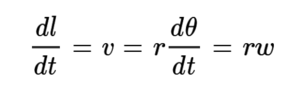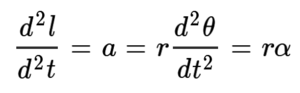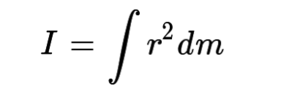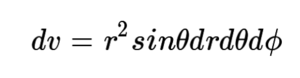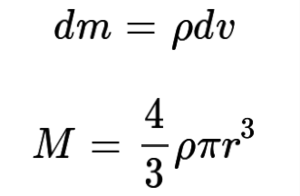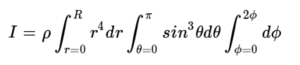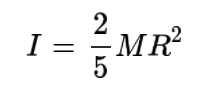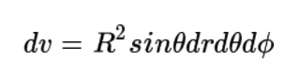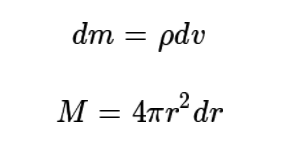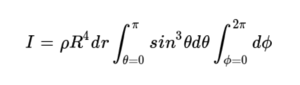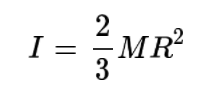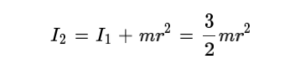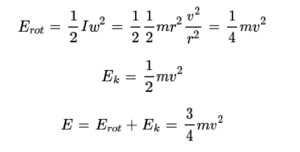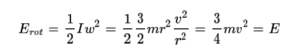"회전에너지"의 두 판 사이의 차이
잔글 |
|||
| 3번째 줄: | 3번째 줄: | ||
== 상세 == | == 상세 == | ||
회전운동의 본질은 [[원운동]]이며, 원운동은 아주 짧은 변위에서 [[선운동]]으로 근사될 수 있다. 기본적으로 원의 중심각과 반지름 그리고 호의 길이의 관계로부터 각속도를 정의할 수 있고, 각가속도와 돌림힘의 정의 또한 가능하다. | 회전운동의 본질은 [[원운동]]이며, 원운동은 아주 짧은 변위에서 [[선운동]]으로 근사될 수 있다. 기본적으로 원의 중심각과 반지름 그리고 호의 길이의 관계로부터 각속도를 정의할 수 있고, 각가속도와 돌림힘의 정의 또한 가능하다. | ||
| + | |||
'''''ㅣ = rθ''''' | '''''ㅣ = rθ''''' | ||
| 13번째 줄: | 14번째 줄: | ||
다음으로 질량은 관성 모멘트(moment of inertia), 힘은 돌림힘(torque), 운동량은 각운동량(angular momentum)에 대응됨을 보자. 각운동에서의 변수들과 물리량의 관계는 선운동과 놀랍도록 닮아 있다. 변위, 속도, 가속도는 각변위, 각속도, 각가속도와 연결되며, 질량과 관성 모멘트의 연결은 다음과 같은 관계로 이루어진다. | 다음으로 질량은 관성 모멘트(moment of inertia), 힘은 돌림힘(torque), 운동량은 각운동량(angular momentum)에 대응됨을 보자. 각운동에서의 변수들과 물리량의 관계는 선운동과 놀랍도록 닮아 있다. 변위, 속도, 가속도는 각변위, 각속도, 각가속도와 연결되며, 질량과 관성 모멘트의 연결은 다음과 같은 관계로 이루어진다. | ||
[[파일:회전에너지 식3.png|썸네일|300픽셀|가운데|]] | [[파일:회전에너지 식3.png|썸네일|300픽셀|가운데|]] | ||
| − | 관성 모멘트는 부피가 있는 강체를 수많은 미소 부피 요소로 나눈 뒤, 회전의 중심으로부터 부피 요소까지의 거리의 제곱()과 부피 요소의 질량()을 곱하여 더한다. 따라서 질량이 같은 강체끼리도 기하학적 요인에 의해 관성 모멘트가 달라질 수 있음에 유의하여야 한다. | + | 관성 모멘트는 부피가 있는 강체를 수많은 미소 부피 요소로 나눈 뒤, 회전의 중심으로부터 부피 요소까지의 거리의 제곱(''r²'')과 부피 요소의 질량(''dm'')을 곱하여 더한다. 따라서 질량이 같은 강체끼리도 기하학적 요인에 의해 관성 모멘트가 달라질 수 있음에 유의하여야 한다. |
예를 들어, 질량이 M으로 같지만 속이 찬 반지름이 R인 구와 속이 빈 구 껍질의 관성 모멘트를 비교해보자. 이때 회전축은 구의 중심을 통과하고 밀도는 균일하다고 가정한다. 구좌표계에서 미소 부피는 다음과 같이 표현된다. | 예를 들어, 질량이 M으로 같지만 속이 찬 반지름이 R인 구와 속이 빈 구 껍질의 관성 모멘트를 비교해보자. 이때 회전축은 구의 중심을 통과하고 밀도는 균일하다고 가정한다. 구좌표계에서 미소 부피는 다음과 같이 표현된다. | ||
[[파일:회전에너지 식4.png|썸네일|300픽셀|가운데|]] | [[파일:회전에너지 식4.png|썸네일|300픽셀|가운데|]] | ||
| − | 속이 찬 구의 밀도를 라 하면, | + | 속이 찬 구의 밀도를 '''''ρ''''' 라 하면, |
[[파일:회전에너지 식5.png|썸네일|300픽셀|가운데|]] | [[파일:회전에너지 식5.png|썸네일|300픽셀|가운데|]] | ||
| − | 미소 부피는 회전축으로부터 만큼 떨어져 있으므로 관성 모멘트는 다음과 같은 적분으로 구할 수 있다. | + | 미소 부피는 회전축으로부터 '''''rsinθ''''' 만큼 떨어져 있으므로 관성 모멘트는 다음과 같은 적분으로 구할 수 있다. |
[[파일:회전에너지 식6.png|썸네일|300픽셀|가운데|]] | [[파일:회전에너지 식6.png|썸네일|300픽셀|가운데|]] | ||
이를 계산하면 다음과 같다. | 이를 계산하면 다음과 같다. | ||
[[파일:회전에너지 식7.png|썸네일|300픽셀|가운데|]] | [[파일:회전에너지 식7.png|썸네일|300픽셀|가운데|]] | ||
| − | 반면, 속이 빈 구 껍질의 경우 미소 부피는 회전축으로부터 만큼 떨어져 있으며 미소 부피는 다음과 같이 표현된다. | + | 반면, 속이 빈 구 껍질의 경우 미소 부피는 회전축으로부터 '''''Rsinθ''''' 만큼 떨어져 있으며 미소 부피는 다음과 같이 표현된다. |
[[파일:회전에너지 식8.png|썸네일|300픽셀|가운데|]] | [[파일:회전에너지 식8.png|썸네일|300픽셀|가운데|]] | ||
| − | 구 껍질의 밀도를 라 하면 | + | 구 껍질의 밀도를 '''''ρ''''' 라 하면 |
[[파일:회전에너지 식9.png|썸네일|300픽셀|가운데|]] | [[파일:회전에너지 식9.png|썸네일|300픽셀|가운데|]] | ||
미소 부피는 회전축으로부터 만큼 떨어져 있으므로 관성 모멘트는 다음과 같은 적분으로 구할 수 있다. | 미소 부피는 회전축으로부터 만큼 떨어져 있으므로 관성 모멘트는 다음과 같은 적분으로 구할 수 있다. | ||
| 35번째 줄: | 36번째 줄: | ||
[[파일:여러 모양의 물체의 관성 모멘트 (출처 - 한국물리학회).jpg|썸네일|800픽셀|가운데|그림 1. 여러 모양의 물체의 관성 모멘트 (출처 - 한국물리학회)]] | [[파일:여러 모양의 물체의 관성 모멘트 (출처 - 한국물리학회).jpg|썸네일|800픽셀|가운데|그림 1. 여러 모양의 물체의 관성 모멘트 (출처 - 한국물리학회)]] | ||
[[파일:빗면을 굴러 내려가는 원기둥 모양의 강체.png|썸네일|400픽셀|그림 2. 빗면을 굴러 내려가는 원기둥 모양의 강체]] | [[파일:빗면을 굴러 내려가는 원기둥 모양의 강체.png|썸네일|400픽셀|그림 2. 빗면을 굴러 내려가는 원기둥 모양의 강체]] | ||
| − | 빗면을 따라 굴러 내려가는 원기둥 모양의 강체를 그린 그림이다. 속이 꽉 찬 원기둥의 관성 모멘트는 이고, 여기서 은 원기둥의 질량, 은 원기둥 밑면의 반지름이다. 회전하며 내려가는 원기둥의 운동을 분석할 때, 회전의 중심을 원기둥 밑면의 중심을 지나며 옆면에 평행한 축으로 할 때와 원기둥과 빗면이 접촉하는 선을 축으로 할 때, 평행축 정리에 따라 원기둥의 관성 모멘트가 달라진다. 회전축 1에 의한 관성 모멘트 과 회전축 2에 의한 관성 모멘트 의 관계는 평행축 정리에 의해 다음과 같다. | + | 그림 2는 빗면을 따라 굴러 내려가는 원기둥 모양의 강체를 그린 그림이다. 속이 꽉 찬 원기둥의 관성 모멘트는 '''''½mr²''''' 이고, 여기서 '''''m''''' 은 원기둥의 질량, '''''r''''' 은 원기둥 밑면의 반지름이다. 회전하며 내려가는 원기둥의 운동을 분석할 때, 회전의 중심을 원기둥 밑면의 중심을 지나며 옆면에 평행한 축으로 할 때와 원기둥과 빗면이 접촉하는 선을 축으로 할 때, 평행축 정리에 따라 원기둥의 관성 모멘트가 달라진다. 회전축 1에 의한 관성 모멘트 '''''I₁''''' 과 회전축 2에 의한 관성 모멘트 '''''I₂''''' 의 관계는 평행축 정리에 의해 다음과 같다. |
[[파일:회전에너지 식12.png|썸네일|300픽셀|가운데|]] | [[파일:회전에너지 식12.png|썸네일|300픽셀|가운데|]] | ||
| − | 이제 원기둥의 질량중심을 회전축으로 정할 때와 원기둥과 빗면과의 접촉면을 회전축으로 정할 때 회전 에너지는 다르지만 총 운동 에너지는 여전히 같음을 보이자. 먼저, 물체는 빗면에서 마끄러지 않고, 물체의 질량중심이 속력 로 운동한다고 가정한다. 이때 선속도와 각속도의 관계에 의해 다음이 성립한다. | + | 이제 원기둥의 질량중심을 회전축으로 정할 때와 원기둥과 빗면과의 접촉면을 회전축으로 정할 때 회전 에너지는 다르지만 총 운동 에너지는 여전히 같음을 보이자. 먼저, 물체는 빗면에서 마끄러지 않고, 물체의 질량중심이 속력 ''''' v''''' 로 운동한다고 가정한다. 이때 선속도와 각속도의 관계에 의해 다음이 성립한다. |
'''v = r ⍵''' '''⍵ = v/r''' | '''v = r ⍵''' '''⍵ = v/r''' | ||
회전축 1을 기준으로 삼을 때는 회전 운동과 질량중심의 선운동이 동시에 존재하며, 각각의 에너지는 다음과 같다. | 회전축 1을 기준으로 삼을 때는 회전 운동과 질량중심의 선운동이 동시에 존재하며, 각각의 에너지는 다음과 같다. | ||
| + | [[파일:회전에너지 식13.png|썸네일|300픽셀|가운데|]] | ||
| + | 이는 질량중심이 속도 ''v→ '' 로 움직일 때 선운동에 의한 운동 에너지뿐만 아니라 회전운동에 의한 회전 에너지가 존재함을 명백히 보여준다. 이어서 회전축 2를 기준으로 삼을 때는 질량중심의 선운동 효과가 평행축 정리에 의해 관성 모멘트에 더해지므로 운동 에너지의 총량은 오로지 회전 에너지에 의존한다. | ||
[[파일:회전에너지 식14.png|썸네일|300픽셀|가운데|]] | [[파일:회전에너지 식14.png|썸네일|300픽셀|가운데|]] | ||
따라서 어떤 회전축을 설정하는지에 관계없이 물체의 에너지가 일정하다는 것을 알 수 있다. | 따라서 어떤 회전축을 설정하는지에 관계없이 물체의 에너지가 일정하다는 것을 알 수 있다. | ||
2021년 11월 18일 (목) 11:28 판
회전에너지(rotational energy)는 회전하고 있는 물체 또는 입자가 지니는 에너지를 의미한다. 회전운동의 운동에너지라고 볼 수 있다. 회전운동을 할 때 회전에너지는 물체가 회전운동을 유지하려는 정도를 나타내는 물리량인 관성 모멘트에 비례하며, 일정 시간동안 움직인 각을 나타내는 각속도의 제곱에 비례한다. 식은 다음과 같다. E = ½I⍵² .( I =관성 모멘트, ⍵ =각속도) 회전에너지 또한 동일하게 다른 에너지로 변환 가능하며, 에너지 보존법칙에 따라 전체 에너지는 보존된다. 풍력발전이 바로 이 바람을 통해 회전에너지를 생성하고 이를 전기에너지로 바꾸는 것이다.
상세
회전운동의 본질은 원운동이며, 원운동은 아주 짧은 변위에서 선운동으로 근사될 수 있다. 기본적으로 원의 중심각과 반지름 그리고 호의 길이의 관계로부터 각속도를 정의할 수 있고, 각가속도와 돌림힘의 정의 또한 가능하다.
ㅣ = rθ
양변을 시간에 대해 미분하면
이것이 선속도와 각속도 사이의 관계다. 이를 한 번 더 미분하면
이것이 가속도와 각가속도 사이의 관계다.
다음으로 질량은 관성 모멘트(moment of inertia), 힘은 돌림힘(torque), 운동량은 각운동량(angular momentum)에 대응됨을 보자. 각운동에서의 변수들과 물리량의 관계는 선운동과 놀랍도록 닮아 있다. 변위, 속도, 가속도는 각변위, 각속도, 각가속도와 연결되며, 질량과 관성 모멘트의 연결은 다음과 같은 관계로 이루어진다.
관성 모멘트는 부피가 있는 강체를 수많은 미소 부피 요소로 나눈 뒤, 회전의 중심으로부터 부피 요소까지의 거리의 제곱(r²)과 부피 요소의 질량(dm)을 곱하여 더한다. 따라서 질량이 같은 강체끼리도 기하학적 요인에 의해 관성 모멘트가 달라질 수 있음에 유의하여야 한다.
예를 들어, 질량이 M으로 같지만 속이 찬 반지름이 R인 구와 속이 빈 구 껍질의 관성 모멘트를 비교해보자. 이때 회전축은 구의 중심을 통과하고 밀도는 균일하다고 가정한다. 구좌표계에서 미소 부피는 다음과 같이 표현된다.
속이 찬 구의 밀도를 ρ 라 하면,
미소 부피는 회전축으로부터 rsinθ 만큼 떨어져 있으므로 관성 모멘트는 다음과 같은 적분으로 구할 수 있다.
이를 계산하면 다음과 같다.
반면, 속이 빈 구 껍질의 경우 미소 부피는 회전축으로부터 Rsinθ 만큼 떨어져 있으며 미소 부피는 다음과 같이 표현된다.
구 껍질의 밀도를 ρ 라 하면
미소 부피는 회전축으로부터 만큼 떨어져 있으므로 관성 모멘트는 다음과 같은 적분으로 구할 수 있다.
이를 계산하면 다음과 같다.
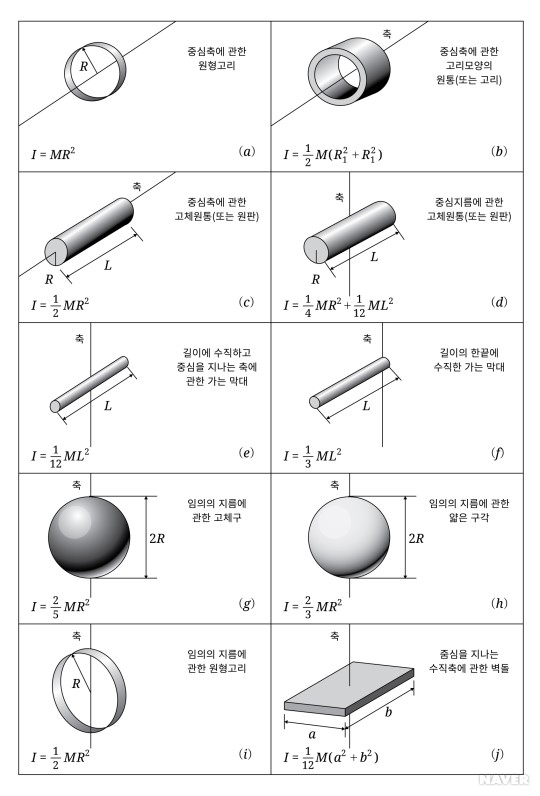
- 강체의 형태 및 회전축에 따른 관성 모멘트
그림 2는 빗면을 따라 굴러 내려가는 원기둥 모양의 강체를 그린 그림이다. 속이 꽉 찬 원기둥의 관성 모멘트는 ½mr² 이고, 여기서 m 은 원기둥의 질량, r 은 원기둥 밑면의 반지름이다. 회전하며 내려가는 원기둥의 운동을 분석할 때, 회전의 중심을 원기둥 밑면의 중심을 지나며 옆면에 평행한 축으로 할 때와 원기둥과 빗면이 접촉하는 선을 축으로 할 때, 평행축 정리에 따라 원기둥의 관성 모멘트가 달라진다. 회전축 1에 의한 관성 모멘트 I₁ 과 회전축 2에 의한 관성 모멘트 I₂ 의 관계는 평행축 정리에 의해 다음과 같다.
이제 원기둥의 질량중심을 회전축으로 정할 때와 원기둥과 빗면과의 접촉면을 회전축으로 정할 때 회전 에너지는 다르지만 총 운동 에너지는 여전히 같음을 보이자. 먼저, 물체는 빗면에서 마끄러지 않고, 물체의 질량중심이 속력 v 로 운동한다고 가정한다. 이때 선속도와 각속도의 관계에 의해 다음이 성립한다.
v = r ⍵ ⍵ = v/r
회전축 1을 기준으로 삼을 때는 회전 운동과 질량중심의 선운동이 동시에 존재하며, 각각의 에너지는 다음과 같다.
이는 질량중심이 속도 v→ 로 움직일 때 선운동에 의한 운동 에너지뿐만 아니라 회전운동에 의한 회전 에너지가 존재함을 명백히 보여준다. 이어서 회전축 2를 기준으로 삼을 때는 질량중심의 선운동 효과가 평행축 정리에 의해 관성 모멘트에 더해지므로 운동 에너지의 총량은 오로지 회전 에너지에 의존한다.
따라서 어떤 회전축을 설정하는지에 관계없이 물체의 에너지가 일정하다는 것을 알 수 있다.
참고자료
같이 보기

 위키원
위키원