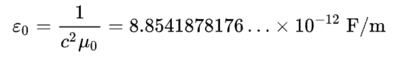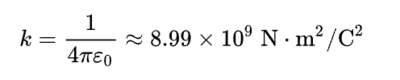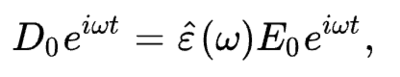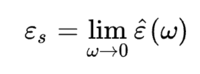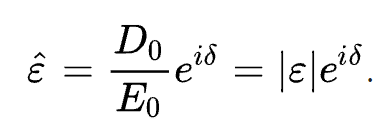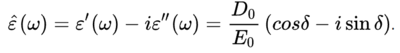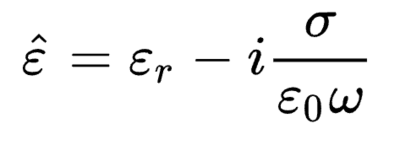"유전율"의 두 판 사이의 차이
잔글 |
잔글 (→= 물질의 분류) |
||
| 71번째 줄: | 71번째 줄: | ||
어떤 주파수에서 ℇ^의 허수부가 양수인 경우에는 에너지가 흡수되어 손실이 생기고, 음수인 경우에는 이득이 생긴다. 좀 더 일반적으로 말해서, 등방적이지 않은 경우 유전율 텐서 고윳값의 허수부를 무시하면 안 된다. | 어떤 주파수에서 ℇ^의 허수부가 양수인 경우에는 에너지가 흡수되어 손실이 생기고, 음수인 경우에는 이득이 생긴다. 좀 더 일반적으로 말해서, 등방적이지 않은 경우 유전율 텐서 고윳값의 허수부를 무시하면 안 된다. | ||
| − | + | == 물질의 분류 == | |
| − | + | [[물질]]은 그 물질의 유전율 ℇ과 [[도전율]] σ에 따라 분류할 수 있다. 금속의 경우 전자기파의 흐름을 방해하는데, 이때 일반적으로 σ/⍵ℇ>>1을 만족하고 이를 좋은 [[전도체]]로 분류한다. 반면 부도체의 경우 σ/⍵ℇ<<1이 성립한다. 이런 양극한에 속하지 않는 매질이 일반적인 매질이다. | |
"완전유전체"는 변위전류만 흐르는 물질이다. 따라서 이 물질은 마치 축전기처럼 전기 에너지를 저장하고 방출하기만 한다. 이런 물질이 아닌 매질에서 전도에 의한 전류가 무시할 수 없는 양이라면 손실이 생기는데, 이때 흐르는 전체 전류밀도는 다음과 같다. | "완전유전체"는 변위전류만 흐르는 물질이다. 따라서 이 물질은 마치 축전기처럼 전기 에너지를 저장하고 방출하기만 한다. 이런 물질이 아닌 매질에서 전도에 의한 전류가 무시할 수 없는 양이라면 손실이 생기는데, 이때 흐르는 전체 전류밀도는 다음과 같다. | ||
| 81번째 줄: | 81번째 줄: | ||
=== 유전체 흡수 과정 === | === 유전체 흡수 과정 === | ||
| − | 일반적으로 | + | 일반적으로 [[유전체]]가 [[전자기파]]의 [[에너지]]를 흡수하는 과정은 주파수에 따라 다양한 메커니즘으로 일어난다. |
* 완화 효과 : 분자의 영구쌍극자와 유도쌍극자 성질에 관련되어 있다. 낮은 주파수에서 장이 충분히 느리게 변한다면 쌍극자들은 장이 변하기 전에 평형에 도달할 수 있다. 쌍극자가 장의 변화를 따라가지 못할 만큼 매질의 점성이 크다면, 장의 에너지는 흡수되어 손실된다. 쌍극자가 완화되는 이러한 메커니즘을 일컬어 "유전완화(dielectric relaxation)"라 하고, 이상적인 쌍극자의 경우 고전적인 디바이 완화(Debye relaxation) 과정으로 설명할 수 있다. | * 완화 효과 : 분자의 영구쌍극자와 유도쌍극자 성질에 관련되어 있다. 낮은 주파수에서 장이 충분히 느리게 변한다면 쌍극자들은 장이 변하기 전에 평형에 도달할 수 있다. 쌍극자가 장의 변화를 따라가지 못할 만큼 매질의 점성이 크다면, 장의 에너지는 흡수되어 손실된다. 쌍극자가 완화되는 이러한 메커니즘을 일컬어 "유전완화(dielectric relaxation)"라 하고, 이상적인 쌍극자의 경우 고전적인 디바이 완화(Debye relaxation) 과정으로 설명할 수 있다. | ||
2021년 9월 30일 (목) 00:12 판
유전율(誘電率, Permittivity)은 유전체가 외부 전기장에 반응하여 만드는 편극의 크기를 나타내는 물질상수이며, 국제단위계에서의 단위는 F·m⁻¹이다. 유전율이 클수록 유전체는 큰 편극을 만들며 유전체 내부의 전기장은 작아진다.
개요
유전율 또는 전매상수는 전하 사이에 전기장이 작용할 때, 그 전하 사이의 매질이 전기장에 미치는 영향을 나타내는 물리적 단위이다. 매질이 저장할 수 있는 전하량으로 볼 수도 있다. 같은 양의 물질이라도 유전율이 더 높으면 더 많은 전하를 저장할 수 있기 때문에, (저장된 전하량이 동일할 때)유전율이 높을수록 전기장의 세기가 감소된다. 그래서 높은 유전율을 가진 물질을 축전기에 넣는 유전체로 사용하면, 축전기의 전기 용량이 커진다.
전자기학에서는 물질에 가해진 전기장 E가 얼마나 물질의 구성에 영향을 마치는지 나타내는 정도를 전기변위장(electric displacement field) D로 정의한다. 이 전기변위장 D와 유전율과의 관계는 다음과 같다.
D = ℇ ∙ E
유전율 ℇ은 매질이 등방성(isotropy)을 가질 때에는 스칼라이지만, 그렇지 않은 경우에는 3×3 행렬로 표현된다.
유전율은 실수일 수도, 복소수일 수도 있다. 일반적으로 유전율은 상수값이 아닌데, 이것은 유전율이 매질의 부분, 그 매질에 가해진 전자기장의 주파수, 습도, 온도 등과 같은 여러 요인에 의해 영향을 받기 때문이다.
국제단위계에서 유전율의 단위는 패럿/미터다. 전기변위장 D의 단위는 쿨롱/제곱미터 [C/m²]이고, 전기장 E의 단위는 볼트/미터 [V/m]다.
전기변위장과 전기장은 전하에 의해 발생하는 같은 현상을 나타낸다. 전기변위장은 전하의 전기 선속을 나타내는 데 유용하고, 전기장은 전기 선속 내의 단위 전하에 작용하는 힘을 측정하는 데 이용한다. 진공의 유전율 ℇ₀는 진공에서 이 둘 사이의 관계를 나타내는 변환값(scale factor)이다. ℇ₀는 국제단위계로 8.8541878176... ×10⁻¹² [F/m]이다.
진공의 유전율
물질의 유전율은 보통 상대 유전율, 즉 진공의 유전율에 대한 상대적인 값 ℇr로 나타낸다. 이 값을 흔히 유전상수(dielectric constant, 誘電常數)라고도 한다. 실제 유전율은 상대 유전율에다 진공의 유전율 ℇ₀를 곱해서 구할 수 있다.
ℇ = ℇrℇ₀
진공의 유전율 ℇ₀은 진공 상태에서 D/E' 값으로, 다음과 같이 정의된다.
여기서 c는 빛의 속도이고, μ₀ 는 진공의 투자율(permeability)이다. 이 세 값은 모두 SI 단위계에 정확히 정의되어 있다.
쿨롱의 법칙에서 나오는 쿨롱 힘 상수의 정의식에는, 이 진공의 유전율이 포함되어 있다. (쿨롱 힘 상수는 진공에서 단위 전하 두개가 단위 거리만큼 떨어져 있을 때 서로 작용하는 힘의 크기이다)
매질의 유전율
등방성을 가진 매질의 경우에는 D와 E가 평행 벡터고, 따라서 ℇ는 스칼라가 된다. 하지만 일반적으로 매질이 등방성을 갖지 않는 경우에 ℇ은 2차 텐서고, 이로 인해 복굴절 현상이 일어난다.
매질 속에서 전자기파의 위상속도 v는 물질의 유전율 ℇ'과 자기 투과율 μ 에 의해 다음과 같이 결정된다.
V²= 1/ℇμ 매질에 전기장이 가해지게 되면, 전류가 흐른다. 실제 매질을 통해 흐르는 전체 전류는 전도전류와 변위전류로 구성된다. 전도전류는 하전입자가 직접 전하를 전달하여 생기는 전류고, 변위전류는 물질이 전기장에 용수철처럼 탄성반응을 하는 것이라고 생각할 수 있다. 물질에 가하는 전기장을 세게 하면 물질에 저장된 변위전류는 증가하고, 전기장을 약하게 하면 물질에 저장된 변위전류가 줄어든다. 전기적 변위는 다음 식처럼 진공에 의한 항과 물질에 의한 항으로 나눌 수 있다.
P는 매질의 분극χ는 전기적 감수율(electric susceptibility)이다. 따라서 물질의 상대 유전율과 감수율은 다음과 같은 관계를 갖게 된다.
ℇr = χ + 1
복소수 유전율
진공과는 달리, 실제 물질이 외부 장에 반응할 때는 그 장의 주파수도 중요하게 작용한다. 이 현상은 물질이 가해진 장 자체에 반응하는 것이 아니라, 장이 가해진 이후 그에 따라 발생하는 일련의 변화에 반응함을 의미한다. 따라서 유전율은 단순한 상수 ℇ 가 아니라 외부 장의 주파수 ⍵에 대한 복소함수 ℇ^(⍵)로 나타나게 된다.
여기서 D₀와 E₀은 각각 변위 장과 전기장의 크기를 나타내고, i= √-1은 허수 단위이다.
정적인 전기장에 대한 매질의 반응은 위의 유전율에서 주파수를 0으로 극한을 취해서 표현할 수 있으며, 이 유전율을 "정적 유전율" 혹은 유전 상수 ℇs(또는 ℇDC라고 한다.
한편 주파수가 매우 큰 경우의 복소 유전율은 보통 ℇ∞라고 쓴다. 참고로 플라즈마 주파수 이상의 매우 큰 주파수에서는, 전자가 원자로부터 떨어져나와 기체처럼 운동하면서 유전체의 성질을 이상적인 금속과 같게 만든다.
정적 유전율(주파수 0)과 낮은 주파수로 진동하는 장에서의 유전율은 비슷한 값이고, 주파수가 점점 높아지면서 D와 E사이의 위상차 δ가 커지기 시작한다. 이 차이가 눈에 띄도록 나타나는 주파수는 온도와 물성에 따라 달라진다. 평균적인 장 세기 (E₀)에서 D와 E는 비례하고 다음과 같은 공식이 성립한다.
이렇게 장의 세기가 계속 변하는 경우 유전율은 복소 유전율이므로 다음과 같이 실수부와 허수부로 나눌 수 있다.
위 등식에서 ℇ´은 유전율의 실수부, ℇʺ은 유전율의 허수부이다. 이 허수부는 매질에 의한 에너지 흡수 속도와 연관되어 있다.
복소 유전율은 보통 주파수 ⍵ 에 관한 복잡한 함수로, 유전체가 주파수에 따라 다양하게 장을 흡수하기 때문이다. 하지만, 실제로 주파수 영역이 좁다면, 유전율은 주파수에 무관하거나 간단한 모델 함수로 근사할 수 있다.
어떤 주파수에서 ℇ^의 허수부가 양수인 경우에는 에너지가 흡수되어 손실이 생기고, 음수인 경우에는 이득이 생긴다. 좀 더 일반적으로 말해서, 등방적이지 않은 경우 유전율 텐서 고윳값의 허수부를 무시하면 안 된다.
물질의 분류
물질은 그 물질의 유전율 ℇ과 도전율 σ에 따라 분류할 수 있다. 금속의 경우 전자기파의 흐름을 방해하는데, 이때 일반적으로 σ/⍵ℇ>>1을 만족하고 이를 좋은 전도체로 분류한다. 반면 부도체의 경우 σ/⍵ℇ<<1이 성립한다. 이런 양극한에 속하지 않는 매질이 일반적인 매질이다.
"완전유전체"는 변위전류만 흐르는 물질이다. 따라서 이 물질은 마치 축전기처럼 전기 에너지를 저장하고 방출하기만 한다. 이런 물질이 아닌 매질에서 전도에 의한 전류가 무시할 수 없는 양이라면 손실이 생기는데, 이때 흐르는 전체 전류밀도는 다음과 같다.
여기서 σ는 매질의 도전율, ℇr는 상대 유전율을 의미하고, {\displaystyle \omega }\omega 는 가해진 장의 주파수를 의미한다. 이 가해진 장에 변화가 없는 경우, 즉 주파수가 0인 경우에는 변위전류가 흐르지 않는다. 또한 ℇ^은 복소 유전율로, 다음과 같이 정의된다.
유전체 흡수 과정
일반적으로 유전체가 전자기파의 에너지를 흡수하는 과정은 주파수에 따라 다양한 메커니즘으로 일어난다.
- 완화 효과 : 분자의 영구쌍극자와 유도쌍극자 성질에 관련되어 있다. 낮은 주파수에서 장이 충분히 느리게 변한다면 쌍극자들은 장이 변하기 전에 평형에 도달할 수 있다. 쌍극자가 장의 변화를 따라가지 못할 만큼 매질의 점성이 크다면, 장의 에너지는 흡수되어 손실된다. 쌍극자가 완화되는 이러한 메커니즘을 일컬어 "유전완화(dielectric relaxation)"라 하고, 이상적인 쌍극자의 경우 고전적인 디바이 완화(Debye relaxation) 과정으로 설명할 수 있다.
- 공명 효과 : 원자, 이온, 전자의 회전운동 혹은 진동운동으로 인해 발생한다. 이 과정은 각 운동의 해당 흡수 주파수 근처에서 나타난다.
유전율 측정
물질의 유전율은 다양한 정전기적 방법으로 측정할 수 있다. 복소 유전율은 10⁻⁶ 헤르츠에서 10¹⁵ 헤르츠에 달하는 다양한 주파수 범위에 대해 각기 다른 유전율 분광학 기법을 사용해서 측정한다. 또한 저온유지장치와 오븐을 이용하면 시간에 따라 특정 매질 속의 유전율이 어떻게 변하는지 측정할 수 있다. 여러 여기장들에 대해 계가 어떻게 반응하는지 보고 싶을 때는 특정 주파수 영역에서 다양한 측정 장치를 설치하여 측정한다.
- 저주파 시간 영역 측정 (10⁻⁶-103 [Hz])
- 저주파 주파수 영역 측정 (10⁻⁶-10⁶ [Hz]) - 일반적으로 많이 측정되는 영역이다. 평행판 축전기를 만들어서 그 전기용량(capacitance)를 임피던스 분석기를 이용하여 측정함으로써 주파수에 따른 유전율을 측정할 수 있다.
- 반사 동축 기법 (10⁶-10¹⁰ [Hz])
- 투과 동축 기법 (10⁸-10¹¹ [Hz])
- 유사광학(quasi-optical) 기법(10⁹-10¹⁰ [Hz])
- 푸리에 변환 기법 (10¹¹-10¹⁶ [Hz])
참고자료
- 〈유전율〉, 《위키백과》
같이 보기

 위키원
위키원