회전축(axis of rotation, rotation axis)은 회축의 고정축 또는 한 축의 주위로 한 도형이 회전하는 대칭조작이 이루어질 때, 그 축을 회전축, 회전대칭축 또는 간단히 대칭축이라고 한다.
2π/n(n은 자연수)의 회전으로써 완전히 같은 도형이 되풀이되는 성질을 회전대칭이라고 하고, n을 회전대칭의 차수 또는 회수, 그 회전축을 n회의 회전축 또는 n회축이라고 한다.
결정에 나타나는 대칭에 관하여는, n=1, 2, 3, 4, 6에 한한다.
n회축의 기호는 n이다.
넓은 뜻으로는 반전을 포함하는 회전반전축, 회영축가지 넣어 일컫는다.
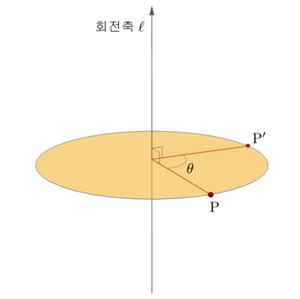
차원 유클리드 공간의 유향직선 을 중심으로 의 방향으로 엄지손가락을 향하게 하고 오른손의 나머지 네 손가락을 쥐었을 때, 이 네 손가락이 감아서 가리키는 방향으로 일정한 각 만큼 회전하는 변환을 직선 을 중심으로 하는 회전변환이라 하고, 이때 을 이 회전변환의 회전축이라고 한다.
회전축 위의 모든 점은 회전변환에 의하여 움직이지 않는다. 또한 회전변환이 항등변환이 아니라면, 회전축 위에 있지 않은 점은 모두 회전변환에 의하여 움직인다. 그러므로 회전축은 항등변환이 아닌 회전변환에 의하여 움직이지 않는 점인 회전변환의 고정점을 모두 모아 놓은 집합이다.
차원 유클리드 합동변환에는 평행변환, 회전변환, 스크류변환, 대칭변환, 미끄럼변환, 회전대칭변환의 가지 형태의 변환이 있는데, 이중 모든 고정점을 모아 놓은 집합이 직선이 되는 변환은 회전변환뿐이다.
참고자료[편집]
같이 보기[편집]
|
 이 회전축 문서는 에너지에 관한 토막글입니다. 위키 문서는 누구든지 자유롭게 편집할 수 있습니다. [편집]을 눌러 이 문서의 내용을 채워주세요.
|
| 산업 : 산업, 산업혁명, 기술, 제조, 기계, 전자제품, 정보통신, 반도체, 화학, 바이오, 건설, 유통, 서비스, 에너지 □■⊕, 전기, 소재, 원소, 환경, 직업, 화폐, 금융, 금융사, 부동산, 부동산 거래, 부동산 정책, 아파트, 건물, 토지
|
|
|
| 에너지
|
SMR • 가속운동 • 가시광선 • 가열 • 각속도 • 감마선 • 감속운동 • 강력 • 고압 • 고온 • 고전역학 • 관성력 • 관성모멘트 • 광선 • 광속 • 광전자 • 광전효과 • 광합성 • 기압 • 냉각 • 냉방 • 뉴턴 • 대류 • 대체에너지 • 동력 • 동력원 • 라디오파 • 마이크로파 • 마찰 • 마찰계수 • 마찰력 • 마찰에너지 • 만유인력 • 만유인력의 법칙 • 무중력 • 물리에너지 • 바이오에너지 • 발열 • 발열반응 • 발화 • 방사선 • 방열 • 베타선 • 복사 • 복사선 • 복사에너지 • 부력 • 불 • 블루에너지 • 빛 • 빛에너지 • 삼투압 • 생물에너지 • 석유에너지 • 석탄에너지 • 섭씨 • 소리에너지 • 소수력 • 속력 • 수력 • 수력에너지 • 수소에너지 • 수압 • 수열 • 수열에너지 • 수직항력 • 신생에너지 • 신에너지 • 신재생 • 신재생에너지 • 알짜힘(합력) • 알파선 • 압력 • 압축응력 • 약력 • 양극선 • 양자역학 • 에너지 • 에너지밀도 • 에너지보존법칙 • 에너지원 • 에너지 효율 • 엑스선 • 엔트로피 • 역반응 • 역파장 • 역학적 에너지(기계에너지) • 열 • 열대류 • 열량 • 열복사 • 열분해 • 열에너지 • 열역학 • 열전도 • 열전도도 • 열전도율 • 열절연 • 열팽창 • 열팽창계수 • 열효율 • 온도 • 온도차 • 왕복에너지 • 왕복운동 • 운동에너지 • 원운동 • 원자력 • 원자력에너지 • 위치에너지 • 음극선 • 응력 • 인공태양 • 인장응력 • 인화 • 입자선 • 자외선 • 자유낙하 • 작용 • 재가열 • 재생에너지 • 저온 • 저압 • 적외선 • 전기에너지 • 전도 • 전자기력 • 절대온도 • 정반응 • 정지에너지 • 조력 • 조력에너지 • 조류에너지 • 줄 • 줄의 법칙 • 중력 • 중력에너지 • 지열 • 지열에너지 • 직사광선 • 직선운동 • 진동 • 진동에너지 • 진자 • 진자운동 • 천연에너지 • 청정에너지 • 친환경에너지 • 칼로리 • 탄성 • 탄성에너지 • 태양 • 태양광 • 태양광에너지 • 태양에너지 • 태양열 • 태양열에너지 • 텐서 • 파동 • 파력 • 파력에너지 • 파워 • 파장 • 폐기물에너지 • 폭발 • 풍력 • 풍력에너지 • 풍압 • 항력(드래그포스) • 해양에너지 • 핵반응 • 핵분열 • 핵분열에너지 • 핵붕괴 • 핵에너지 • 핵융합 • 핵융합에너지 • 화력 • 화씨 • 화학 • 화학에너지 • 회전 • 회전수 • 회전에너지 • 회전운동 • 흡열 • 흡열반응 • 힘
|
|
|
| 발전
|
교류발전기 • 마이크로 수력발전 • 물레방아 • 박테리아 발전소 • 발전 • 발전기 • 발전소 • 발전효율 • 변전소 • 비상발전기 • 소수력발전 • 소수력발전소 • 소형모듈원전(SMR) • 수력발전 • 수력발전소 • 원자력발전 • 원자력발전소 • 조력발전 • 조력발전소 • 조류발전 • 조류발전소 • 지열난방 • 지열발전 • 지열발전소 • 직류발전기 • 태양광발전 • 태양광발전소 • 태양광패널 • 태양열발전 • 태양열발전소 • 파력발전 • 파력발전소 • 풍력발전 • 풍력발전소 • 풍차 • 해양 온도차 발전 • 핵융합발전 • 핵융합발전소 • 화력발전 • 화력발전소 • 회전축
|
|
|
| 연료
|
CNG • LNG • LPG • 가스 • 가스충전소 • 가연성 • 갈탄 • 개질수소 • 경유(디젤) • 경질유 • 고급휘발유 • 고압가스 • 고체연료 • 그레이수소 • 그린수소 • 기체연료 • 나무 • 난방연료 • 두바이유 • 등유 • 땔감 • 면세유 • 무연탄 • 무연휘발유 • 바이오 • 바이오가스 • 바이오디젤 • 바이오매스 • 바이오에탄올 • 바이오연료 • 방사성물질 • 배기가스 • 배출가스 • 번개탄 • 부생수소 • 분별증류 • 뷰테인(부탄) • 브라운수소 • 브렌트유 • 블루수소 • 석유 • 석유화학 • 석탄 • 셰일가스 • 셰일오일 • 수소 • 수소연료 • 수소전기 • 순도 • 숯(목탄) • 압축가스 • 액체연료 • 액화가스 • 역청탄 • 연료 • 연료첨가제 • 연료화 • 연비 • 연소 • 연탄 • 오일샌드 • 오일셰일 • 옥탄가 • 용해가스 • 원유 • 유사경유 • 유연탄 • 유연휘발유 • 윤활유 • 일반휘발유 • 장작 • 점화 • 정유 • 정제 • 조개탄 • 주입 • 중유 • 중질유(中質油) • 중질유(重質油) • 증류 • 질소산화물 • 천연가스 • 천연자원 • 친환경연료 • 코크스 • 타르 • 텍사스유 • 프로페인(프로판) • 합성경유 • 핵연료 • 혼유 • 혼합가스 • 혼합기체 • 혼합연료 • 화석연료 • 화재 • 휘발유(가솔린)
|
|
|
| 위키 : 자동차, 교통, 지역, 지도, 산업, 기업, 단체, 업무, 생활, 쇼핑, 블록체인, 암호화폐, 인공지능, 개발, 인물, 행사, 일반
|
|
위키원
