전하
전하(電荷, electric charge)는 전자기장 내에서 전기현상을 일으키는 주체적인 원인이다. 특히 공간에 있는 가상의 점이 갖는 전하를 점전하라고 하고, 전하의 양을 전하량(Q)이라고 한다. 전하의 국제단위는 쿨롱이며, 단위기호는 C이다. 1 쿨롱은 매우 큰 단위이며, 약 6.25×10¹⁸개의 전자나 양성자들의 전하량이다. 반대로, 전자 또는 양성자 한 개의 전하량은 1.6021773349 ×10⁻̦¹⁹ 쿨롱이며, 이를 기본전하라고 부른다. 전하는 음의 전하와 양의 전하가 있다. (이는 질량과 같이 양의 값만 있는 다른 물리량과 다르다.) 통상적으로 양성자나 양전자 따위의 전하를 양으로, 전자 등의 전하를 음으로 놓는다.
개요
전하는 전기 현상을 일으키는 물질의 물리적 성질이다.
일상 생활에서 쉽게 목격할 수 있는 전기 현상으로 플라스틱 봉을 천에 문질렀을 때 생성되는 각각의 물질이 전기적 성질, 즉 전하를 띠게 되고 이 들 사이에 밀고 당기는 현상을 관측함으로써 그 존재를 확인할 수 있다. 이 때 서로 미는(척력) 경우가 있고, 또 서로 당기는(인력) 경우도 있어 두 종류의 전하가 있음을 알 수 있다. 프랭클린(B. Franklin, 1706-1790)은 두 종류의 전하를 양(+) 전하와 음(-) 전하라고 이름 지었다.
일상 생활에서 전기 현상을 쉽게 느끼지 못하는 것은 이 두 종류의 전하가 같은 양 만큼 있어 서로의 효과가 상쇄되기 때문이다. 밀리컨(R. Millikan, 1868-1953)은 1909년에 모든 전하는 기본전하량 의 정수배로 존재한다는 사실을 발견하였다. 한편 자연계의 모든 물질이 원자로 만들어져 있고 이 원자는 중심의 원자핵과 주변의 전자로 구성되어 있다는 것이 알려졌다. 또 원자핵은 전하를 가진 양성자와 전기적으로 중성인 중성자로 구성되어 있다는 점도 알려졌다. 이 때 전자와 양성자는 기본전하량 e를 갖고 있는데 전자는 음전하(-e)를 양성자는 양전하(+e)를 가진다. 보통의 원자는 같은 수의 양성자와 전자를 갖고 있어 전기적으로 중성을 띤다. 앞의 경우처럼 두 물체를 문지르는 경우 음전하를 띤 많은 수의 전자가 한 쪽에서 다른 쪽으로 움직이고 전자가 많아 진 쪽은 음전하를 전자를 없어진 쪽은 양전하를 띠게 된다.
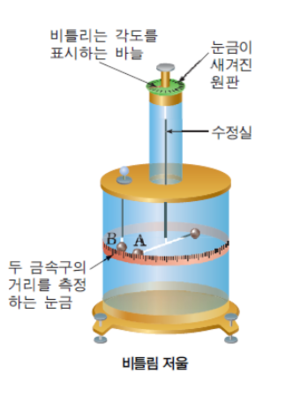
전하를 띤 입자 사이에 작용하는 힘은 쿨롱의 법칙을 따른다. 쿨롱(C.-A. de Coulomb, 1736-1806)은 자신이 발명한 비틀림 저울을 사용하여 전기를 띤 물체 사이의 전기력에 대한 실험을 수행하였다 (오른쪽 그림). 그 결과 두 전하 사이에 작용하는 힘이 두 전하의 거리의 제곱에 반비례하고 두 전하량의 곱에 비례한다는 것과, 음전하-음전하 혹은 양전하-양전하와 같이 같은 종류의 전하는 서로 밀고, 양-음전하와 같이 다른 종류의 전하는 서로 당긴다는 것을 발견하였다. 이 결과를 다음의 식으로 표시 할 수 있다.
F = k ·q₁q₂/r²
여기서 , q₁q₂는 각각의 전하, k는 쿨롱 상수를 표시한다.
역사
전기에 의한 전하의 개념은 라이덴 병의 관련성까지도 거슬러 올라갈 수 있고, 그 이전의 고대 그리스 시대에도 이미 호박을 문지르면 옷자락이나 먼지 같은 것들이 달라붙는 현상으로부터 통해 정전기의 존재는 현상을 관찰하는 관념적인 수준으로나마 알고 있었다.
애초에 전기와 관련된 용어들, 특히 전하(electron)의 경우에는 호박을 뜻하는 고대 그리스어 엘렉트론(ήλεκτρον)로부터 기원한 단어이다. 이후 18세기 중엽에 미국의 건국의 아버지이자 발명가인 벤자민 프랭클린(Benjamin Franklin, 1706-1790)은 뇌우 속으로 연을 날리는 실험을 통해, 호박에 의해 발생되는 것과 번개가 본질적으로 동일한 것임을 입증했다.
도체(conductor) 위에서, 정전하량 Q의 관계식은 전기용량(capacitance) C와 전위(potential) V에 의해 정해지고 그 식은 다음과 같다.
Q=CB(정전하량 관계식)
이는 최초로 화학 전지를 만들어낸 알레산드로 볼타(Alessandro Volta, 1745-1827)에 의해 정립된 것이다. 그리고 전기적인 물질의 축적, 즉 에너지량으로서의 전하 개념은 앞서 말했듯 18세기 후반에 쿨롱(Charles Augustin de Coulomb)에 의해 정립되었고, 1820년에는 전기가 흐르는 도선인 전선이 자침(magnetic needle)에 힘을 미친다는 사실이 밝혀져 전기와 자기의 개념이 형성되기 시작했다. 이로 인해 물리학자들은 전하에 대한 두 가지 측정법을 알게 되었으며, 하나는 정지해 있는 전기인 정전기(electricity at rest, static electricity)이고, 다른 하나는 움직이는 전기인 동전기(electricity in motion, electromagnetic)에 대한 것이다. 이 중에서 동전기는 일반적인 전기와 같은 것이므로 잘 쓰이지는 않는 용어다.
1857년에 베버(Wilhelm Weber)와 콜라우쉬(Rudolph Kohlrausch)가 처음으로 측정 비율에서 정밀 값을 얻어냈는데, 이 두 사람이 얻어낸 값은 광속에 매우 가까운 값으로 그 값은 다음과 같았다.
3.1074 ×10¹⁰cm sec⁻¹ 이후에 맥스웰(James Clerk Maxwell)은 그의 이론을 통해 전류의 속도가 진공 상태에서의 광속과 정확히 같다는 것을 증명해냈고, 1833년에는 패러데이(Farady)의 전기 분해 법칙에 의해, 전기 분해시 전극에서 방출되는 이온(ion)들이 옮기는 전하량이 기본 단위 전하량의 작은 정수배로만 이루어진다는 것이 암시되었다.
1881년 헬름홀츠(Hermann von Helmholtz)에 의해 물질이 원자로 구성되어 있다면 전기도 마찬가지일 것이라는 이론이 제기되었고, 스토니(G.J. Stoney)에 의해 전기원자의 전하량에 전자(electron)라는 명칭이 주어졌다. 이후 1897년에 J.J 톰슨(J.J. Thompson)이 전자를 처음으로 발견함으로써 전자의 전하량 측정이 가능해졌다.
전하 방울 모음(collecting charged droplets) 값에 의해 톰슨이 표준값을 얻어냈으며, 이후 밀리칸(Robert A. Millikan)이 유사한 방법으로 더 정밀한 값을 얻어냈다. 러더포드(Rutherford)와 가이거(H. Geiger)는 알고 있는 α 입자의 수로부터 그곳에 붙어있는 전체 전하를 측정할 수 있었고, 밀리칸과 러더포드가 얻어낸 값은 대략 다음과 같았다.
4.7 ×10⁻¹⁰cm e.s.u
이 값은 근사적인 값에다 러더포드와 가이거가 개별적으로 측정한 값이지만 둘의 결과가 거의 일치하고 있었고, 이는 플랑크(Planck)의 방사법칙으로도 추론을 할 수 있었다. 이를 이용해 보어(Bohr)는 발머 공식으로부터 양자론에 중요한 공헌을 하게 된다.
전하의 구분
원자는 전자와 양성자, 중성자로 나눌 수 있으며, 전자는 음전하를 띠고 있고 양성자는 양전하를 띠고 있다. 전하는 이 양전하와 음전하로 나눌 수 있으며, 동일한 부호의 전하 사이에는 서로 밀어내는 척력이 작용하고, 다른 부호의 전하 사이에는 서로 잡아당기는 인력이 작용한다. 이는 마치 자기력의 인력/척력과 유사하다.
물체가 양전하 또는 음전하를 띠게 되는 이유는 기본 입자의 전하 때문이며, 전자는 음전하를 띠는 만면 양성자는 두 개의 위 쿼크(up quark)와 하나의 아래 쿼크(down quark)로 이루어져 양전하를 띤다.
일반적으로 원자는 양성자와 전자의 수가 균형을 이루어 전기적으로 중성인 상태에 있으나, 원자의 가장 바깥 껍질에 위치한 전자는 상대적으로 약하게 결합되어 있기 때문에 마찰력과 외부에서 작용하는 힘에 의해 쉽게 원자에서 벗어나게 된다. 이렇게 물질과 물질 사이에 전자들이 이동하게 되면서 전자를 잃은 쪽 물질은 양전하를 띠게 되고, 반대로 전자를 얻은 쪽의 물질은 음전하를 띠게 된다.
전하의 단위
전하의 양은 전하량(전기량; quantity of electron charge)으로 불리며, 단위는 C(쿨롱, Coulomb)이다. 이는 쿨롱의 법칙을 발견한 샤를 드 쿨롱의 이름을 그대로 따온 것이다. 쿨롱의 법칙은 금속공과 비틀림 저울을 이용하여 두 점전하 사이에 작용하는 힘을 측정하여 발견한 법칙으로, 두 전하 사이에서 작용하는 힘은 두 전하 크기의 곱에 비례하고 거리의 제곱에는 반비례한다는 것이다.
단위로서의 쿨롱은, 도선에 1A의 전류가 흐를 때, 1초 동안 전선을 통과하는 전하량을 1C으로 정의하고, 그 값은 다음과 같다.
e ≅ 1.602 ×10⁻¹⁹ C
위의 전하량은 기본전하량으로서, 양자화된 값이므로 물체의 전하량은 기본전하량의 정수배 값을 갖게 된다. 하지만 기본전하량이 매우 작은 값이므로, 일반적으로는 양자화와 정수배 개념을 제외하고 그 값을 기입하기도 한다.
일반적으로 전하를 표현하는 기호는 q로서, 극성에 따른 구분은 다음과 같이 한다.
단일 양성자의 전하량 qp = +e
단일 전자의 전하량 qe = -e
일정 구간의 전하는 '순전하'라고 하며, 이는 주어진 공간에서 존재하는 모든 양성자와 전자의 전하량 차이와 같다. 이 때문에 전하량을 항상 e의 정수배로 표현하는 것이다.
또한 다음과 같은 사실도 알 수 있다.
1C = 약 6.25 ×10¹⁸개의 양성자가 모였을 때 전하량
위와 반대로, 같은 개수의 전자가 모였을 때에는 전체 전하량이 -1C가 된다. 그러나 보통 쿨롱 값을 계산 상에 대입할 때에는 전하량의 크기를 대입하는 목적으로 절대값을 취해서 쓴다. (이러한 혼동을 막기 위해서, 보통 전자의 전하량은 의미를 명확하게 하기 위해 -e로 표기한다.)
여담으로 고립계에서는 전하량 보존 법칙이 성립하는데, 이는 맥스웰 방정식으로 유도할 수 있다.[1]
- 전하량 보존 법칙
전하는 생성되거나 소멸되지 않는다.
닫힌 계의 알짜 전하량은 어떠한 물리적인 변화를 겪더라도 항상 일정한 값을 유지한다. 즉 전하량이 보존되는 것이다. 이는 애초에 플랭크린(Benjamin Franklin)이 1747년에 처음으로 제안하였으며 물리의 가장 기본적인 법칙의 하나이다. 이 법칙은 대전입자가 에너지로 바뀌고 완전히 소멸하는 경우에도 성립해야 한다. 따라서 전자 하나가 고스란히 없어지는 경우는 전하량보존법칙에 위배되기 때문에 다른 선택으로서 - 전하를 가진 전자와 +전하를 가진 양전자가 함께 사라지는 선택을 할 수밖에 없다.
각주
- ↑ Fallen, 〈(전기/전자) 전하(electron charge)〉, 《네이버 블로그》, 2017-10-07
참고자료
같이 보기

 위키원
위키원