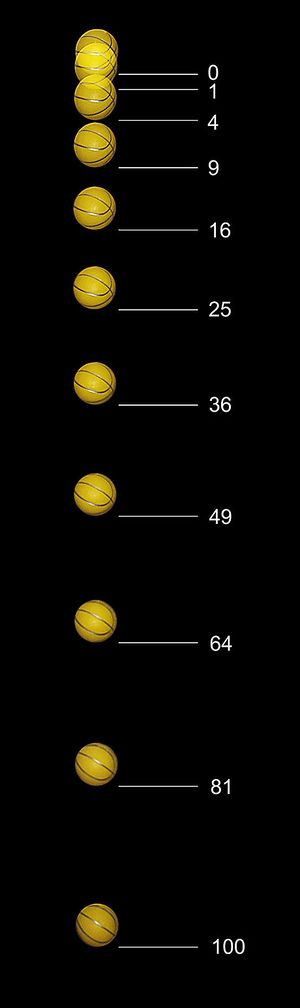
자유낙하
자유낙하(free fall)는 일정한 높이에서 정지하고 있는 물체가 중력의 작용으로 떨어질 때의 운동을 말한다. 고전역학에서 자유낙하는 오직 중력만이 작용하는 물체의 운동을 일컬으며, 일반상대이론에서는 아무런 힘이 작용하지 않는 물체가 시공간의 지름길(geodesic)을 따라가는 운동을 자유낙하라고 일컫는다.
낙하는 통상적으로 밑으로 향하는 운동을 의미한다. 하지만 뉴턴역학의 자유낙하는 중력의 방향에 따라 반드시 밑을 향하지 않을 수도 있다. 예컨대 달의 궤도가 지구를 향하지는 않지만 달은 자유낙하를 하고 있다.
또 다른 힘이 존재하지 않는 균일한 중력장에서, 한 물체에 작용하는 중력은 물체 어느 부분에서나 일정하다. 이와 같은 상황을 무중력 상태라고 하는데, 이것은 중력장이 영(0)인 상황과 동일하다. 자유낙하 하는 물체의 참가속도(proper acceleration)는 영(0 g)이다.
일상적으로는 "자유낙하"가 위에서 언급한 엄격한 의미로 쓰이지 않는 경우도 있다. 낙하산이나 부양 장치 없이 물체가 대기에서 낙하할 때 자유낙하한다고 말하기도 한다. 이 경우 공기의 저항은 완전한 무중력 상태를 만들지 못하게 한다. 따라서 종단 속력(terminal speed)에 도달한 스카이다이버는 자신의 무게가 공기의 저항력에 떠받쳐지는 느낌을 받게 된다.
자유낙하의 보편성과 등가원리
자유낙하를 하는 물체의 가속도는 물체의 질량과 관계없이 동일하다. 이를 "자유낙하의 보편성(universality of free-fall)"이라고 부른다. 알버트 아인슈타인(A. Einstein, 1879-1955)은 관성질량과 중력질량이 동일하다는 가정에서 출발하여 일반상대론을 전개했다. 이 가정을 때때로 "갈릴레이 등가원리(Galilean equivalence principle)", 혹은 "약한 등가원리(weak equivalence principle)"라고 부른다. 이 원리의 가장 중요한 결과는 자유낙하 하는 물체에 적용된다. 관성질량과 중력질량이 각각 , 인 물체를 고려하자. 자유낙하 하는 동안 이 물체에 작용하는 힘이 오직 중력장()에서 온다면, 뉴턴의 제이법칙과 중력의 법칙을 결합하여 다음과 같이 물체의 가속도를 얻을 수 있다:
a = M/m ∙ g
이것은 중력질량과 관성질량의 비가 어떤 상수 K가 되기 위한 필요충분조건이, '자유낙하 하는 모든 물체의 가속도가 질량에 무관하게 동일하다'인 것을 의미한다. 비 값인 가 상수이면 단위를 적절히 정의하여 이 값이 1이 되게 할 수 있다.
중력에 의한 자유낙하
일반적으로 자유낙하 운동은 물체가 지표 부근에서 오직 중력만을 받으며 낙하하는 운동을 말한다. 완벽한 자유낙하는 다른 외력이 전혀 존재해서는 안되지만 현실에서는 공기저항이나 지구의 자전에 의한 관성력과 같은 다른 힘을 받게 된다. 또한, 엄밀히 말해서 뉴턴의 만유인력을 적용하면 지구의 중력은 지구 중심에서 지표보다 떨어져 있을 경우 중심거리의 제곱에 반비례한다.
F = G ∙ Mm/r² G: 만유인력상수, M : 지구질량, m : 물체질량, r : 중심거리
중력 가속도(g)는 다음과 같다.
g = G ∙ M/r²
즉, 거리에 따라 가속도 값이 달라진다. 그러나 일반적으로 우리가 관찰하는 물체는 지구 전체 크기로 보았을 때 낙하하고 있다고 해도 거리 변화가 거의 없는 것이나 마찬가지로 가속도 역시 일정하다고 할 수 있다. 지표에서 가속도는 g = 9.8m/s²= 32.2ft/s² 으로 일정하다고 본다.
속도와 변위
질량을 가진 물체의 속도는 가속도를 시간에 대해 적분한 값으로 구할 수 있다. 이 경우에는 가속도가 상수함수의 꼴이므로 적분하면
v = v₀ + gt 그러나 초기 속도 v_0가 0임을 고려하면 v = gt 이다. 가속도를 적분하여 속도를 구했듯이 속도를 적분하면 변위를 구할 수 있다. 변위를 구할 때 유의할 점은 어디를 +방향으로 잡을 것인가 그리고 처음 변위는 얼마인가이다. 처음 변위를 S₀ 라 하고 중력 방향을 +로 놓자(사실 어느 방향을 +로 놓는지는 상관이 없다). 속도를 시간에 대해 적분하면 적분상수는 처음 변위인 S₀ 가 되므로
S = S₀ + ½gt² 라 할 수 있다.
평면에서 자유 낙하 운동
평면에서 xy좌표 평면을 생각할 때 중력이 -y방향으로 작용한다고 가정하자. 임의의 질량을 가진 물체가 x축 방향으로 등속운동을 한다면 중력의 영향을 받아 어떻게 운동할까?
x, y축의 운동은 서로 별개의 운동으로 생각해 줄 수 있다. x축 방향의 운동 상태가 어떠하던지 y축 방향의 운동( 여기서는 자유낙하 운동이라 하자)에는 영향을 주지 못한다. y축 방향은 중력에 의해 계속 가속되지만 x축 방향은 가속도가 0인 것이다.
역사
아리스토텔레스(Aristotle, B.C.384-B.C.322) 이후로 오랫동안 자유낙하에 대한 잘못된 편견이 있었다. 그것은 동일한 조건에서 무거운 물체가 가벼운 물체보다 더 빨리 낙하한다는 것이었다. 하지만 16세기에 이르러 갈릴레이(G. Galillei, 1564-1642)는 아리스토텔레스의 이 같은 주장을 실험과 관찰의 방법으로 반증하였다. 그는 전례 없었던 방식으로 실험 결과들을 수학적으로 분석하기도 했다.
물체의 낙하 시간이 질량에 의존하지 않는다는 것을 보이기 위해, 갈릴레이는 같은 물질로 만들어졌지만 질량이 다른 두 물체를 떨어뜨렸다. 그리고 실험으로부터의 결론을 뒷받침하기 위해 다음과 같은 논리를 전개했다: 질량이 다른 두 물체가 떨어지는 정도(가속도)가 다르다고 하자. 즉, 질량이 큰 물체가 더 빨리 떨어진다고 하자. 그런 후 이번에는 이 두 물체를 끈으로 묶어서 같이 떨어뜨려보자. 끈으로 묶인 두 물체는 질량이 더 커졌기 때문에 더 빨리 떨어져야 할 것이다. 한편, 두 물체 중 무거운 물체는 가벼운 물체에 의해 떨어지는 속도가 느려지게 되므로, 끈으로 묶인 두 물체는 무거운 물체 하나보다 더 천천히 떨어져야 할 것이다. 결론적으로, 이 두 가지 예상은 양립할 수 없으며, 따라서 질량에 따라 속도가 다르다는 것은 옳지 않다.
참고자료
같이 보기

 위키원
위키원