"공간"의 두 판 사이의 차이
leejia1222 (토론 | 기여) |
|||
| (사용자 3명의 중간 판 65개는 보이지 않습니다) | |||
| 1번째 줄: | 1번째 줄: | ||
| − | '''공간'''(space, 空間)은 어떠한 물질 또는 물체가 존재할 수 있거나 어떠한 일이 발생할 수 있는 장소이다. 사람이나 사물이 차지 하는 장소 또는 인간의 활동이 행해지는 장이나 | + | '''공간'''(space, 空間)은 어떠한 [[물질]] 또는 물체가 존재할 수 있거나 어떠한 일이 발생할 수 있는 장소이다. 사람이나 사물이 차지 하는 장소 또는 인간의 활동이 행해지는 장이나 [[물체]]의 운동이 그 속에서 전개되는 넓이를 의미하기도 한다. 공간은 물질이 존재하고 여러 가지 현상이 일어나는 장소이다.<ref name = "위키">〈[https://ko.wikipedia.org/wiki/%EA%B3%B5%EA%B0%84 공간]〉, 《위키백과》</ref><ref name = "나무">〈[https://namu.wiki/w/%EA%B3%B5%EA%B0%84 공간]〉, 《나무위키》</ref><ref name = "네이버사전">〈[https://terms.naver.com/entry.naver?docId=1717441&cid=41908&categoryId=41972 공간]〉, 《네이버 지식백과(현상학 사전)》</ref> 공간에서 특정 위치는 [[가로]], [[세로]], [[높이]]의 3가지 좌표를 이용해 표시할 수 있다. 이런 점에서 공간을 [[3차원]] 공간이라고도 한다. |
==개요== | ==개요== | ||
| − | 공간의 성질에 대한 이해를 시도하는 것은 | + | 공간의 성질에 대한 이해를 시도하는 것은 [[철학자]]와 [[과학자]]들에게 항상 어려운 숙제였다. 많은 토론의 결과에도 불구하고 공간에 대한 논쟁은 끊임없으며, 명확하고 확실한 정의를 제공하는 것은 어려운 일이다. 공간은 [[물리학자]], [[철학자]], [[수학자]], [[종교인]]에 의해 다양하게 다루어지고 공간과 마음 사이의 관계에서도 다양한 관점이 있다. 더불어 다양한 공간의 존재 방식이 있다는 것을 알 수 있다.<ref name = "나무"></ref> |
==공간의 존재 방식== | ==공간의 존재 방식== | ||
| 8번째 줄: | 8번째 줄: | ||
{{테두리색|#fff0f5|*고대 원자론자 : 아무것도 없는 공허한 것이다. | {{테두리색|#fff0f5|*고대 원자론자 : 아무것도 없는 공허한 것이다. | ||
| − | *데카르트 : 연장, 넓이가 물체의 본질이기 때문에 물체와 공간은 동일한 것이다.(이러한 생각에서 기하학과 물리학이 동일화된다.) | + | *[[데카르트]] : 연장, 넓이가 물체의 본질이기 때문에 물체와 공간은 동일한 것이다.(이러한 생각에서 기하학과 물리학이 동일화된다.) |
| − | *아리스토텔레스 : 공간은 사물들이 인접하는 경계, 따라서 사물을 받아들이는 용기와 같은 것인 장소의 총화이다. | + | *[[아리스토텔레스]] : 공간은 사물들이 인접하는 경계, 따라서 사물을 받아들이는 용기와 같은 것인 장소의 총화이다. |
| − | *뉴턴 : 일체의 부분 공간이나 상대 | + | *[[뉴턴]] : 일체의 부분 공간이나 [[상대 운동]]이 그것과의 연관에서 규정되는 유일한 기준으로서의 절대 공간이 존재한다. |
| − | *라이프니츠 : 공간은 물체와 독립하여 존재하지 않고 사물과 사물의 상호 관계의 총체에 지나지 않는다. | + | *[[라이프니츠]] : 공간은 물체와 독립하여 존재하지 않고 사물과 사물의 상호 관계의 총체에 지나지 않는다. |
| − | *칸트 : 공간을 초월론적 주관의 직관 형식으로 하여 뉴턴과 라이프니츠의 생각의 조정을 시도했다. | + | *[[칸트]] : 공간을 [[초월론적]] 주관의 직관 형식으로 하여 뉴턴과 라이프니츠의 생각의 조정을 시도했다. |
}} | }} | ||
| − | 위의 주장들과 관련하여 공간은 유한한가 무한한가 또 등질, | + | 위의 주장들과 관련하여 공간은 유한한가 무한한가 또 [[등질]], [[등방]]인가 아닌가와 같은 것도 논의가 있었지만, 주목을 끈 것은 고대와 중세에는 이 우주 공간이 지구를 중심으로 하여 항성천에 의해 한계 지어진 유한한 세계고 나아가 달 아래의 세계는 천상의 세계와 질적으로 다르고 무거운 물질이 중심을 향하는 것으로 특징이 지어짐으로써 공간에 방향성이 주어진 데 반해, 근세의 과학의 견해에서는 공간이 등질적이며 무한한 것으로 보았다. 19세기에 확립된 전자장 이론에서는 공간의 이질 이방성이 다시 제기되었고 아인슈타인의 일반 상대성 이론에서는 이 세계의 유한성이 주목되었다. 더불어 기하학과 물리학의 일체화라는 데카르트적인 생각이 다시 알려지며 재평가 되었다.<ref name = "네이버사전"></ref> |
| + | |||
| + | ===인간과 그 활동=== | ||
| + | 인간과 인간의 활동 존재 방식과 관련하여 공간은 [[생활공간]], [[도시공간]], [[환경 공간]] 등으로서 물체와 그 운동에 관련된 공간과 다르게 정의적 가치와 결부된 의미 공간을 규정된다. 예를 들어서 사람과 사람의 대면 상의 거리는 물질적인 거리에만 멈추지 않고 인간관계의 친소, 사회 신분상의 차이에 따라 변하는 심리적 거리도 반영한다. 지각 심리학이나 문화 인류학의 깨달음과 인간과 동물의 행동 양식은 같고 다름과 같은 정신병리학적 현상 등에 대한 고찰로부터 인간적 공간의 특성이 다양하게 제시되어 왔다.<ref name = "네이버사전"></ref> | ||
| + | |||
| + | ==현상학에서의 공간== | ||
| + | [[현상학]]에선 공간도 인간의 존재 방식과 상관적으로 다루어지기 때문에 인간적 공간만이 의미 공간인 것이 아닌 물리학적 공간, 수학적 공간도 인간의 의식에 의해 구성된 의미 공간이라고 칭한다. 공간의 의미의 중층적 구조가 분석, 해명되는데 여기선 공간이 지각된다. 그로 인해 행동이 행해지는 구체적 공간과 이념화하는 추상에 의한 극한 개념(점, 선, 면 등)이 설정되어 이것을 기초로 하여 전개되는 이념적 공간이 구별된다. [[구체적 공간]]은 기저층으로 공간적 위상을 기초로 하여 구성되고 이념적 공간은 기호를 매개로 하여 형식화하는 조작에 의한 형식적 수학적 공간과 실질적 [[물리학적 공간]]을 나누어진다.<ref name = "네이버사전"></ref> | ||
| + | |||
| + | ===전공간적 위상=== | ||
| + | 지각에는 감각이 휠례적 계기로서 포함된 것처럼 [[전공간적]] 영역은 구체적 공간에 대해 생기가 불어넣어지고 통각이 되기 이전의 내재적 영역이다. 이것은 [[감각장]](시각장, 청각장, 촉각장)과 [[기관 운동장]](안구 운동장, 촉각 운동장)으로 나누어진다. 감각장은 중심을 지닌 원 형상의 불명확하게 경계 지어지는 2차원 연속체이며 중심과 주변이라는 위치 체계가 보이고 변화가 있지만, 어떠한 운동도 존재하지 않는다. 기관 운동장은 '나는 움직인다'라는 의식의 근거를 형성하는 운동 감각적 소여에 기초하는 것으로서 자세나 운동의 빠르기 또는 가속의 감각, 긴장감 나아가서 이들에 수반되는 고통감 등이 여기에 속한다. | ||
| + | |||
| + | 예를 들어 감각장의 어떤 형태의 변화가 형태 자신의 변화인가 아니면 나에 대한 위치의 이동에 의한 변화인가 하는 것은 '내가 움직인다'에 의해 그 변화가 본래대로 되돌려지는가 아닌가에 의해서 결정된다. 이를 통해 감각적인 합동 이동과 기관 운동적인 운동이 구별되고 중심, 주변이라는 위치에 체계가 임의로 움직여질 수 있게 되면 눈은 그 육체성을 제거당해 시광전행의 비물체적 기관이 되고 기관 운동장은 시광운동장이 된다. 신체 구성의 중요한 계기인 [[이중감각]]은 이러한 영역의 특이 현상이다.<ref name = "네이버사전"></ref> | ||
| + | |||
| + | ===구체적 공간=== | ||
| + | 이 공간은 체험된 공간 또는 생활 공간이라고도 불리지만, 그에 대한 해명은 후설의 지각이론과 하이데거의 현 존재의 공간성에 대한 분석 및 메를로, 퐁티의 신체론을 정초적인 업적을 하여 진전되어 왔다. 이 공간은 인간의 [[지정의]]라는 존재 방식에 대응하여 [[표상적]], [[상모적]], [[행동적]]인 세 가지 국면을 지니고 이 세 가지가 통합된 것이지만 그때마다 두드러진 국면을 따라서 직관적(표상적) 공간, 상모적(기분 지어진) 공간, 행동(행위) 공간으로 나누어질 수 있다. 행동 공간에서는 상하, 좌우, 전후라는 방향성이 두드러져 보이지만 그것은 신체의 기능성에 의한 바가 크다. 상모적 공간에선 이러한 방향성이나 [[표상 공간]]에서의 퍼스펙티브라는 것이 보이지 않고 등방도 이방도 아니면 무방(無方)이고 분위기적이다. 종교적 내지는 축제적인 성스러운 공간이나 예술적 공간은 다분히 상모적 공간에 따른다. 표상적 공간에서는 신체가 놓여 있는 여기를 원점으로 하는 깊이와 퍼스펙티브가 주목되는 현상이지만, 다른 공간과는 달리 이 공간은 미세하게 구조화되어있고 공간의 장소도 점적인 것으로까지 줄어들 수 있다. 더 나아가 시점(視點)과 장소의 이동에 의해서 신체라는 표상 공간 내의 중심점이 탈중심화되어 상호주관적인 [[공동공간]]이 구상되며 이념화에 의해 극한의 형태가 선취되어 이념적 공간이 성립된다.<ref name = "네이버사전"></ref> | ||
| + | |||
| + | ==형식적, 수학적 공간== | ||
| + | 예를 들어 곡면상에서 직선을 그을 수 있는가(원주면이나 원추면 등) 없는가(구면이나 의구면 등)와 같은 위상적인 성질과 [[전곡률]]이라고 불리는 공간의 일그러짐 정도는 그 곡률이 일정한지 아닌지 하는 계량 관계에 의해 분류된다([[유클리드 공간]], [[타원 공간]]). 그때 공간론의 전개는 몇 가지 수학적 절차에 기초한다. 기호를 매개로 한 형식화의 조작에 의해 수행되는 것(기하학의 대수화), 곡률의 판정이 근방이라는 극미의 범위에서 성립하는 것(미분기하학) 등이 이것들이다. 즉 수학적 공간은 이념화와 형식화의 조작에 의해 구성되지만 그러한 조작에는 수학적 귀납법에서 나오는 회귀적(반복 가능성의) 법칙성에 의한 무한의 과정의 선취라는 것이 따라다닌다. 예를 들어 이념적 존재인 수학적인 점은 구성이 완결되지 않는 한에서 구성 가능한 형성체라는 역설적인 의미가 있다.<ref name = "네이버사전"></ref> | ||
| + | |||
| + | ==실질적, 물리학적 공간== | ||
| + | [[표상 공간]]의 이념화에 의해 얻어지는 공간은 [[유클리드 공간]]이지만 이것은 실질적 공간(유클리드 기하학에서의 공간)이어서 수학에서 형식화된 유클리드 공간과는 구별된다. 이에 대해 고전 물리학에서 공간은 공간을 채우는 질(질량, 강체, 온도 등)이 그것에 짜 넣어진다는 것과 질의 규정이 인과성을 기초로 한다는 것(예를 들어 체적/온도 = 일정에 의한 온도의 규정)에 놓여있다. 결국 고전 물리학에서의 공간은 물질적, 인과적 사물과 유클리드 공간이 종합된 데서 성립한다. 그때 사물의 길이가 장소와 이동에 의해 변하지 않는다(기하하적으로 합동 변환이 성립한다는 것)고 하는 것에서 전형적으로 보이듯이 공간과 사물은 상호작용이 없는 것, 독립된 것으로 여겼다. 현대 물리학에서 공간은 시간과 일체화된 4차원 시공으로서 통합되고 고전 물리학에서의 자연의 인과성에 대해 의문이 들며 물질로부터의 공간 독립성이 포기되었지만, 시공적인 장과 물질이 어떻게 관계 지어지는지에 관한 물음은 해결되지 않고 있다.<ref name = "네이버사전"></ref> | ||
| + | |||
| + | ==물리학에서의 공간== | ||
| + | 물리학에서 공간의 정의는 여러 이론이 있다. 다음과 같이 다양한 개념으로 공간의 정의를 시도한다. | ||
| + | {{테두리색|#fff0f5|*물체 사이의 공간적 관계의 집합으로써 정의되는 구조 | ||
| + | |||
| + | *물체가 있는 좌표계에 의해 정의되는 [[다양체]] | ||
| + | |||
| + | *한 물체를 다른 물체와 분리되어 존재하게 하는 것 | ||
| + | }} | ||
| + | 고전 물리학에서 공간은 어느 한 위치가 3개의 좌표축에 의해서 기술되는 3차원 유클리드 공간이다. 상대론적 물리학에서는 공간보다 시공간을 더 고찰한다. 시공간은 4차원의 다양체로 모형화 되었으며, 요즘에는 그 이론이 11차원까지 여겨지고 있다. | ||
| + | |||
| + | 아인슈타인의 상대론적인 물리학 연구 이전에는 시간과 공간은 서로 독립적인 차원이라고 여겼으며 아인슈타인의 연구는 시간과 공간을 하나의 시공간을 통합했다. 시공간에서 시간과 공간의 측정은 속도에 상대적이다.<ref name = "위키"></ref> | ||
| + | |||
| + | ===공간의 차원=== | ||
| + | :{|class=wikitable width=600 style="background-color:#fff0f5" | ||
| + | |+차원(Dimension) | ||
| + | !align=center style="background-color:#FFB6C1"|구분 | ||
| + | !align=center style="background-color:#FFB6C1"|[[0차원]] | ||
| + | !align=center style="background-color:#FFB6C1"|[[1차원]] | ||
| + | !align=center style="background-color:#FFB6C1"|[[2차원]] | ||
| + | !align=center style="background-color:#FFB6C1"|[[3차원]] | ||
| + | !align=center style="background-color:#FFB6C1"|n차원 | ||
| + | |- | ||
| + | !align=center style="background-color:#FFB6C1"|위상 | ||
| + | |align=center|점 | ||
| + | |align=center|선 | ||
| + | |align=center|면 | ||
| + | |align=center|입체 | ||
| + | |align=center|초입체 | ||
| + | |- | ||
| + | !align=center style="background-color:#FFB6C1"|측도 | ||
| + | |align=center|셈 측도 | ||
| + | |align=center|길이 | ||
| + | |align=center|넓이 | ||
| + | |align=center|부피 | ||
| + | |align=center|초부피 | ||
| + | |- | ||
| + | |align=center colspan=2|[[유클리드 공간]] | ||
| + | |align=center colspan=2|[[민코프스키 시공간]] | ||
| + | |align=center colspan=2|[[측도론]] | ||
| + | |} | ||
| + | 공간의 차원은 생물학을 비롯하여 물리법칙에 큰 영향을 끼친다. 2차원 이하의 생명체는 지능을 가질 수 없다고 여기고 3차원에선 뉴런이 임의의 수의 뉴런과 연결될 수 있지만, 2차원에서는 신경이 교차할 수 없음으로 이것은 불가능하다. | ||
| + | |||
| + | [[가우스 법칙]]에 따라 2차원 이하에서는 거리가 커질 때 [[퍼텐셜]] 발산하고 이로 인해 행성의 궤도는 언제나 속박되어 있으며 원자의 이온화도 불가능하다. 3차원에서는 유효퍼텐셜이 아래로 볼록하여 근일점과 원일점 사이를 오가는 안정한 궤도가 가능하다. 4차원에서 천체는 원 궤도만 가능하고 타원 궤도는 불가능하다. 5차원 이상은 유효퍼텐셜이 위로 볼록하여 천체는 궤도를 이루지 못한다. | ||
| + | |||
| + | 디랙 방정식을 고려하였을 때, 4차원 이상에서는 안정한 수소 원자 모형이 존재하지 않는다. | ||
| + | |||
| + | 짝수 차원에서는 파동이 0~c의 다양한 속도로 전파되어 다른 시간에 생긴 파동이 동시에 도달하는 문제가 발생한다. 홀수 중에서도 1, 3차원에서만 파동이 파원의 진폭에 정확히 비례하는 방식으로 전달된다.<ref name = "나무"></ref> | ||
| + | |||
| + | ==천문학에서의 공간== | ||
| + | [[천문학]]에서 공간은 [[우주]]의 빈 부분을 통합하여 이야기한다. 천체의 대기권 바깥 부분을 공간이라고 말할 수 있다. 우주 공간과 지구의 대기권 사이의 경계는 통상적으로 [[카르만]] 선에서 정해진다.<ref name = "위키"></ref> | ||
| + | |||
| + | ==수학에서의 공간== | ||
| + | 수학에서 공간은 몇 가지의 특별한 속성과 부가적 구조를 가지는 집합이다. 가끔 공간은 벡터 공간 또는 자기 자신의 특이한 변형이다.<ref name = "위키"></ref> | ||
| + | ===바나흐 공간=== | ||
| + | 함수 해석학에서 바나흐 공간(空間, Banach space)은 완비 노름 공간이다. 스테판 바나흐의 이름을 따왔다. | ||
| + | ;정의 | ||
| + | <math>\mathbb K\in\{\mathbb R,\mathbb C\}</math>가 [[실수체]] 혹은 [[복소수체]]라고 한다. | ||
| + | |||
| + | <math>\mathbb K</math>-노름 공간 <math>(X,\|\cdot\|)</math>에 대하여 다음 두 조건이 서로 동치이고, 이것을 만족시키는 <math>\mathbb K</math>-노름 공간을 <math>\mathbb K</math>-바나흐 공간이라고 한다. | ||
| + | * [[노름]]으로 정의한 [[거리 함수]]를 부여하게 되면, [[완비 거리 공간]]이다. 모든 코시 열이 수렴한다. | ||
| + | * 모든 절대 수렴 급수가 수렴한다. 임의의 점렬 <math>(v_i)_{i\in\mathbb N}\subseteq X</math>에 대하여, 만약 <math>\textstyle\sum_{i\in\mathbb N}\|v_i\|<\infty</math>라면, 급수 <math>\textstyle\sum_{i\in\mathbb N}v_i</math> 역시 노름으로 정의한 [[거리 위상]]에 대해 수렴한다. | ||
| + | 체 <math>\mathbb K</math>를 실수체 혹은 복소수체로 국한하는 이유는 노름 공간에 완비성을 가정하려면 그 체가 완비되어야 하기 때문이다. 예를 들어서 [[유리수체]]는 완비되지 못한다.<ref>〈[https://ko.wikipedia.org/wiki/%EB%B0%94%EB%82%98%ED%9D%90_%EA%B3%B5%EA%B0%84 바나흐 공간]〉, 《위키백과》</ref> | ||
| + | |||
| + | ===유클리드 공간=== | ||
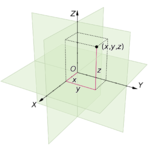
| + | [[파일:유클리드 공간.png|썸네일|150픽셀|3차원 유클리드 공간상의 각 점은 3개의 좌표축에 의해 결정된다.]] | ||
| + | 수학에서 유클리드 공간(Euclidean space)은 유클리드가 연구했던 평면과 공간을 일반화한 것이다. 일반화는 유클리드가 생각했던 거리와 길이와 각도를 좌표계에 도입하여 임의 차원의 공간으로 확장한 것이다. 이것은 표준적인 유한 차원, 실수, 내적 공간이다. 때에 따라 [[민코프스프키]] 공간에 대비되는 주장으로 [[피타고라스의 정리]]에 의한 길이 소의 제곱 계수가 모두 양수인 공간을 말한다. | ||
| + | ;정의 | ||
| + | 음이 아닌 정수 <math>n=0,1,2,\dots</math>에 대해 <math>n</math>차원 유클리드 공간 <math>\mathbb R^n</math>은 집합으로서 실수 집합 <math>\mathbb R</math>의 <math>n</math>번 [[곱집합]]이다. | ||
| + | |||
| + | 이 위에 내적 | ||
| + | :<math>\langle u,v\rangle=\sum_{i=1}^nu_iv_i</math> 를 정의하면, | ||
| + | <math>\mathbb R^n</math>은 실수 [[힐베르트 공간]]을 이룬다. 이에 따라서 유클리드 공간은 [[내적 공간]], [[바나흐 공간]], [[노름 공간]], [[벡터 공간]], [[완비 거리 공간]], [[위상 공간]]을 이룬다. | ||
| + | |||
| + | 자명한 좌표근방계를 주어서 매끄러운 다양체 및 리만 다양체로 만들 수 있다. 이러한 겨우, 리만 계량으로 정의한 거리는 [[내적]]으로 정의한 거리와 일치하다.<ref>〈[https://ko.wikipedia.org/wiki/%EC%9C%A0%ED%81%B4%EB%A6%AC%EB%93%9C_%EA%B3%B5%EA%B0%84 유클리드 공간]〉, 《위키백과》</ref> | ||
| + | |||
| + | ===힐베르트 공간=== | ||
| + | 함수 해석학에서 [[힐베르트 공간]](Hilbert space)은 모든 [[코시 열]]의 극한이 존재하는 [[내적 공간]]이다. 유클리드 공간을 일반화한 개념이다. | ||
| + | ;정의 | ||
| + | <math>K</math>가 <math>\mathbb R</math> 또는 <math>\mathbb C</math>라고 할 때, <math>K</math>-힐베르트 공간 <math>(\mathcal H,\langle\cdot,\cdot\rangle)</math>은 완비 거리 공간을 이루는 <math>K</math>-내적 공간이다. 내적 공간인 힐베르트 공간은 표준적인 위상 공간, 거리 공간, 벡터 공간, 노름 공간 중에서 원하는 구조를 갖는다. | ||
| + | |||
| + | 이와 논리가 같은 것으로, <math>K</math>-힐베르트 공간을 다음과 같은 평행사변형 항등식을 만족시키는 <math>K</math>-바나흐 공간 <math>(\mathcal H,\|\cdot\|)</math>으로 정의할 수 있다. | ||
| + | :<math>\|u+v\|^2+\|u-v\|^2=2(\|u\|^2+\|v\|^2)\qquad\forall u,v\in\mathcal H</math> | ||
| + | 이러한 경우 내적 구조는 | ||
| + | :<math>\langle u,v\rangle=\begin{cases} | ||
| + | \frac14\left(\|u+v\|^2-\|u-v\|^2\right)&K=\mathbb R\\ | ||
| + | \frac14\left(\|u+v\|^2-\|u-v\|^2+i\|u+iv\|^2-i\|u-iv\|^2\right)&K=\mathbb C\\ | ||
| + | \end{cases}</math> 가 된다. | ||
| + | |||
| + | ===거리 공간=== | ||
| + | 수학에서 [[거리 공간]](metric space)은 두 점 사이의 거리가 정의된 공간이다. 거리의 정의에 따라 표준적인 위상을 가진다. | ||
| + | ;정의 | ||
| + | 집합 <math>X</math> 위의 거리 함수는 다음 조건을 만족시키는 함수 <math>d\colon X \times X \to[0,\infty)</math> 이다. | ||
| + | * 구분 불가능한 점의 동일성인 임의의 <math>x,y\in X</math>에 대해서 <math>d(x,y) = 0 \iff x = y </math> | ||
| + | * 대칭성인 임의의 <math>x,y\in X</math>에 대해서 <math>d(x,y) = d(y,x)</math> | ||
| + | * 삼각 부등식인 임의의 <math>x,y,z\in X</math>에 대해서 <math>d(x,y) + d(y,z) \ge d(x,z)</math> | ||
| + | 마지막 두 [[공리]]는 다음과 같은 하나의 공리로 바꿀 수 있다. | ||
| + | * [[삼각 부등식]]인 <math>d(z,y) + d(y,x) \ge d(x,z)</math> | ||
| + | 여기서 <math>y=x</math>로 설정하면, <math>d(y,x)=d(x,y)</math>가 되어, 대칭 공리를 얻는다. [[거리 함수]]의 정의에서, 첫째 조건을 <math>d(x,y)=0\Longleftarrow x=y</math>로 약화시키게 되면 [[유사 거리 함수]]의 개념을 얻는다. | ||
| + | 거리 공간 <math>(X,d)</math>은 거리 함수가 주어진 집합이다.<ref>〈[https://ko.wikipedia.org/wiki/%EA%B1%B0%EB%A6%AC_%EA%B3%B5%EA%B0%84 거리 공간]〉, 《위키백과》</ref> | ||
| + | |||
| + | ===벡터 공간=== | ||
| + | 선형대수학에서 [[벡터 공간]](vector space) 또는 [[선형 공간]](linear space)은 원소를 서로 더하거나 주어진 배수로 늘이거나 줄일 수 있는 공간이다. [[체]]에 대한, [[가군]]의 특수한 경우이다. 벡터 공간의 원소를 벡터라고 하고 이것은 직관적으로 방향 및 길이의 비가 정의된 대상을 나타낸다. 그러나 노름이 주어지지 않은 일반적인 벡터 공간에서는 벡터의 길이 자체는 정의되지 않는다. | ||
| + | ;정의 | ||
| + | 체 <math>K</math> 위의 벡터 공간 <math>(V,+,\cdot)</math>은 <math>K</math>에 대한 가군 이다. 다음과 같은 [[튜플]]이다. | ||
| + | * <math>V</math>는 집합이고 이 집합의 원소를 벡터라고 한다. | ||
| + | * <math>+\colon V\times V\to V</math>는 함수이고 이 연산을 [[벡터 덧셈]]이라고 한다. | ||
| + | * <math>\cdot\colon K\times V\to V</math>는 함수이고 이 연산을 [[스칼라 곱셈]]이라고 한다. | ||
| + | 이와 같은 데이터는 다음과 같은 공리들을 만족시켜야 한다. | ||
| + | * <math>(V,+)</math>는 아벨 군을 이루고 다음과 같은 성질들이 성립한다. | ||
| + | ** 벡터 덧셈의 [[결합 법칙]]인 임의의 <math>u,v,w\in V</math>에 대해서 <math>(u+v)+w=u+(v+w)</math> | ||
| + | ** 벡터 덧셈의 [[교환 법칙]]인 임의의 <math>u,v\in V</math>에 대해서 <math>u+v=v+u</math> | ||
| + | ** 벡터 덧셈의 [[항등원]]인 임의의 <math>u\in V</math>에 대해서 <math>u+0=u</math>인 [[원소]] <math>0\in V</math>가 존재한다. | ||
| + | ** [[역원]]의 존재인 임의의 <math>u\in V</math>에 대해서 <math>-u+u=0</math>인 원소 <math>-u\in V</math>가 존재한다. | ||
| + | * <math>(V,+,\cdot)</math>는 <math>K</math>의 가군을 이루고 다음과 같은 성질들이 성립한다. | ||
| + | ** 임의의 <math>a,b\in K</math> 및 <math>v\in V</math>에 대해서 <math>a\cdot(b\cdot v)=(ab)\cdot v</math> | ||
| + | ** 임의의 <math>v\in V</math>에 대해서 <math>1\cdot v=v</math>. 여기서 <math>1\in K</math>는 <math>K</math>의 곱셈 항등원이다. | ||
| + | ** 분배 법칙인 임의의 <math>a,b\in K</math> 및 <math>u,v\in V</math>에 대해서 <math>(a+b)\cdot(u+v)=a\cdot u+b\cdot u+a\cdot v+b\cdot v</math> | ||
| + | |||
| + | [[실수체]] <math>\mathbb R</math>에 대한 벡터 공간을 [[실수 벡터 공간]](real vector space)이라 칭하고 [[복소수체]] <math>\mathbb C</math>에 대한 벡터 공간을 [[복소수 벡터 공간]](complex vector space)이라고 칭한다.<ref>〈[https://ko.wikipedia.org/wiki/%EB%B2%A1%ED%84%B0_%EA%B3%B5%EA%B0%84 벡터 공간]〉, 《위키백과》</ref> | ||
| + | |||
| + | ===사영 공간=== | ||
| + | 수학에서 사영 공간(projective space, 射影空間)은 벡터 공간의 원점을 지나는 직선들의 집합이다. 평행선들이 만나는 장소인 무한 원 직선이나 무한 원 평면 등의 개념을 다루기 위해서 만들어진 개념이다. 사영 공간의 기하학을 다루는 학문인 사영기하학은 현대 대수기하학의 기초가 되었고 사영 공간 및 이를 확장한 개념인 그라스만 다양체와 깃발 다양체는 위상 수학, 리 군론, 대수 군로 및 이 대상들의 표현론에서 중요한 역할을 맡는다. | ||
| + | ;정의 | ||
| + | 음이 아닌 정수 <math>n\in\mathbb N</math>이 주어졌다고 가정했을 때, | ||
| + | 정수 계수의 <math>n</math>차원 사영 공간 <math>\mathbb P^n_{\mathbb Z}</math>은 다음과 같다. | ||
| + | :<math>\mathbb P^n_{\mathbb Z}=\operatorname{Proj}\mathbb Z[x_0,x_1,\dots,x_n]</math> | ||
| + | 여기서 <math>\mathbb Z[x_0,x_1,\dots,x_n]</math>은 [[등급환]]인 정수 계수 [[다항식환]]이며, <math>\operatorname{Proj}</math>는 [[사영 스펙트럼]]이다. | ||
| + | |||
| + | 임의의 [[스킴]] <math>X</math>에 대해서 <math>X</math> 좌표의 <math>n</math>차원 사영 공간 <math>\mathbb P_X^n</math>은 다음과 같다. | ||
| + | :<math>\mathbb P^n_X=\mathbb P^n_{\mathbb Z}\times X</math> | ||
| + | 여기서 <math>\times</math>는 스킴의 범주의 곱을 뜻한다. | ||
| + | |||
| + | 만약 <math>R</math>가 [[가환환]]이라면 다음이 성립한다. | ||
| + | :<math>\mathbb P^n_{\operatorname{Spec}R} = \operatorname{Proj}R[x_0,x_1,\dotsc,x_n]</math> | ||
| + | |||
| + | <math>K</math>가 대수적으로 닫힌 체라고 했을 때, <math>\mathbb P^n_K</math>의 닫힌 점들은 다음과 같이 구체적으로 정의할 수 있다. <math>K^{n+1}\setminus\{(0,0,\dots,0)\}</math>에 다음과 같은 [[동치 관계]]를 준다. | ||
| + | :<math>(a_0,a_1,\dots,a_n)\sim(\lambda a_0,\lambda a_1,\dots,\lambda a_n)\qquad\forall\lambda\in K^\times</math> | ||
| + | 그렇다면 <math>\mathbb P^n_K</math>의 닫힌 점들은 동치류 집합 <math>(K^{n+1}\setminus\{(0,0,\dots,0)\})/{\sim}</math>에 대응한다. 이러한 경우, <math>(a_0,\dots,a_n)</math>을 [[동차좌표]]라고 한다.<ref>〈[https://ko.wikipedia.org/wiki/%EC%82%AC%EC%98%81_%EA%B3%B5%EA%B0%84 사영 공간]〉, 《위키백과》</ref> | ||
| + | |||
| + | ===위상 공간=== | ||
| + | 일반 위상 수학에서 위상 공간(topological space, 位相空間)은 어떤 점의 근방이 무엇인지에 대한 정보를 담고 있지만, 점 사이의 거리, 부피, 넓이의 정보를 포함하지 않는 공간이다. 이것을 사용하여 함수의 연속성이나 수열의 극한, 집합의 연결성 등을 정의할 수 있다. 위상 공간의 개념은 위상 수학 및 이를 기초로 하는 기하학, 해석학에서 핵심적으로 사용된다. 위상 공간의 일반적인 성질을 연구하는 분야가 일반 위상 수학이다. | ||
| + | ;정의 | ||
| + | [[집합]] <math>X</math> 위의 위상은 다음과 같이 여러가지로 정의할 수 있다. | ||
| + | *열린집합을 사용한 정의: 다음 조건을 만족 시키는 [[부분 집합]]들의 모임 <math>\mathcal T\subseteq\mathcal P(X)</math>. 이러한 경우 <math>\mathcal T</math>의 원소들을 [[열린집합]]이라고 한다. | ||
| + | ** <math>\varnothing,X\in\mathcal T</math> | ||
| + | ** 만약 <math>\mathcal S\subseteq\mathcal T</math>라면, <math>\bigcup\mathcal S\in\mathcal T</math> | ||
| + | ** 만약 <math>U,V\in\mathcal T</math>라면, <math>U\cap V\in\mathcal T</math> | ||
| + | * 닫힌집합을 사용한 정의: 다음 조건을 만족 시키는 부분 집합들의 모임 <math>\mathcal C\subseteq\mathcal P(X)</math>. 이러한 경우 <math>\mathcal C</math>의 원소들을 [[닫힌집합]]이라고 한다. | ||
| + | **<math>\varnothing,X\in\mathcal C</math> | ||
| + | ** 만약 <math>\mathcal S\subseteq\mathcal C</math>라면, <math>\bigcap\mathcal S\in\mathcal C</math> | ||
| + | ** 만약 <math>C,D\in\mathcal C</math>라면, <math>C\cup D\in\mathcal C</math> | ||
| + | * 근방을 사용한 정의: 다음 조건을 만족 시키는 함수 <math>\mathcal N\colon X\to\mathcal P(\mathcal P(X))</math>. 이러한 경우 <math>\mathcal N\colon x\mapsto\mathcal N_x</math>로 쓰고, <math>\mathcal N_x</math>의 원소를 <math>x</math>의 [[근방]]이라 한다. | ||
| + | ** 모든 <math>x\in X</math>에 대해서, <math>X\in\mathcal N_x</math> | ||
| + | ** 모든 <math>x\in X</math>에 대해서, 만약 <math>N\in\mathcal N_x</math>라면 <math>x\in N</math> | ||
| + | ** 만약 <math>N\in\mathcal N_x</math>이며 <math>N\subseteq S\subseteq X</math>라면, <math>S\in\mathcal N_x</math> | ||
| + | ** 만약 <math>M,N\in\mathcal N_x</math>라면 <math>M\cap N\in\mathcal N_x</math> | ||
| + | ** 만약 <math>N\in\mathcal N_x</math>라면, <math>N\in\mathcal N_y\qquad\forall y\in M</math>인 <math>M\in\mathcal N_x</math>가 존재한다. | ||
| + | * 폐포를 사용한 정의: 다음 조건을 만족 시키는 함수 <math>\operatorname{cl}\colon\mathcal P(X)\to\mathcal P(X)</math>. 이러한 경우 <math>\operatorname{cl}S</math>를 <math>S</math>의 [[폐포 ]]라고 한다. | ||
| + | ** <math>\operatorname{cl}\varnothing = \varnothing</math> | ||
| + | ** 모든 <math>A\subseteq X</math>에 대해서 <math>A\subseteq\operatorname{cl} A</math> | ||
| + | ** 모든 <math>A,B\subseteq X</math>에 대해서 <math>\operatorname{cl}(A \cup B) = \operatorname{cl}(A) \cup \operatorname{cl}(B)</math> | ||
| + | ** 모든 <math>A\subseteq X</math>에 대해서 <math>\operatorname{cl}(\operatorname{cl}A) = \operatorname{cl}A</math> | ||
| + | * 내부를 사용한 정의: 다음 조건을 만족 시키는 함수 <math>\operatorname{int}\colon\mathcal P(X)\to\mathcal P(X)</math>. 이러한 경우 <math>\operatorname{int}S</math>를 <math>S</math>의 내부라고 한다. | ||
| + | ** <math>\operatorname{int}X = X</math> | ||
| + | ** 모든 <math>A\subseteq X</math>에 대해서 <math>A\supseteq\operatorname{int}A</math> | ||
| + | ** 모든 <math>A,B\subseteq X</math>에 대해서, <math>\operatorname{int}(A \cap B) = \operatorname{int}(A) \cap \operatorname{int}(B)</math> | ||
| + | ** 모든 <math>A\subseteq X</math>에 대해서 <math>\operatorname{int}(\operatorname{int}A) = \operatorname{int}A</math> | ||
| + | 이 정의들은 서로 [[동치]]이다. | ||
| + | * 열린집합을 사용한 정의에서, | ||
| + | ** [[닫힌집합]]은 [[열린집합]]의 여집합이다. | ||
| + | ** <math>x</math>의 근방의 모임은 <math>\mathcal N_x=\{S\subset X\colon\exists U\in\mathcal T\colon x\in U\subseteq S\}</math>이다. | ||
| + | ** 집합 <math>S</math>의 폐포는 <math>\operatorname{cl}S=\bigcap\{X\setminus U\colon U\in\mathcal T,\;U\cap S=\varnothing\}</math>이다. | ||
| + | ** 집합 <math>S</math>의 내부는 <math>\operatorname{int}S=\bigcup\{U\in\mathcal T\colon U\subseteq S\}</math>이다. | ||
| + | * 닫힌집합을 사용한 정의에서, 열린집합은 닫힌집합의 여집합이다. | ||
| + | * 근방을 사용한 정의에서, 열린집합은 <math>\forall x\in U\colon U\in\mathcal N_x</math> 인 집합 <math>U</math>이다. | ||
| + | * 폐포를 사용한 정의에서, 열린집합은 <math>\operatorname{cl}(X\setminus U)=X\setminus U</math>인 집합 <math>U</math>이다. | ||
| + | * 내부를 사용한 정의에서, 열린집합은 <math>\operatorname{int}(U)=U</math>인 집합 <math>U</math>이다. | ||
| + | 결과적으로 [[근방]] · [[열린집합]] · [[닫힌집합]] · [[폐포]] · [[내부]] 가운데 하나를 기본 무정의 개념으로 삼고, 이로부터 나머지 개념들을 정의할 수 있다. | ||
| + | |||
| + | 위상 공간<math>(X,\mathcal T)</math>은 위상을 갖춘 집합이다.<ref>〈[https://ko.wikipedia.org/wiki/%EC%9C%84%EC%83%81_%EA%B3%B5%EA%B0%84_(%EC%88%98%ED%95%99) 위상 공간]〉, 《위키백과》</ref> | ||
| + | |||
| + | ===확률 공간=== | ||
| + | 확률론에서 확률 공간(probability space, 確率空間)은 천체 측도가 1인 측도 공간이다. 확률적인 현상에서 확률 공간의 측도는 확률을 정의 한다. | ||
| + | ;정의 | ||
| + | 확률 공간 <math>(\Omega,\mathcal F,\Pr)</math>은 공간 전체의 [[측도]]가 1인 [[측도 공간]]이다. | ||
| + | :<math>\Pr(\Omega)=1</math> | ||
| + | [[확률론]]에서는 [[측도론]]의 용어와 다른 각종 용어들이 이용된다. | ||
| + | * 확률 공간의 점들의 집합 <math>\Omega</math>는 [[표본 공간]]이라 한다. | ||
| + | * 확률 공간의 [[가측 집합]] <math>S\in\mathcal F</math>은 사건(llang|en|event)이라 한다. | ||
| + | * 사건 <math>S\in\mathcal F</math>의 측도 <math>\Pr(S)</math>는 사건의 확률이라 한다. | ||
| + | 확률론의 용어를 사용하게 되면 측도 공간의 각종 성질은 다음과 같다. | ||
| + | * 사건 <math>S\subset\Omega</math>에 대해서 그 여집합 <math>\Omega\setminus S</math> 역시 사건이다. 어떤 사건에 대하여, 그 사건이 일어나지 않는 경우 역시 사건이다. | ||
| + | * 가산 개의 사건들이 주어졌을 때, 그 합집합과 교집합 역시 사건이다. 사건들의 열이 주어졌을 때, 사건의 열 가운데 적어도 하나가 일어나는 경우(합집합)도 사건을 이루며, 사건의 열이 모두 일어나는 경우 (교집합) 또한 사건을 이룬다. | ||
| + | * [[공집합]]과 전체 집합은 사건이다. 불가능한 사건(공집합)과 필연적인 사건(전체 집합)이 존재한다.<ref>〈[https://ko.wikipedia.org/wiki/%ED%99%95%EB%A5%A0_%EA%B3%B5%EA%B0%84 확률 공간]〉, 《위키백과》</ref> | ||
| + | |||
| + | ==불교에서의 공간== | ||
| + | [[불교]]에서의 공간은 모든 유위, 무위법이 존재한다. 활동하는 장소인 [[무위법]]으로서의 절대 공간에 해당하는 [[허공]](虛空) 또는 [[허공 무위]](虛空無爲)와 [[유위법]]이면서 [[가법]]인 [[심불상응행법]]에 속한 방위와 방향, 공간으로서의 방(方)을 구분한다. 불교 일반에서는 시(時), 시간과 과거, 현재, 미래에 대해서는 실재하지 않는 법을 마치 실재법인 것처럼 삼은 것이라고 본다. 이것을 가법이라고 한다. | ||
| + | |||
| + | [[부파불교]]의 [[설일체유부]]에서는 절대 공간인 허공이 별개의 실체, [[실법]]이라 한다. 반면에 [[대승 불교]]에선 절대 공간인 허공을 [[진여]]의 한 측면이라고 보고, 진여라는 실법에 근거하여 가립한 가법이라고 한다. 하지만 절대 공간을 부파 불교에서와 마찬가지로 허공 무위라고 칭한다. 불교 일반에서는 마음(6식 또는 8식, [[심왕]], [[심법]])은 무위법이 아닌 유위법이라고 보며 마음을 온갖 [[심소법]](心所法)들, 즉 선(善) · 불선(不善) · 무기(無記)의 온갖 마음의 작용들이 일어나고[生] 작용하고[住] 사라지는[滅] 변화하고[異] 장소 또는 공간이라는 뜻에서 [[지]](地)라고도 칭한다.<ref name = "위키"></ref> | ||
| + | |||
| + | ==철학에서의 공간== | ||
| + | 시간과 공간의 철학으로는 아래와 같은 물음이 고찰되고 있다. | ||
| + | * [[시간]]이나 공간은 그중에 있는 물체와 독립에 실재하는가 아니면 어디까지나 물체의 관계로만 존재하는 것인가? | ||
| + | :→ 시간의 [[반실재론]]으로는 [[존 마크타가트]]가 유명하며, 공간의 관계설을 주장한 철학자로서 [[고트프리트 빌헬름 라이프니츠]]나 [[에른스트 마하]]가 알려져 있다. | ||
| + | |||
| + | * 만약 시공이 존재한다면, 그것은 실체를 가지는가? | ||
| + | :→ 아인슈타인의 [[일반 상대성 이론]]은 [[시공]]을 실체적으로 파악하는 것과 통상을 이해할 경우 [[실체설]](substantivism)에 서게 된다. 시공의 반실체설의 논자로는 존 아만등이 있다. | ||
| + | |||
| + | * 시공의 구조가 리만 기하학적이라는 것은 객관적인 사실인가? 그렇지 않으면 기술의 방법에 상대적 단순한 규칙인가? | ||
| + | :→ [[아이슈타인]]은 일반 상대성 이론의 시공이 리만 공간인 것을 객관적인 사실이라고 생각했지만, 이것을 단순한 규약이라고 생각한 철학자들도 많았다. 규약 주의를 주장한 철학자로서는 [[앙리 푸앵카레]], [[한스 라이헨바흐]] 등이 있다. | ||
| + | |||
| + | * 시간의 방향을 결정하는 것은 무엇인가(시간의 화살)? | ||
| + | :→ 기본적인 물리 법칙은 모두 시간 대칭이어서, 이들에 따라서 시간의 방향은 정의할 수 없다. [[열역학 제2 법칙]]을 이용해서 시간의 방향을 정의하는 생각, 우주의 팽창을 이용하여 시간의 방향을 정의하는 생각, [[양자 역학]]에서의 파속의 수습을 통해 시간의 방향을 정의하는 생각 등이 제안되어왔다. | ||
| + | |||
| + | * 역방향의 인과는 가능한 일인가, 시간 여행은 가능한가? | ||
| + | :→ 시간과 공간이 본질적으로 다르지 않은 것이 상대성 이론으로부터 나타났다. 광속을 넘어 이동하는 것으로 역방향 인과나 과거의 시간 여행도 할 수 있는 것이 아닌가 하는 가능성이 제기되었다. 하지만 시간 여행은 원리적을 불가능하다고 생각하는 논자도 있었다.<ref>〈[https://ko.wikipedia.org/wiki/%EC%8B%9C%EA%B0%84%EA%B3%BC_%EA%B3%B5%EA%B0%84%EC%9D%98_%EC%B2%A0%ED%95%99 시간과 공간의 철학]〉, 《위키백과》</ref> | ||
| + | |||
| + | ==마음에서의 공간== | ||
| + | 역사적으로 공간은 인간의 심적 작용이 일어나는 마음을 담고 있는 그릇과 같은 것으로 비유됐다. 이러한 의미에서 공간의 역할을 강조한 빈 공간은 [[문학]], [[심리학]], [[종교]], [[철학]] 등에서 마음을 적절히 표현하기 위해 다양하게 언급하거나 비유했다.<ref name = "위키"></ref> | ||
| + | |||
| + | ==가상 공간== | ||
| + | [[가상 공간]](假想 空間) 혹은 [[사이버 공간]] 또는 [[사이버스페이스]](cyberspace)는 현실 세계가 아닌 컴퓨터, 인터넷 등으로 만들어진 가상의 공간을 의미한다. | ||
| + | ;정의 | ||
| + | 사이버스페이스라는 용어는 [[윌리엄 깁슨]]이 1984년에 쓴 과학 소설인 [[뉴로맨서]]에서 최초로 등장했다. 인공 두뇌학(cybernetics)을 뜻하는 Cyber와 공간을 뜻하는 Space의 합성어로서 현실이 아닌 두뇌 속에서 펼쳐지는 또 다른 우주를 뜻한다. 사이버스페이스라는 용어는 [[존 페리 발로]]가 의사 전달의 공간(Communication Space)이라는 개념으로 사용하면서부터 일상적인 용어가 됐다. | ||
| + | |||
| + | 사이버스페이스에선 국경과 이념의 한계가 없고 지리적 위치, 시간, 신분상의 제한을 받지 않고 누구에게나 실시간 혹은 비실시간으로 정보의 선택 및 송수인 가능하다. 사이버스페이스에선 다양한 활동을 할 수 있는데, 사이버 교육은 이러한 사이버 공간 내에서 이루어지는 교육의 한 사례이다. [[컴퓨터]], [[인터넷]]상의 [[데이터]] 영역을 다수의 이용자가 자유롭게 정보를 주고받는 곳이고 최근에는 컴퓨터 네트워크상에서 행해지는 범죄를 사이버 범죄라고 칭한다. 컴퓨터 [[네트워크]]상에 구성된 사회, 즉 사이버스페이스에 대한 인식이 정착되었다.<ref>〈[https://ko.wikipedia.org/wiki/%EA%B0%80%EC%83%81_%EA%B3%B5%EA%B0%84 가상 공간]〉, 《위키백과》</ref> | ||
| + | |||
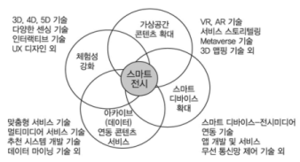
| + | ==스마트공간== | ||
| + | [[메타버스]](metaverse) 개념을 [[전시공간]] 구축에 활용한다는 것은 매우 흥미롭고 의미 있는 일이다. 메타버스에는 물리적 전시공간에 담긴 모든 콘텐츠를 담아낼 수 있다. 물리적 공간의 한계를 넘어서 제한 없이 콘텐츠를 담아낼 수 있을뿐더라 콘텐츠의 형태와 구성 방식도 전시 목적에 따라서 얼마든지 자유롭게 구축할 수 있다. 물리적 전시공간 내 매체 시스템의 작동에 의해서 원하는 사용자에게 콘텐츠로 제공된다. 메타버스 개념의 활용은 전시공간을 풍성하고 스마트하게 하는 것에 도움을 준다.<ref name = "메타">김성희·이현우·류원·김광신, 〈[https://www.koreascience.or.kr/article/JAKO201452057196673.pdf 스마트공간과 메타버스 전시안내 기술개발 동향]〉, 《전자통신동향분석 제29권 제3호》, 2014-06</ref> | ||
| + | |||
| + | 인간들은 특정 목적으로 [[공간]]을 구획하고 창출하거나 파기하여 공간 내에서 사회생활을 이어간다. 인간의 모든 사회생활이 다양한 공간 속에서 다뤄지며 사회생활의 다양한 단위들이 공간을 통해 특징적으로 개념 지어지기도 한다. 사회생활의 많은 부분이 공간을 매개로 이루어지고 있다. 공간 개념은 세계, 대륙, 영토, 지역, 국가 등 상대적으로 추상성 높은 공간과 주택, 방, 극장처럼 물리적 특성이 구체적인 공간을 모두 포함한다. 전시공간은 근대 이후 성립된 종합 박물관(Museum)과 근대 이후 분화 발전해 온 미술관(Museum of Art), 과학관(Museum of Science) 등의 특화 박물관, 세계박람회(EXPO)와 여기서 분화된 테마파크, 전시 컨벤션 등을 포괄한다. 사람들은 정보 획득, 학습, 오락 등을 목적으로 전시공간을 방문하여 관람하고 체험하는 공간적 실천을 하고 있다. 전시공간은 전시를 주관하는 주체의 공간적 실천을 통해 생성되며, 대중들의 다양한 목적의 공간적 실천을 통해 활용되는 두 가지 공간적 실천이 중첩되는 [[문화]]영역이다.<ref name = "메타"></ref> | ||
| + | |||
| + | ===유비쿼터스 환경=== | ||
| + | 전시공간을 포함한 [[문화공간]]을 [[제3의 공간]]으로 분류하는 기준이 있다. 인간이 만든 사회적 공간 중 제1의 공간(the first space)을 주거공간으로 [[제2의 공간]](thesecond space)을 일하는 공간으로 했다. 1980년대 들어 [[제1의 공간]]도 아니고 제2의 공간도 아닌데 감각적으로 짜릿하고 집처럼 편안한 문화공간에 대한 대중들의 수요가 발생하면서 조성되는 이러한 문화공간을 제3의 공간(the third space)으로 분류했다. 제4의 공간(4D space)이란 개념의 논의도 있다. 공간의 진화 방향을 예측한 [[제4의 공간]]은 [[디지털 기술]]의 발달 이후 인간의 행동에 반응하는 공간(responsiveenvironments)에 대한 새로운 개념이다. | ||
| + | |||
| + | 조성되는 건축에 마치 하나의 구조물처럼 [[인터랙티브 디지털 매체]]가 설치되어 있음으로 인간의 행동에 반응하는 공간이 생성된다. 이러한 공간환경은 전시공간 구축에서 최근 많이 활용되고 있다. 이러한 공간은 특히 [[첨단기술]]을 활용하는 [[세계박람회]]의 전시공간에서 많이 활용된다. 공간에서 인간 행동이나 인터랙티브 작동행위를 감지하고, 이에 따라 공간의 분위기가 달라지거나, 특정 퍼포먼스가 일어나거나, 특정 정보가 제공되는 등의 반응이 일어나는 시스템이다. [[미디어 월]](mediawall), [[인터랙티브 플로어]](interactive floor), [[미디어 테이블]](media table) 등의 개념이 인터랙티브 공간을 형성하는 매체들이고 그 밖에도 다양한 [[센싱 기술]]과 [[유무선 네트워크 기술]]을 [[디지털 전시 매체]]와 조합하고 시스템화하면 다양한 인터랙티브 콘텐츠를 구현할 수 있다. 이러한 공간을 위해서는 유비쿼터스(ubiquitous) 환경이 필요하다. 공간에 머무는 사람이 어느 장소에서나 네트워크 컴퓨터를 의식하지 않고 자유롭게 접속할 수 있는 [[정보통신]] 환경이 필요하다. 공간은 다양한 인터랙티브 매체가 적절하게 배치되어 있으며, 이 매체들은 [[유비쿼터스 환경]]에서 유무선 네트워크로 콘텐츠 [[아카이브]]나 [[데이터베이스]] 등에 연결되어 사용자의 [[인터랙티브 행위]]에 따라 서비스 시스템이 통제됨으로 특정 콘텐츠를 제공하는 반응이 일어나는 공간이 진정한 [[제4의 공간]]이라고 할 수 있다. | ||
| + | |||
| + | 최근 전시공간은 제4의 공간으로 가는 중요한 과정이다. 이러한 진보가 이루어진 68 전자통신 동향분석 제29권 제3호 2014년 6월다면, 수용자 대상에 따른 맞춤형 정보 제공이 가능해지고 체험 전시요소가 강화되며, [[실감형 콘텐츠]] 구현도 자유로워질 수 있는 변화가 이루어질 수 있다. 더불어 전시공간에서는 개인화된 [[스마트 디바이스]] 활용과 관련된 기술개발도 활발히 이루어지고 있다. 유비쿼터스 환경 하의 전시공간에서 [[인터랙티브 매체]]와 [[디지털 아카이브]]의 연동, 그리고 개인화된 스마트 디바이스를 활용한 다양한 콘텐츠 서비스까지 가능할 수 있을 것으로 본다. 근대에서 시작된 전시공간은 변화를 계속해 왔고 현재도 어느 때보다도 빠른 속도로 변화하고 있다.<ref name = "메타"></ref> | ||
| + | |||
| + | ===스마트공간 개념=== | ||
| + | [[파일:스마트공간.PNG|썸네일|300픽셀|'''스마트공간 기술의 구성과 범위''']] | ||
| + | [[공간디자인]]의 관점 : 유비쿼터스 기술로 진화되는 공간 환경에서 기존의 공간디자인에서 추구해온 다양한 가치(예를 들면 인간 중심의 공간구성과 동선체계, 심미성, 친환경성 등)를 유지하거나 확대 발전시킬 방안에 대한 논의를 위한 것이다. 이러한 이유로 공간디자인 분야에서의 스마트공간에 대한 연구와 논의는 스마트공간의 특성을 도출하고 스마트공간에서 새로운 디자인 방안을 연구하고 제시하는 논의들이 주를 이루고 있다. | ||
| + | |||
| + | [[정보통신기술]] 분야의 관점 : 스마트공간은 기존의 유비쿼터스 컴퓨팅이 적극적으로 구현된 물리적 공간 정도로 보고 있다. 스마트공간이란 개념 자체의 유용성에 별다른 관심이 없다. 하지만 정보통신기술이 추구하는 유비쿼터스 공간 환경이 인간 생활에 유용한 스마트공간으로 구현되기 위해서는 큰 노력이 필요하다. 유비쿼터스 컴퓨팅으로 구축된 공간에서 사용자인 인간의 편리를 증진하게 시키기 위해선 유비쿼터스 환경에서 콘텐츠 제작 및 서비스 관련 기술이 함께 연구되고 개발돼야 한다. 유비쿼터스는 물리적 공간의 기술환경이고 이를 통해 스마트공간이 완성되기 위해서는 환경에 맞는 콘텐츠 제작, 구축 및 서비스 기술이 필요하다. | ||
| + | |||
| + | 공간디자인 연구 분야에서 꾸준히 연구해 온 스마트공간에 대한 논의 성과도 충분히 받아들여 연구에 활용해야 완성도 높은 스마트공간 구현이 현실성 있게 이루어진다. 스마트공간 기술은 유비쿼터스 컴퓨팅 기술과 유비쿼터스 환경하에서의 디지털콘텐츠 제작 구축 서비스 기술, 그리고 유비쿼터스 환경에 따른 공간디자인 기술이 융합되어 이루어지는 기술이다. 스마트공간이란 지능형 환경을 제공하기 위해 물리적 공간을 구성하는 요소를 컴퓨팅 화하고 네트워킹 화하여, 공간에 있는 사람과 사물들이 그 공간과 전자적으로 소통하는 것을 의미한다. 공간 자체의 인지 상황 정보에 따른 편의 제공과 함께, 떨어진 공간이라도 인지적, 감각적으로 연결되어 [[유기체]]적인 관점으로 구성된 공간이다. 스마트공간은 그 물리 공간을 구성하는 전자적 장치가 아니라 [[물리공간]] 내 사용자의 가치관, 취향, [[상황 목적에 따른 행위에 따라 반응하는 공간]](responsiveenvironments)으로 인간적인 요소가 포함된 개념이고 최적의 편의성을 추구하여 사용자에 제공되는 다양한 콘텐츠와 서비스 시스템까지 포함한다.<ref name = "메타"></ref> | ||
| + | |||
| + | ===전시기술의 트렌드와 스마트공간=== | ||
| + | [[파일:전시공간.PNG|썸네일|300픽셀|'''전시공간 구축 주요 트렌드와 관련 기술''']] | ||
| + | 현대 [[전시공간]]은 [[디지털 기술]]을 어떤 문화산업 분야보다 빠르게 수용하고 있다. 이러한 전시공간의 첨단 기술 수용은 새로운 것을 추구하는 [[전시문화]]의 원형적 특성이 한 원인이다. 지금은 영화와 텔레비전에서 상용화되어 있는 [[쓰리디]] 입체영화도 전시산업에서 시작되었고, [[라이드 필름]](ride simulation film), [[아이맥스 영화]](Imax Large Format film), [[포디]] 영화(4D attractionfilm) 같은 새로운 영상 기술을 적용한 콘텐츠들이 모두 전시공간에서 우선으로 구현됐다. 이런 콘텐츠 기술은 90년대 디지털 기술의 획기적 발전을 통해 진화를 거듭하고 현재는 전시 분야뿐 아니라, 보편적인 문화기술(culture technology)이 되었다. 또한 정보검색 분야에서도 터치 기반의 [[키오스크]](kiosk)부터, [[탈중앙화 신원증명]](DigitalInformation Desk, DID), [[미디어 테이블]](media table) 등으로 발전되었다. 데이터의 기기저장 방식에서 아카이브 연동방식으로까지 진화되고 있다. 새로운 정보통신기술을 가장 먼저 적용하는 산업부문 중 하나가 전시 분야이다. 최근의 전시공간 구축의 주요 트렌드를 보여준다. | ||
| + | |||
| + | 최근 전시공간은 물리적인 공간을 뛰어넘어 [[가상공간]]으로 확장 시켜나가고 있다. [[가상현실]](VirtuaReality, VR)기술, [[증강현실]](Augmented Reality, AR)기술, [[홀로그램]](hologram) 기술, [[사이버(cyber) 전시기술]] 등은 물리적으로 제한된 전시공간에서 차원이 다른 무한의 공간을 창출하고, 현실에서는 경험할 수 없는 초현실적 공간을 연출할 수 있다. 최근 전시공간 구축의 또 다른 기술 트렌드는 이용자 체험성의 강화다. 체험 전시 매체의 발달은 인간의 감각을 확장하는 방향으로 이루어진다. 감각을 확장한다는 것은 두 가지 의미가 있다. 첫째, 특정 감각에 대한 자극을 강하게 한다는 의미와 둘째, 다 감각을 동시적으로 자극한다는 의미이다. 기존 미디어에선 경험할 수 없었던 체험전시에 대한 요구와 오감을 활용하는 실감 콘텐츠에 대한 요구가 전시공간에서의 다 감각 매체 개발과 도입을 지속해서 추구하게 만든다. 또한 최근 전시공간에서는 스마트 디바이스를 활용하는 자동안내 [[시스템]]이 확대되고 있고 디지털 아카이브 서비스는 실물 오브제 전시공간에서 정보검색 서비스를 담당하여 아카이브 서비스 룸을 확장하고, [[웹]]과 [[앱]]에서 아카이브 검색 서비스를 제공하는 방식으로 확대되고 있다. | ||
| + | |||
| + | 디지털 기술은 기존의 전시 매체를 획기적으로 개선해 실물전시 위주의 전시공간을 디지털 매체가 중심인 공간으로 변화하고 있다. 유물 없는 박물관을 가능하게 하고 있고 실물 위주의 기존 아날로그 전시방식을 [[디지로그]](Digilog) 전시나 [[아나탈]](Anatal) 전시라는 새로운 개념의 전시 형태로 전이시키고 있다. 이러한 전시공간 구축기술의 발달은 [[스마트전시]]를 지향하고 있다. 스마트공간 구현에 필요한 유비쿼터스 컴퓨팅을 지향하고 있으며(다양한 [[센싱 기술]]과 [[인터랙티브 기술]] 및 스마트 디바이스 활용기술 등), 디지털 콘텐츠 서비스 기술의 진화도 향상되고 있다. 데이터 연동 콘텐츠 서비스 기술은 이용자 맞춤형 서비스를 가능하게 하고(맞춤형 서비스, 추천기술 및 [[데이터 마이닝 기술]] 등) 체험성이 높은 콘텐츠 기술은 다양한 실감 콘텐츠 서비스를 체험할 수 있게 했다. 특히 시공간 압축을 위한 다양한 가상 콘텐츠 제작 및 서비스 기술 확장은 물리적 공간을 초월한 스마트 전시공간을 지향하는 최근 전시문화의 지향점을 명확히 알 수 있는 지점이다.<ref name = "메타"></ref> | ||
| + | |||
| + | ===스마트전시와 메타버스 서비스=== | ||
| + | [[메타버스]](metaverse)는 [[메타]](meta) + [[유니버스]](universe)를 합친 의미로 우주와 또 다른 차원의 우주, 즉 공간 개념으로 보면 [[현실공간]]과 또 다른 가상의 공간 세계를 칭하는 개념이다. '메타버스는 융합이다. 메타버스는 가상적으로 확장된 물리적 현실과 물리적으로 영구화된 가상공간의 융합이다. 그리고 이용자가 그것을 경험할 때는 동시에 혼재돼서 나타난다'고 정의되고 있다. 3차원 가상공간에 현실을 더함으로써 그 범위를 적극적으로 확장시키고 있는 것이다. 메타버스는 우리의 가상공간과 현실이 적극적으로 상호작용하는 공간이다. 메타버스는 현실과 [[가상세계]]의 교차점이 쓰리디 기술로 구현된 또 하나의 세계를 가리킨다. | ||
| + | |||
| + | 스마트 전시공간에서 메타버스의 구현과 활용은 디지털 콘텐츠 기술 분야의 확장으로 의미를 가진다. 전시공간에서 전시되고 있는 실물 오브제가 디지털 복제를 통해 가상의 쓰리디 그래픽 이미지로 대체될 수 있는 차원을 넘어서 특정 공간을 메타버스로 구현한다면 그 공간은 수많은 오브제와 관련 콘텐츠를 담아낼 수 있는 획기적인 [[메타콘텐츠]](metacontents)가 될 수 있을 것이다. 메타버스는 전시공간과 관련한 고도의 추상 세계인 [[버추얼 세계]](virtual world)가 될 수 있고 전시공간을 그대로 복제한 거울 세계(mirror world)가 될 수도 있다. 그리고 두 메타버스 사이에 다양한 추상성 층위의 융합 개념 메타버스가 구현가능할 것이다. 이를 토대로 전시공간에서 메타버스의 활용은 전시공간의 확장은 물론 전시 아이템의 무한한 확장을 가능하게 한다. 메타버스 개발 및 서비스 기술은 스마트 전시공간의 콘텐츠 기술에 중요한 요소가 된다. 예를 들어 하나의 전시 오브제인 공룡의 뼈 화석으로부터 그 공룡이 살고 있었던 수백만 년 전 세계를 메타버스로 구현하여 화석이 된 공룡과 관련 이야기를 콘텐츠화해 메타버스 서비스를 할 수 있다. 이러한 콘텐츠 장르로는 [[팩션]](faction)이 될 것이며 메타버스는 버추얼(virtual) 공간이 될 것이다. | ||
| + | |||
| + | 메타버스의 구현은 쓰리디 그래픽을 활용한 리얼리티 구현이 기본적인 개념이라고 할 수 있다. 하지만 전시 목적과 환경에 따라 다양한 수준의 구현기술 적용이 가능하다. 또한 이 메타버스에 대한 서비스 형태도 서비스 기술에 따라 다양한 수준에서 이루어진다. 먼저 메타버스에 아바타를 전송 시켜 플레이하는 [[가상체험]] 형식의 서비스가 메타버스의 기본적인 서비스 형태나, 과도기적인 현황에서 메타버스 콘텐츠를 단순히 선택적 관람을 하는 방식으로 콘텐츠 서비스가 제한될 수도 있다. 콘텐츠 서비스 기술은 전시 매체 관련 기술, 서비스 장치, 전시공간의 통신환경 등 다양한 환경 조건에 따라 결정된다.<ref name = "메타"></ref> | ||
| + | |||
| + | [[파일:그림3.PNG|썸네일|200픽셀|'''유사 증강현실 화면 배경 변환 및 쓰리디 애니메이션으로 메타버스''']] | ||
| + | ;유사 사례: 베를린 자연사 박물관(Museum für Naturkunde) | ||
| + | {{테두리색|#fff0f5|* 오브제(공룡 뼈)를 연동한 메타버스 구현 | ||
| + | * 공룡 뼈 구조물을 고글을 통해서 보면 공룡이 살아 움직이는 가상현실 영상이 보이는 전시 기법 | ||
| + | * 박물관 입구 중앙 홀 화석으로 맞추어진 공룡 골조 구조 전시공간 | ||
| + | * 주변에 유사 [[증강현실]] [[고글형 디바이스]] 10여 대 설치 | ||
| + | * 고글형 이외에, 대상 지적 - 오픈 모니터형 시스템도 4곳에 설치되어 운영 | ||
| + | * 유사 증강현실 시스템이 대상 공룡에 맞춰지면 → 공룡의 장기 → 근육 → 피부 생성 → 영상 화면 배경이 야외 공룡 생태 환경으로 변함 → 공룡이 살아서 움직임}}<ref name = "메타"></ref> | ||
| + | |||
| + | ===메타버스 기반 스마트 전시 안내 시스템 개발=== | ||
| + | [[파일:그림4.PNG|썸네일|300픽셀|'''스마트 디바이스 - 전시 미디어 연동 시스템(MMOID)''']] | ||
| + | 방문객이 즐겁게 전시공간을 관람하게 하기 위해서 입장 전에 관람객 머릿속에 전시공간의 맵을 인지시켜야 한다. 움직이는 동선에 대한 불안감 없이 공간을 관람할 때 집중도가 높아지고 효율적인 관람이 이루어질 수 있다. 그래서 방문객들은 어김없이 입구에서 전시공간의 맵을 찾는다. 그런데 공간이 넓거나 실내와 실외 공간을 오가는 복잡한 구조의 공간이라면 단순히 방문객에게 맵을 주는 것으로는 부족하다. 메타버스 기반 스마트 전시 안내 [[시스템]] 개발 과제는 전시공간의 메타버스 - 거울 세계를 구축하고 방문객들이 메타버스에서 아바타 가상투어를 하도록 유도한다. 이를 통하여 방문객들 머릿속에 공간의 맵을 인지 시켜 실제 공간에 나아가도록 하기 위한 서비스 기획이다. 또한 이용자의 체험성을 높이고 [[엔터테인먼트]] 요소를 강화하기 위한 기획이기도 하다.<ref name = "메타"></ref> | ||
| + | |||
| + | ;시스템 특징 | ||
| + | {{테두리색|#fff0f5|* 중대형 실내형 전시공간, 야외형 전시공간, 전주 한옥마을과 같은 곳에 가이드 시스템으로 활용 가능한 서비스와 황룡사, 미륵사지와 같은 사라진 문화 유적지에 대한 가상공간 복원 및 가상투어를 통한 [[전시 가이드 시스템]]으로 활용도가 높을 것으로 기대한다. | ||
| + | * [[스마트]] 디바이스 [[앱]]과 전시 미디어가 연동하는 전시 안내 시스템으로 모바일과 위치 기반 미디어 특성을 연동하는 다양한 서비스 시나리오를 구현하는 기술 | ||
| + | * 개인의 스마트 디바이스에서 생성한 아바타를 전시 미디어에 포팅(porting)하고 컨트롤하여 인터랙티브 방식의 전시 안내 서비스를 받는 기술 | ||
| + | * 전시 미디어에 전시공간 전체 맵이 쓰리디 기반의 메타버스로 구현되고, 관람자가 앱에서 생성한 자신의 아바타를 전시 미디어로 전송하고 메타버스를 가상 투어하여 필요한 정보와 아이템들을 획득해 자신의 스마트 디바이스에 받음. | ||
| + | * 메타버스 가상투어는 동시에 다수의 이용자(현재 40명 동시접근 구현)가 참여할 수 있고 참여자들은 서로 실시간 채팅 형식의 대화를 나눌 수 있다. | ||
| + | * 실제 전시공간에 앱을 활성화한 채 관람을 하는 이용자는 자신의 위치에서 생성한 콘텐츠(사진, 텍스트 등)를 올릴 수 있고 업로드된 콘텐츠는 메타버스 내 같은 위치에 누적되며, 업로드 정보가 메타버스 내 위치에 남는다.}} | ||
| + | ;개발 예정 | ||
| + | {{테두리색|#fff0f5|* 개발 예정: 익산 미륵사지 메타버스 안내 시스템 개발 | ||
| + | * 익산 미륵사지의 7세기 [[디지털]] 복원 이미지를 기반으로 메타버스 구축 | ||
| + | * [[메타버스 아바타]] 가상투어 플레이를 통해 건물에 대한 이미지와 정보 숙지 | ||
| + | * 앱 활성화 상태에서 야외 미륵사지 투어 시 콘텐츠 업로드 및 위치별 증강현실 콘텐츠 서비스 }}<ref name = "메타"></ref> | ||
| + | |||
| + | 현대의 전시산업은 근대 생성 이후 첨단기술을 가장 빠르게 수용하여 전시공간을 구축과 운영하며 발전시켜왔다. 1990년대 이후 [[정보통신기술]]의 급속한 발전은 전시공간을 유비쿼터스 컴퓨팅 환경과 다양한 디지털 콘텐츠 구현 및 서비스 기술의 상호적 발전과 더불어 전시공간의 스마트공간 화를 가능하도록 했다. 전시공간에서 메타버스 개념의 적용은 전시공간의 물리적 한계를 넘어서는 획기적인 전시 방법의 대안이 될 수 있으며, 전시공간을 스마트공간으로 확장하는 중요한 분야임을 알았다. 미래부 과제로 진행되는 메타버스 기반 스마트 전시 안내 시스템개발에서 [[스마트 디바이스 - 전시 미디어 연동 시스템]](MMOID)을 활용한 메타버스 가상체험 전시안내 시스템개발은 현재의 전시공간 기술 수준을 향상할 수 있는 잠재적 외연이 넓은 기술개발 과제임을 숙지하길 바란다. <ref name = "메타"></ref> | ||
| + | |||
| + | ==자동차 실내 공간== | ||
| + | * '''[[헤드룸]]''' : 탑승자가 시트에 착석한 상태에서 머리 위 공간을 가늠할 수 있는 수치를 의미한다. 시트의 힙 포인트에서 헤드라이닝까지의 거리를 측정해 표기한다. 미국자동차공학회(SAE) 기준으로는 힙포인트에서 헤드라이닝까지의 측정값에 102mm(4인치)를 더한 수치를 발표치로 한다. | ||
| + | * '''[[숄더룸]]''' : 탑승자가 시트에 앉았을 때 어깨 공간을 확인할 수 있는 수치다. 좌측 도어 트림부터 우측 도어 트림의 상부(팔거치부 위쪽)간 최소 수평거리를 측정해 표기한다. 실제 승차 시 너비 공간을 가늠할 수 있다. 주로 도어트림 상부 형상에 따라 수치가 달라진다. | ||
| + | * '''[[레그룸]]''' : 탑승자의 다리 여유 공간을 나타낸 수치로, 실내 공간 크기 수준을 가늠할 수 있는 주요 수치로 여겨진다. 보통 시트의 힙 포인트부터 발을 최대한 뻗을 수 있는 곳까지의 수치를 측정해 표기한다. 미국자동차공학회(SAE) 기준으로는 힙포인트에서 발목까지의 측정값에 254mm(10인치)를 더한 수치를 발표치로 한다 | ||
| + | * '''[[풋룸]]''' : 일반적으로 승객의 발을 두는 공간을 의미한다. 전석 보다는 후석의 풋룸을 중요시 하는데, 2열의 풋룸은 1열 시트 하단부 구조물에 의해 좌우폭과 높이에 따른 공간이 결정되며 시트 하부에 발을 뻗을 수 있는 정도에 영향을 주기 때문에 후석 레그룸에 영향을 준다. | ||
{{각주}} | {{각주}} | ||
| 26번째 줄: | 342번째 줄: | ||
* 〈[https://namu.wiki/w/%EA%B3%B5%EA%B0%84 공간]〉, 《나무위키》 | * 〈[https://namu.wiki/w/%EA%B3%B5%EA%B0%84 공간]〉, 《나무위키》 | ||
* 〈[https://terms.naver.com/entry.naver?docId=1717441&cid=41908&categoryId=41972 공간]〉, 《네이버 지식백과(현상학 사전)》 | * 〈[https://terms.naver.com/entry.naver?docId=1717441&cid=41908&categoryId=41972 공간]〉, 《네이버 지식백과(현상학 사전)》 | ||
| − | * | + | * 〈[https://ko.wikipedia.org/wiki/%EB%B0%94%EB%82%98%ED%9D%90_%EA%B3%B5%EA%B0%84 바나흐 공간]〉, 《위키백과》 |
| + | * 〈[https://ko.wikipedia.org/wiki/%EC%9C%A0%ED%81%B4%EB%A6%AC%EB%93%9C_%EA%B3%B5%EA%B0%84 유클리드 공간]〉, 《위키백과》 | ||
| + | * 〈[https://ko.wikipedia.org/wiki/%EA%B1%B0%EB%A6%AC_%EA%B3%B5%EA%B0%84 거리 공간]〉, 《위키백과》 | ||
| + | * 〈[https://ko.wikipedia.org/wiki/%ED%9E%90%EB%B2%A0%EB%A5%B4%ED%8A%B8_%EA%B3%B5%EA%B0%84 힐베르트 공간]〉, 《위키백과》 | ||
| + | * 〈[https://ko.wikipedia.org/wiki/%EB%B2%A1%ED%84%B0_%EA%B3%B5%EA%B0%84 벡터 공간]〉, 《위키백과》 | ||
| + | * 〈[https://ko.wikipedia.org/wiki/%EC%82%AC%EC%98%81_%EA%B3%B5%EA%B0%84 사영 공간]〉, 《위키백과》 | ||
| + | * 〈[https://ko.wikipedia.org/wiki/%EC%9C%84%EC%83%81_%EA%B3%B5%EA%B0%84_(%EC%88%98%ED%95%99) 위상 공간]〉, 《위키백과》 | ||
| + | * 〈[https://ko.wikipedia.org/wiki/%ED%99%95%EB%A5%A0_%EA%B3%B5%EA%B0%84 확률 공간]〉, 《위키백과》 | ||
| + | * 〈[https://ko.wikipedia.org/wiki/%EC%8B%9C%EA%B0%84%EA%B3%BC_%EA%B3%B5%EA%B0%84%EC%9D%98_%EC%B2%A0%ED%95%99 시간과 공간의 철학]〉, 《위키백과》 | ||
| + | * 〈[https://ko.wikipedia.org/wiki/%EA%B0%80%EC%83%81_%EA%B3%B5%EA%B0%84 가상 공간]〉, 《위키백과》 | ||
| + | * 김성희·이현우·류원·김광신, 〈[https://www.koreascience.or.kr/article/JAKO201452057196673.pdf 스마트공간과 메타버스 전시안내 기술개발 동향]〉, 《전자통신동향분석 제29권 제3호》, 2014-06 | ||
==같이 보기== | ==같이 보기== | ||
* [[시간]] | * [[시간]] | ||
* [[시공간]] | * [[시공간]] | ||
| + | * [[가상공간]] | ||
| + | * [[메타버스]] | ||
| − | {{메타버스 | + | {{우주|검토 필요}} |
| + | {{메타버스}} | ||
2023년 1월 30일 (월) 17:48 기준 최신판
공간(space, 空間)은 어떠한 물질 또는 물체가 존재할 수 있거나 어떠한 일이 발생할 수 있는 장소이다. 사람이나 사물이 차지 하는 장소 또는 인간의 활동이 행해지는 장이나 물체의 운동이 그 속에서 전개되는 넓이를 의미하기도 한다. 공간은 물질이 존재하고 여러 가지 현상이 일어나는 장소이다.[1][2][3] 공간에서 특정 위치는 가로, 세로, 높이의 3가지 좌표를 이용해 표시할 수 있다. 이런 점에서 공간을 3차원 공간이라고도 한다.
목차
개요[편집]
공간의 성질에 대한 이해를 시도하는 것은 철학자와 과학자들에게 항상 어려운 숙제였다. 많은 토론의 결과에도 불구하고 공간에 대한 논쟁은 끊임없으며, 명확하고 확실한 정의를 제공하는 것은 어려운 일이다. 공간은 물리학자, 철학자, 수학자, 종교인에 의해 다양하게 다루어지고 공간과 마음 사이의 관계에서도 다양한 관점이 있다. 더불어 다양한 공간의 존재 방식이 있다는 것을 알 수 있다.[2]
공간의 존재 방식[편집]
물체와 그 운동[편집]
- 고대 원자론자 : 아무것도 없는 공허한 것이다.
- 데카르트 : 연장, 넓이가 물체의 본질이기 때문에 물체와 공간은 동일한 것이다.(이러한 생각에서 기하학과 물리학이 동일화된다.)
- 아리스토텔레스 : 공간은 사물들이 인접하는 경계, 따라서 사물을 받아들이는 용기와 같은 것인 장소의 총화이다.
- 라이프니츠 : 공간은 물체와 독립하여 존재하지 않고 사물과 사물의 상호 관계의 총체에 지나지 않는다.
위의 주장들과 관련하여 공간은 유한한가 무한한가 또 등질, 등방인가 아닌가와 같은 것도 논의가 있었지만, 주목을 끈 것은 고대와 중세에는 이 우주 공간이 지구를 중심으로 하여 항성천에 의해 한계 지어진 유한한 세계고 나아가 달 아래의 세계는 천상의 세계와 질적으로 다르고 무거운 물질이 중심을 향하는 것으로 특징이 지어짐으로써 공간에 방향성이 주어진 데 반해, 근세의 과학의 견해에서는 공간이 등질적이며 무한한 것으로 보았다. 19세기에 확립된 전자장 이론에서는 공간의 이질 이방성이 다시 제기되었고 아인슈타인의 일반 상대성 이론에서는 이 세계의 유한성이 주목되었다. 더불어 기하학과 물리학의 일체화라는 데카르트적인 생각이 다시 알려지며 재평가 되었다.[3]
인간과 그 활동[편집]
인간과 인간의 활동 존재 방식과 관련하여 공간은 생활공간, 도시공간, 환경 공간 등으로서 물체와 그 운동에 관련된 공간과 다르게 정의적 가치와 결부된 의미 공간을 규정된다. 예를 들어서 사람과 사람의 대면 상의 거리는 물질적인 거리에만 멈추지 않고 인간관계의 친소, 사회 신분상의 차이에 따라 변하는 심리적 거리도 반영한다. 지각 심리학이나 문화 인류학의 깨달음과 인간과 동물의 행동 양식은 같고 다름과 같은 정신병리학적 현상 등에 대한 고찰로부터 인간적 공간의 특성이 다양하게 제시되어 왔다.[3]
현상학에서의 공간[편집]
현상학에선 공간도 인간의 존재 방식과 상관적으로 다루어지기 때문에 인간적 공간만이 의미 공간인 것이 아닌 물리학적 공간, 수학적 공간도 인간의 의식에 의해 구성된 의미 공간이라고 칭한다. 공간의 의미의 중층적 구조가 분석, 해명되는데 여기선 공간이 지각된다. 그로 인해 행동이 행해지는 구체적 공간과 이념화하는 추상에 의한 극한 개념(점, 선, 면 등)이 설정되어 이것을 기초로 하여 전개되는 이념적 공간이 구별된다. 구체적 공간은 기저층으로 공간적 위상을 기초로 하여 구성되고 이념적 공간은 기호를 매개로 하여 형식화하는 조작에 의한 형식적 수학적 공간과 실질적 물리학적 공간을 나누어진다.[3]
전공간적 위상[편집]
지각에는 감각이 휠례적 계기로서 포함된 것처럼 전공간적 영역은 구체적 공간에 대해 생기가 불어넣어지고 통각이 되기 이전의 내재적 영역이다. 이것은 감각장(시각장, 청각장, 촉각장)과 기관 운동장(안구 운동장, 촉각 운동장)으로 나누어진다. 감각장은 중심을 지닌 원 형상의 불명확하게 경계 지어지는 2차원 연속체이며 중심과 주변이라는 위치 체계가 보이고 변화가 있지만, 어떠한 운동도 존재하지 않는다. 기관 운동장은 '나는 움직인다'라는 의식의 근거를 형성하는 운동 감각적 소여에 기초하는 것으로서 자세나 운동의 빠르기 또는 가속의 감각, 긴장감 나아가서 이들에 수반되는 고통감 등이 여기에 속한다.
예를 들어 감각장의 어떤 형태의 변화가 형태 자신의 변화인가 아니면 나에 대한 위치의 이동에 의한 변화인가 하는 것은 '내가 움직인다'에 의해 그 변화가 본래대로 되돌려지는가 아닌가에 의해서 결정된다. 이를 통해 감각적인 합동 이동과 기관 운동적인 운동이 구별되고 중심, 주변이라는 위치에 체계가 임의로 움직여질 수 있게 되면 눈은 그 육체성을 제거당해 시광전행의 비물체적 기관이 되고 기관 운동장은 시광운동장이 된다. 신체 구성의 중요한 계기인 이중감각은 이러한 영역의 특이 현상이다.[3]
구체적 공간[편집]
이 공간은 체험된 공간 또는 생활 공간이라고도 불리지만, 그에 대한 해명은 후설의 지각이론과 하이데거의 현 존재의 공간성에 대한 분석 및 메를로, 퐁티의 신체론을 정초적인 업적을 하여 진전되어 왔다. 이 공간은 인간의 지정의라는 존재 방식에 대응하여 표상적, 상모적, 행동적인 세 가지 국면을 지니고 이 세 가지가 통합된 것이지만 그때마다 두드러진 국면을 따라서 직관적(표상적) 공간, 상모적(기분 지어진) 공간, 행동(행위) 공간으로 나누어질 수 있다. 행동 공간에서는 상하, 좌우, 전후라는 방향성이 두드러져 보이지만 그것은 신체의 기능성에 의한 바가 크다. 상모적 공간에선 이러한 방향성이나 표상 공간에서의 퍼스펙티브라는 것이 보이지 않고 등방도 이방도 아니면 무방(無方)이고 분위기적이다. 종교적 내지는 축제적인 성스러운 공간이나 예술적 공간은 다분히 상모적 공간에 따른다. 표상적 공간에서는 신체가 놓여 있는 여기를 원점으로 하는 깊이와 퍼스펙티브가 주목되는 현상이지만, 다른 공간과는 달리 이 공간은 미세하게 구조화되어있고 공간의 장소도 점적인 것으로까지 줄어들 수 있다. 더 나아가 시점(視點)과 장소의 이동에 의해서 신체라는 표상 공간 내의 중심점이 탈중심화되어 상호주관적인 공동공간이 구상되며 이념화에 의해 극한의 형태가 선취되어 이념적 공간이 성립된다.[3]
형식적, 수학적 공간[편집]
예를 들어 곡면상에서 직선을 그을 수 있는가(원주면이나 원추면 등) 없는가(구면이나 의구면 등)와 같은 위상적인 성질과 전곡률이라고 불리는 공간의 일그러짐 정도는 그 곡률이 일정한지 아닌지 하는 계량 관계에 의해 분류된다(유클리드 공간, 타원 공간). 그때 공간론의 전개는 몇 가지 수학적 절차에 기초한다. 기호를 매개로 한 형식화의 조작에 의해 수행되는 것(기하학의 대수화), 곡률의 판정이 근방이라는 극미의 범위에서 성립하는 것(미분기하학) 등이 이것들이다. 즉 수학적 공간은 이념화와 형식화의 조작에 의해 구성되지만 그러한 조작에는 수학적 귀납법에서 나오는 회귀적(반복 가능성의) 법칙성에 의한 무한의 과정의 선취라는 것이 따라다닌다. 예를 들어 이념적 존재인 수학적인 점은 구성이 완결되지 않는 한에서 구성 가능한 형성체라는 역설적인 의미가 있다.[3]
실질적, 물리학적 공간[편집]
표상 공간의 이념화에 의해 얻어지는 공간은 유클리드 공간이지만 이것은 실질적 공간(유클리드 기하학에서의 공간)이어서 수학에서 형식화된 유클리드 공간과는 구별된다. 이에 대해 고전 물리학에서 공간은 공간을 채우는 질(질량, 강체, 온도 등)이 그것에 짜 넣어진다는 것과 질의 규정이 인과성을 기초로 한다는 것(예를 들어 체적/온도 = 일정에 의한 온도의 규정)에 놓여있다. 결국 고전 물리학에서의 공간은 물질적, 인과적 사물과 유클리드 공간이 종합된 데서 성립한다. 그때 사물의 길이가 장소와 이동에 의해 변하지 않는다(기하하적으로 합동 변환이 성립한다는 것)고 하는 것에서 전형적으로 보이듯이 공간과 사물은 상호작용이 없는 것, 독립된 것으로 여겼다. 현대 물리학에서 공간은 시간과 일체화된 4차원 시공으로서 통합되고 고전 물리학에서의 자연의 인과성에 대해 의문이 들며 물질로부터의 공간 독립성이 포기되었지만, 시공적인 장과 물질이 어떻게 관계 지어지는지에 관한 물음은 해결되지 않고 있다.[3]
물리학에서의 공간[편집]
물리학에서 공간의 정의는 여러 이론이 있다. 다음과 같이 다양한 개념으로 공간의 정의를 시도한다.
- 물체 사이의 공간적 관계의 집합으로써 정의되는 구조
- 물체가 있는 좌표계에 의해 정의되는 다양체
- 한 물체를 다른 물체와 분리되어 존재하게 하는 것
고전 물리학에서 공간은 어느 한 위치가 3개의 좌표축에 의해서 기술되는 3차원 유클리드 공간이다. 상대론적 물리학에서는 공간보다 시공간을 더 고찰한다. 시공간은 4차원의 다양체로 모형화 되었으며, 요즘에는 그 이론이 11차원까지 여겨지고 있다.
아인슈타인의 상대론적인 물리학 연구 이전에는 시간과 공간은 서로 독립적인 차원이라고 여겼으며 아인슈타인의 연구는 시간과 공간을 하나의 시공간을 통합했다. 시공간에서 시간과 공간의 측정은 속도에 상대적이다.[1]
공간의 차원[편집]
공간의 차원은 생물학을 비롯하여 물리법칙에 큰 영향을 끼친다. 2차원 이하의 생명체는 지능을 가질 수 없다고 여기고 3차원에선 뉴런이 임의의 수의 뉴런과 연결될 수 있지만, 2차원에서는 신경이 교차할 수 없음으로 이것은 불가능하다.
가우스 법칙에 따라 2차원 이하에서는 거리가 커질 때 퍼텐셜 발산하고 이로 인해 행성의 궤도는 언제나 속박되어 있으며 원자의 이온화도 불가능하다. 3차원에서는 유효퍼텐셜이 아래로 볼록하여 근일점과 원일점 사이를 오가는 안정한 궤도가 가능하다. 4차원에서 천체는 원 궤도만 가능하고 타원 궤도는 불가능하다. 5차원 이상은 유효퍼텐셜이 위로 볼록하여 천체는 궤도를 이루지 못한다.
디랙 방정식을 고려하였을 때, 4차원 이상에서는 안정한 수소 원자 모형이 존재하지 않는다.
짝수 차원에서는 파동이 0~c의 다양한 속도로 전파되어 다른 시간에 생긴 파동이 동시에 도달하는 문제가 발생한다. 홀수 중에서도 1, 3차원에서만 파동이 파원의 진폭에 정확히 비례하는 방식으로 전달된다.[2]
천문학에서의 공간[편집]
천문학에서 공간은 우주의 빈 부분을 통합하여 이야기한다. 천체의 대기권 바깥 부분을 공간이라고 말할 수 있다. 우주 공간과 지구의 대기권 사이의 경계는 통상적으로 카르만 선에서 정해진다.[1]
수학에서의 공간[편집]
수학에서 공간은 몇 가지의 특별한 속성과 부가적 구조를 가지는 집합이다. 가끔 공간은 벡터 공간 또는 자기 자신의 특이한 변형이다.[1]
바나흐 공간[편집]
함수 해석학에서 바나흐 공간(空間, Banach space)은 완비 노름 공간이다. 스테판 바나흐의 이름을 따왔다.
- 정의
-노름 공간 에 대하여 다음 두 조건이 서로 동치이고, 이것을 만족시키는 -노름 공간을 -바나흐 공간이라고 한다.
- 노름으로 정의한 거리 함수를 부여하게 되면, 완비 거리 공간이다. 모든 코시 열이 수렴한다.
- 모든 절대 수렴 급수가 수렴한다. 임의의 점렬 에 대하여, 만약 라면, 급수 역시 노름으로 정의한 거리 위상에 대해 수렴한다.
체 를 실수체 혹은 복소수체로 국한하는 이유는 노름 공간에 완비성을 가정하려면 그 체가 완비되어야 하기 때문이다. 예를 들어서 유리수체는 완비되지 못한다.[4]
유클리드 공간[편집]
수학에서 유클리드 공간(Euclidean space)은 유클리드가 연구했던 평면과 공간을 일반화한 것이다. 일반화는 유클리드가 생각했던 거리와 길이와 각도를 좌표계에 도입하여 임의 차원의 공간으로 확장한 것이다. 이것은 표준적인 유한 차원, 실수, 내적 공간이다. 때에 따라 민코프스프키 공간에 대비되는 주장으로 피타고라스의 정리에 의한 길이 소의 제곱 계수가 모두 양수인 공간을 말한다.
- 정의
음이 아닌 정수 에 대해 차원 유클리드 공간 은 집합으로서 실수 집합 의 번 곱집합이다.
이 위에 내적
- 를 정의하면,
은 실수 힐베르트 공간을 이룬다. 이에 따라서 유클리드 공간은 내적 공간, 바나흐 공간, 노름 공간, 벡터 공간, 완비 거리 공간, 위상 공간을 이룬다.
자명한 좌표근방계를 주어서 매끄러운 다양체 및 리만 다양체로 만들 수 있다. 이러한 겨우, 리만 계량으로 정의한 거리는 내적으로 정의한 거리와 일치하다.[5]
힐베르트 공간[편집]
함수 해석학에서 힐베르트 공간(Hilbert space)은 모든 코시 열의 극한이 존재하는 내적 공간이다. 유클리드 공간을 일반화한 개념이다.
- 정의
가 또는 라고 할 때, -힐베르트 공간 은 완비 거리 공간을 이루는 -내적 공간이다. 내적 공간인 힐베르트 공간은 표준적인 위상 공간, 거리 공간, 벡터 공간, 노름 공간 중에서 원하는 구조를 갖는다.
이와 논리가 같은 것으로, -힐베르트 공간을 다음과 같은 평행사변형 항등식을 만족시키는 -바나흐 공간 으로 정의할 수 있다.
이러한 경우 내적 구조는
- 가 된다.
거리 공간[편집]
수학에서 거리 공간(metric space)은 두 점 사이의 거리가 정의된 공간이다. 거리의 정의에 따라 표준적인 위상을 가진다.
- 정의
집합 위의 거리 함수는 다음 조건을 만족시키는 함수 이다.
- 구분 불가능한 점의 동일성인 임의의 에 대해서
- 대칭성인 임의의 에 대해서
- 삼각 부등식인 임의의 에 대해서
마지막 두 공리는 다음과 같은 하나의 공리로 바꿀 수 있다.
여기서 로 설정하면, 가 되어, 대칭 공리를 얻는다. 거리 함수의 정의에서, 첫째 조건을 로 약화시키게 되면 유사 거리 함수의 개념을 얻는다. 거리 공간 은 거리 함수가 주어진 집합이다.[6]
벡터 공간[편집]
선형대수학에서 벡터 공간(vector space) 또는 선형 공간(linear space)은 원소를 서로 더하거나 주어진 배수로 늘이거나 줄일 수 있는 공간이다. 체에 대한, 가군의 특수한 경우이다. 벡터 공간의 원소를 벡터라고 하고 이것은 직관적으로 방향 및 길이의 비가 정의된 대상을 나타낸다. 그러나 노름이 주어지지 않은 일반적인 벡터 공간에서는 벡터의 길이 자체는 정의되지 않는다.
- 정의
체 위의 벡터 공간 은 에 대한 가군 이다. 다음과 같은 튜플이다.
이와 같은 데이터는 다음과 같은 공리들을 만족시켜야 한다.
- 는 아벨 군을 이루고 다음과 같은 성질들이 성립한다.
- 는 의 가군을 이루고 다음과 같은 성질들이 성립한다.
- 임의의 및 에 대해서
- 임의의 에 대해서 . 여기서 는 의 곱셈 항등원이다.
- 분배 법칙인 임의의 및 에 대해서
실수체 에 대한 벡터 공간을 실수 벡터 공간(real vector space)이라 칭하고 복소수체 에 대한 벡터 공간을 복소수 벡터 공간(complex vector space)이라고 칭한다.[7]
사영 공간[편집]
수학에서 사영 공간(projective space, 射影空間)은 벡터 공간의 원점을 지나는 직선들의 집합이다. 평행선들이 만나는 장소인 무한 원 직선이나 무한 원 평면 등의 개념을 다루기 위해서 만들어진 개념이다. 사영 공간의 기하학을 다루는 학문인 사영기하학은 현대 대수기하학의 기초가 되었고 사영 공간 및 이를 확장한 개념인 그라스만 다양체와 깃발 다양체는 위상 수학, 리 군론, 대수 군로 및 이 대상들의 표현론에서 중요한 역할을 맡는다.
- 정의
음이 아닌 정수 이 주어졌다고 가정했을 때, 정수 계수의 차원 사영 공간 은 다음과 같다.
여기서 은 등급환인 정수 계수 다항식환이며, 는 사영 스펙트럼이다.
임의의 스킴 에 대해서 좌표의 차원 사영 공간 은 다음과 같다.
여기서 는 스킴의 범주의 곱을 뜻한다.
만약 가 가환환이라면 다음이 성립한다.
가 대수적으로 닫힌 체라고 했을 때, 의 닫힌 점들은 다음과 같이 구체적으로 정의할 수 있다. 에 다음과 같은 동치 관계를 준다.
그렇다면 의 닫힌 점들은 동치류 집합 에 대응한다. 이러한 경우, 을 동차좌표라고 한다.[8]
위상 공간[편집]
일반 위상 수학에서 위상 공간(topological space, 位相空間)은 어떤 점의 근방이 무엇인지에 대한 정보를 담고 있지만, 점 사이의 거리, 부피, 넓이의 정보를 포함하지 않는 공간이다. 이것을 사용하여 함수의 연속성이나 수열의 극한, 집합의 연결성 등을 정의할 수 있다. 위상 공간의 개념은 위상 수학 및 이를 기초로 하는 기하학, 해석학에서 핵심적으로 사용된다. 위상 공간의 일반적인 성질을 연구하는 분야가 일반 위상 수학이다.
- 정의
집합 위의 위상은 다음과 같이 여러가지로 정의할 수 있다.
- 열린집합을 사용한 정의: 다음 조건을 만족 시키는 부분 집합들의 모임 . 이러한 경우 의 원소들을 열린집합이라고 한다.
- 만약 라면,
- 만약 라면,
- 닫힌집합을 사용한 정의: 다음 조건을 만족 시키는 부분 집합들의 모임 . 이러한 경우 의 원소들을 닫힌집합이라고 한다.
- 만약 라면,
- 만약 라면,
- 근방을 사용한 정의: 다음 조건을 만족 시키는 함수 . 이러한 경우 로 쓰고, 의 원소를 의 근방이라 한다.
- 모든 에 대해서,
- 모든 에 대해서, 만약 라면
- 만약 이며 라면,
- 만약 라면
- 만약 라면, 인 가 존재한다.
- 폐포를 사용한 정의: 다음 조건을 만족 시키는 함수 . 이러한 경우 를 의 폐포 라고 한다.
- 모든 에 대해서
- 모든 에 대해서
- 모든 에 대해서
- 내부를 사용한 정의: 다음 조건을 만족 시키는 함수 . 이러한 경우 를 의 내부라고 한다.
- 모든 에 대해서
- 모든 에 대해서,
- 모든 에 대해서
이 정의들은 서로 동치이다.
- 열린집합을 사용한 정의에서,
- 닫힌집합을 사용한 정의에서, 열린집합은 닫힌집합의 여집합이다.
- 근방을 사용한 정의에서, 열린집합은 인 집합 이다.
- 폐포를 사용한 정의에서, 열린집합은 인 집합 이다.
- 내부를 사용한 정의에서, 열린집합은 인 집합 이다.
결과적으로 근방 · 열린집합 · 닫힌집합 · 폐포 · 내부 가운데 하나를 기본 무정의 개념으로 삼고, 이로부터 나머지 개념들을 정의할 수 있다.
위상 공간은 위상을 갖춘 집합이다.[9]
확률 공간[편집]
확률론에서 확률 공간(probability space, 確率空間)은 천체 측도가 1인 측도 공간이다. 확률적인 현상에서 확률 공간의 측도는 확률을 정의 한다.
- 정의
확률 공간 은 공간 전체의 측도가 1인 측도 공간이다.
확률론에서는 측도론의 용어와 다른 각종 용어들이 이용된다.
확률론의 용어를 사용하게 되면 측도 공간의 각종 성질은 다음과 같다.
- 사건 에 대해서 그 여집합 역시 사건이다. 어떤 사건에 대하여, 그 사건이 일어나지 않는 경우 역시 사건이다.
- 가산 개의 사건들이 주어졌을 때, 그 합집합과 교집합 역시 사건이다. 사건들의 열이 주어졌을 때, 사건의 열 가운데 적어도 하나가 일어나는 경우(합집합)도 사건을 이루며, 사건의 열이 모두 일어나는 경우 (교집합) 또한 사건을 이룬다.
- 공집합과 전체 집합은 사건이다. 불가능한 사건(공집합)과 필연적인 사건(전체 집합)이 존재한다.[10]
불교에서의 공간[편집]
불교에서의 공간은 모든 유위, 무위법이 존재한다. 활동하는 장소인 무위법으로서의 절대 공간에 해당하는 허공(虛空) 또는 허공 무위(虛空無爲)와 유위법이면서 가법인 심불상응행법에 속한 방위와 방향, 공간으로서의 방(方)을 구분한다. 불교 일반에서는 시(時), 시간과 과거, 현재, 미래에 대해서는 실재하지 않는 법을 마치 실재법인 것처럼 삼은 것이라고 본다. 이것을 가법이라고 한다.
부파불교의 설일체유부에서는 절대 공간인 허공이 별개의 실체, 실법이라 한다. 반면에 대승 불교에선 절대 공간인 허공을 진여의 한 측면이라고 보고, 진여라는 실법에 근거하여 가립한 가법이라고 한다. 하지만 절대 공간을 부파 불교에서와 마찬가지로 허공 무위라고 칭한다. 불교 일반에서는 마음(6식 또는 8식, 심왕, 심법)은 무위법이 아닌 유위법이라고 보며 마음을 온갖 심소법(心所法)들, 즉 선(善) · 불선(不善) · 무기(無記)의 온갖 마음의 작용들이 일어나고[生] 작용하고[住] 사라지는[滅] 변화하고[異] 장소 또는 공간이라는 뜻에서 지(地)라고도 칭한다.[1]
철학에서의 공간[편집]
시간과 공간의 철학으로는 아래와 같은 물음이 고찰되고 있다.
- 시간이나 공간은 그중에 있는 물체와 독립에 실재하는가 아니면 어디까지나 물체의 관계로만 존재하는 것인가?
- → 시간의 반실재론으로는 존 마크타가트가 유명하며, 공간의 관계설을 주장한 철학자로서 고트프리트 빌헬름 라이프니츠나 에른스트 마하가 알려져 있다.
- 만약 시공이 존재한다면, 그것은 실체를 가지는가?
- → 아인슈타인의 일반 상대성 이론은 시공을 실체적으로 파악하는 것과 통상을 이해할 경우 실체설(substantivism)에 서게 된다. 시공의 반실체설의 논자로는 존 아만등이 있다.
- 시공의 구조가 리만 기하학적이라는 것은 객관적인 사실인가? 그렇지 않으면 기술의 방법에 상대적 단순한 규칙인가?
- → 아이슈타인은 일반 상대성 이론의 시공이 리만 공간인 것을 객관적인 사실이라고 생각했지만, 이것을 단순한 규약이라고 생각한 철학자들도 많았다. 규약 주의를 주장한 철학자로서는 앙리 푸앵카레, 한스 라이헨바흐 등이 있다.
- 시간의 방향을 결정하는 것은 무엇인가(시간의 화살)?
- → 기본적인 물리 법칙은 모두 시간 대칭이어서, 이들에 따라서 시간의 방향은 정의할 수 없다. 열역학 제2 법칙을 이용해서 시간의 방향을 정의하는 생각, 우주의 팽창을 이용하여 시간의 방향을 정의하는 생각, 양자 역학에서의 파속의 수습을 통해 시간의 방향을 정의하는 생각 등이 제안되어왔다.
- 역방향의 인과는 가능한 일인가, 시간 여행은 가능한가?
- → 시간과 공간이 본질적으로 다르지 않은 것이 상대성 이론으로부터 나타났다. 광속을 넘어 이동하는 것으로 역방향 인과나 과거의 시간 여행도 할 수 있는 것이 아닌가 하는 가능성이 제기되었다. 하지만 시간 여행은 원리적을 불가능하다고 생각하는 논자도 있었다.[11]
마음에서의 공간[편집]
역사적으로 공간은 인간의 심적 작용이 일어나는 마음을 담고 있는 그릇과 같은 것으로 비유됐다. 이러한 의미에서 공간의 역할을 강조한 빈 공간은 문학, 심리학, 종교, 철학 등에서 마음을 적절히 표현하기 위해 다양하게 언급하거나 비유했다.[1]
가상 공간[편집]
가상 공간(假想 空間) 혹은 사이버 공간 또는 사이버스페이스(cyberspace)는 현실 세계가 아닌 컴퓨터, 인터넷 등으로 만들어진 가상의 공간을 의미한다.
- 정의
사이버스페이스라는 용어는 윌리엄 깁슨이 1984년에 쓴 과학 소설인 뉴로맨서에서 최초로 등장했다. 인공 두뇌학(cybernetics)을 뜻하는 Cyber와 공간을 뜻하는 Space의 합성어로서 현실이 아닌 두뇌 속에서 펼쳐지는 또 다른 우주를 뜻한다. 사이버스페이스라는 용어는 존 페리 발로가 의사 전달의 공간(Communication Space)이라는 개념으로 사용하면서부터 일상적인 용어가 됐다.
사이버스페이스에선 국경과 이념의 한계가 없고 지리적 위치, 시간, 신분상의 제한을 받지 않고 누구에게나 실시간 혹은 비실시간으로 정보의 선택 및 송수인 가능하다. 사이버스페이스에선 다양한 활동을 할 수 있는데, 사이버 교육은 이러한 사이버 공간 내에서 이루어지는 교육의 한 사례이다. 컴퓨터, 인터넷상의 데이터 영역을 다수의 이용자가 자유롭게 정보를 주고받는 곳이고 최근에는 컴퓨터 네트워크상에서 행해지는 범죄를 사이버 범죄라고 칭한다. 컴퓨터 네트워크상에 구성된 사회, 즉 사이버스페이스에 대한 인식이 정착되었다.[12]
스마트공간[편집]
메타버스(metaverse) 개념을 전시공간 구축에 활용한다는 것은 매우 흥미롭고 의미 있는 일이다. 메타버스에는 물리적 전시공간에 담긴 모든 콘텐츠를 담아낼 수 있다. 물리적 공간의 한계를 넘어서 제한 없이 콘텐츠를 담아낼 수 있을뿐더라 콘텐츠의 형태와 구성 방식도 전시 목적에 따라서 얼마든지 자유롭게 구축할 수 있다. 물리적 전시공간 내 매체 시스템의 작동에 의해서 원하는 사용자에게 콘텐츠로 제공된다. 메타버스 개념의 활용은 전시공간을 풍성하고 스마트하게 하는 것에 도움을 준다.[13]
인간들은 특정 목적으로 공간을 구획하고 창출하거나 파기하여 공간 내에서 사회생활을 이어간다. 인간의 모든 사회생활이 다양한 공간 속에서 다뤄지며 사회생활의 다양한 단위들이 공간을 통해 특징적으로 개념 지어지기도 한다. 사회생활의 많은 부분이 공간을 매개로 이루어지고 있다. 공간 개념은 세계, 대륙, 영토, 지역, 국가 등 상대적으로 추상성 높은 공간과 주택, 방, 극장처럼 물리적 특성이 구체적인 공간을 모두 포함한다. 전시공간은 근대 이후 성립된 종합 박물관(Museum)과 근대 이후 분화 발전해 온 미술관(Museum of Art), 과학관(Museum of Science) 등의 특화 박물관, 세계박람회(EXPO)와 여기서 분화된 테마파크, 전시 컨벤션 등을 포괄한다. 사람들은 정보 획득, 학습, 오락 등을 목적으로 전시공간을 방문하여 관람하고 체험하는 공간적 실천을 하고 있다. 전시공간은 전시를 주관하는 주체의 공간적 실천을 통해 생성되며, 대중들의 다양한 목적의 공간적 실천을 통해 활용되는 두 가지 공간적 실천이 중첩되는 문화영역이다.[13]
유비쿼터스 환경[편집]
전시공간을 포함한 문화공간을 제3의 공간으로 분류하는 기준이 있다. 인간이 만든 사회적 공간 중 제1의 공간(the first space)을 주거공간으로 제2의 공간(thesecond space)을 일하는 공간으로 했다. 1980년대 들어 제1의 공간도 아니고 제2의 공간도 아닌데 감각적으로 짜릿하고 집처럼 편안한 문화공간에 대한 대중들의 수요가 발생하면서 조성되는 이러한 문화공간을 제3의 공간(the third space)으로 분류했다. 제4의 공간(4D space)이란 개념의 논의도 있다. 공간의 진화 방향을 예측한 제4의 공간은 디지털 기술의 발달 이후 인간의 행동에 반응하는 공간(responsiveenvironments)에 대한 새로운 개념이다.
조성되는 건축에 마치 하나의 구조물처럼 인터랙티브 디지털 매체가 설치되어 있음으로 인간의 행동에 반응하는 공간이 생성된다. 이러한 공간환경은 전시공간 구축에서 최근 많이 활용되고 있다. 이러한 공간은 특히 첨단기술을 활용하는 세계박람회의 전시공간에서 많이 활용된다. 공간에서 인간 행동이나 인터랙티브 작동행위를 감지하고, 이에 따라 공간의 분위기가 달라지거나, 특정 퍼포먼스가 일어나거나, 특정 정보가 제공되는 등의 반응이 일어나는 시스템이다. 미디어 월(mediawall), 인터랙티브 플로어(interactive floor), 미디어 테이블(media table) 등의 개념이 인터랙티브 공간을 형성하는 매체들이고 그 밖에도 다양한 센싱 기술과 유무선 네트워크 기술을 디지털 전시 매체와 조합하고 시스템화하면 다양한 인터랙티브 콘텐츠를 구현할 수 있다. 이러한 공간을 위해서는 유비쿼터스(ubiquitous) 환경이 필요하다. 공간에 머무는 사람이 어느 장소에서나 네트워크 컴퓨터를 의식하지 않고 자유롭게 접속할 수 있는 정보통신 환경이 필요하다. 공간은 다양한 인터랙티브 매체가 적절하게 배치되어 있으며, 이 매체들은 유비쿼터스 환경에서 유무선 네트워크로 콘텐츠 아카이브나 데이터베이스 등에 연결되어 사용자의 인터랙티브 행위에 따라 서비스 시스템이 통제됨으로 특정 콘텐츠를 제공하는 반응이 일어나는 공간이 진정한 제4의 공간이라고 할 수 있다.
최근 전시공간은 제4의 공간으로 가는 중요한 과정이다. 이러한 진보가 이루어진 68 전자통신 동향분석 제29권 제3호 2014년 6월다면, 수용자 대상에 따른 맞춤형 정보 제공이 가능해지고 체험 전시요소가 강화되며, 실감형 콘텐츠 구현도 자유로워질 수 있는 변화가 이루어질 수 있다. 더불어 전시공간에서는 개인화된 스마트 디바이스 활용과 관련된 기술개발도 활발히 이루어지고 있다. 유비쿼터스 환경 하의 전시공간에서 인터랙티브 매체와 디지털 아카이브의 연동, 그리고 개인화된 스마트 디바이스를 활용한 다양한 콘텐츠 서비스까지 가능할 수 있을 것으로 본다. 근대에서 시작된 전시공간은 변화를 계속해 왔고 현재도 어느 때보다도 빠른 속도로 변화하고 있다.[13]
스마트공간 개념[편집]
공간디자인의 관점 : 유비쿼터스 기술로 진화되는 공간 환경에서 기존의 공간디자인에서 추구해온 다양한 가치(예를 들면 인간 중심의 공간구성과 동선체계, 심미성, 친환경성 등)를 유지하거나 확대 발전시킬 방안에 대한 논의를 위한 것이다. 이러한 이유로 공간디자인 분야에서의 스마트공간에 대한 연구와 논의는 스마트공간의 특성을 도출하고 스마트공간에서 새로운 디자인 방안을 연구하고 제시하는 논의들이 주를 이루고 있다.
정보통신기술 분야의 관점 : 스마트공간은 기존의 유비쿼터스 컴퓨팅이 적극적으로 구현된 물리적 공간 정도로 보고 있다. 스마트공간이란 개념 자체의 유용성에 별다른 관심이 없다. 하지만 정보통신기술이 추구하는 유비쿼터스 공간 환경이 인간 생활에 유용한 스마트공간으로 구현되기 위해서는 큰 노력이 필요하다. 유비쿼터스 컴퓨팅으로 구축된 공간에서 사용자인 인간의 편리를 증진하게 시키기 위해선 유비쿼터스 환경에서 콘텐츠 제작 및 서비스 관련 기술이 함께 연구되고 개발돼야 한다. 유비쿼터스는 물리적 공간의 기술환경이고 이를 통해 스마트공간이 완성되기 위해서는 환경에 맞는 콘텐츠 제작, 구축 및 서비스 기술이 필요하다.
공간디자인 연구 분야에서 꾸준히 연구해 온 스마트공간에 대한 논의 성과도 충분히 받아들여 연구에 활용해야 완성도 높은 스마트공간 구현이 현실성 있게 이루어진다. 스마트공간 기술은 유비쿼터스 컴퓨팅 기술과 유비쿼터스 환경하에서의 디지털콘텐츠 제작 구축 서비스 기술, 그리고 유비쿼터스 환경에 따른 공간디자인 기술이 융합되어 이루어지는 기술이다. 스마트공간이란 지능형 환경을 제공하기 위해 물리적 공간을 구성하는 요소를 컴퓨팅 화하고 네트워킹 화하여, 공간에 있는 사람과 사물들이 그 공간과 전자적으로 소통하는 것을 의미한다. 공간 자체의 인지 상황 정보에 따른 편의 제공과 함께, 떨어진 공간이라도 인지적, 감각적으로 연결되어 유기체적인 관점으로 구성된 공간이다. 스마트공간은 그 물리 공간을 구성하는 전자적 장치가 아니라 물리공간 내 사용자의 가치관, 취향, 상황 목적에 따른 행위에 따라 반응하는 공간(responsiveenvironments)으로 인간적인 요소가 포함된 개념이고 최적의 편의성을 추구하여 사용자에 제공되는 다양한 콘텐츠와 서비스 시스템까지 포함한다.[13]
전시기술의 트렌드와 스마트공간[편집]
현대 전시공간은 디지털 기술을 어떤 문화산업 분야보다 빠르게 수용하고 있다. 이러한 전시공간의 첨단 기술 수용은 새로운 것을 추구하는 전시문화의 원형적 특성이 한 원인이다. 지금은 영화와 텔레비전에서 상용화되어 있는 쓰리디 입체영화도 전시산업에서 시작되었고, 라이드 필름(ride simulation film), 아이맥스 영화(Imax Large Format film), 포디 영화(4D attractionfilm) 같은 새로운 영상 기술을 적용한 콘텐츠들이 모두 전시공간에서 우선으로 구현됐다. 이런 콘텐츠 기술은 90년대 디지털 기술의 획기적 발전을 통해 진화를 거듭하고 현재는 전시 분야뿐 아니라, 보편적인 문화기술(culture technology)이 되었다. 또한 정보검색 분야에서도 터치 기반의 키오스크(kiosk)부터, 탈중앙화 신원증명(DigitalInformation Desk, DID), 미디어 테이블(media table) 등으로 발전되었다. 데이터의 기기저장 방식에서 아카이브 연동방식으로까지 진화되고 있다. 새로운 정보통신기술을 가장 먼저 적용하는 산업부문 중 하나가 전시 분야이다. 최근의 전시공간 구축의 주요 트렌드를 보여준다.
최근 전시공간은 물리적인 공간을 뛰어넘어 가상공간으로 확장 시켜나가고 있다. 가상현실(VirtuaReality, VR)기술, 증강현실(Augmented Reality, AR)기술, 홀로그램(hologram) 기술, 사이버(cyber) 전시기술 등은 물리적으로 제한된 전시공간에서 차원이 다른 무한의 공간을 창출하고, 현실에서는 경험할 수 없는 초현실적 공간을 연출할 수 있다. 최근 전시공간 구축의 또 다른 기술 트렌드는 이용자 체험성의 강화다. 체험 전시 매체의 발달은 인간의 감각을 확장하는 방향으로 이루어진다. 감각을 확장한다는 것은 두 가지 의미가 있다. 첫째, 특정 감각에 대한 자극을 강하게 한다는 의미와 둘째, 다 감각을 동시적으로 자극한다는 의미이다. 기존 미디어에선 경험할 수 없었던 체험전시에 대한 요구와 오감을 활용하는 실감 콘텐츠에 대한 요구가 전시공간에서의 다 감각 매체 개발과 도입을 지속해서 추구하게 만든다. 또한 최근 전시공간에서는 스마트 디바이스를 활용하는 자동안내 시스템이 확대되고 있고 디지털 아카이브 서비스는 실물 오브제 전시공간에서 정보검색 서비스를 담당하여 아카이브 서비스 룸을 확장하고, 웹과 앱에서 아카이브 검색 서비스를 제공하는 방식으로 확대되고 있다.
디지털 기술은 기존의 전시 매체를 획기적으로 개선해 실물전시 위주의 전시공간을 디지털 매체가 중심인 공간으로 변화하고 있다. 유물 없는 박물관을 가능하게 하고 있고 실물 위주의 기존 아날로그 전시방식을 디지로그(Digilog) 전시나 아나탈(Anatal) 전시라는 새로운 개념의 전시 형태로 전이시키고 있다. 이러한 전시공간 구축기술의 발달은 스마트전시를 지향하고 있다. 스마트공간 구현에 필요한 유비쿼터스 컴퓨팅을 지향하고 있으며(다양한 센싱 기술과 인터랙티브 기술 및 스마트 디바이스 활용기술 등), 디지털 콘텐츠 서비스 기술의 진화도 향상되고 있다. 데이터 연동 콘텐츠 서비스 기술은 이용자 맞춤형 서비스를 가능하게 하고(맞춤형 서비스, 추천기술 및 데이터 마이닝 기술 등) 체험성이 높은 콘텐츠 기술은 다양한 실감 콘텐츠 서비스를 체험할 수 있게 했다. 특히 시공간 압축을 위한 다양한 가상 콘텐츠 제작 및 서비스 기술 확장은 물리적 공간을 초월한 스마트 전시공간을 지향하는 최근 전시문화의 지향점을 명확히 알 수 있는 지점이다.[13]
스마트전시와 메타버스 서비스[편집]
메타버스(metaverse)는 메타(meta) + 유니버스(universe)를 합친 의미로 우주와 또 다른 차원의 우주, 즉 공간 개념으로 보면 현실공간과 또 다른 가상의 공간 세계를 칭하는 개념이다. '메타버스는 융합이다. 메타버스는 가상적으로 확장된 물리적 현실과 물리적으로 영구화된 가상공간의 융합이다. 그리고 이용자가 그것을 경험할 때는 동시에 혼재돼서 나타난다'고 정의되고 있다. 3차원 가상공간에 현실을 더함으로써 그 범위를 적극적으로 확장시키고 있는 것이다. 메타버스는 우리의 가상공간과 현실이 적극적으로 상호작용하는 공간이다. 메타버스는 현실과 가상세계의 교차점이 쓰리디 기술로 구현된 또 하나의 세계를 가리킨다.
스마트 전시공간에서 메타버스의 구현과 활용은 디지털 콘텐츠 기술 분야의 확장으로 의미를 가진다. 전시공간에서 전시되고 있는 실물 오브제가 디지털 복제를 통해 가상의 쓰리디 그래픽 이미지로 대체될 수 있는 차원을 넘어서 특정 공간을 메타버스로 구현한다면 그 공간은 수많은 오브제와 관련 콘텐츠를 담아낼 수 있는 획기적인 메타콘텐츠(metacontents)가 될 수 있을 것이다. 메타버스는 전시공간과 관련한 고도의 추상 세계인 버추얼 세계(virtual world)가 될 수 있고 전시공간을 그대로 복제한 거울 세계(mirror world)가 될 수도 있다. 그리고 두 메타버스 사이에 다양한 추상성 층위의 융합 개념 메타버스가 구현가능할 것이다. 이를 토대로 전시공간에서 메타버스의 활용은 전시공간의 확장은 물론 전시 아이템의 무한한 확장을 가능하게 한다. 메타버스 개발 및 서비스 기술은 스마트 전시공간의 콘텐츠 기술에 중요한 요소가 된다. 예를 들어 하나의 전시 오브제인 공룡의 뼈 화석으로부터 그 공룡이 살고 있었던 수백만 년 전 세계를 메타버스로 구현하여 화석이 된 공룡과 관련 이야기를 콘텐츠화해 메타버스 서비스를 할 수 있다. 이러한 콘텐츠 장르로는 팩션(faction)이 될 것이며 메타버스는 버추얼(virtual) 공간이 될 것이다.
메타버스의 구현은 쓰리디 그래픽을 활용한 리얼리티 구현이 기본적인 개념이라고 할 수 있다. 하지만 전시 목적과 환경에 따라 다양한 수준의 구현기술 적용이 가능하다. 또한 이 메타버스에 대한 서비스 형태도 서비스 기술에 따라 다양한 수준에서 이루어진다. 먼저 메타버스에 아바타를 전송 시켜 플레이하는 가상체험 형식의 서비스가 메타버스의 기본적인 서비스 형태나, 과도기적인 현황에서 메타버스 콘텐츠를 단순히 선택적 관람을 하는 방식으로 콘텐츠 서비스가 제한될 수도 있다. 콘텐츠 서비스 기술은 전시 매체 관련 기술, 서비스 장치, 전시공간의 통신환경 등 다양한 환경 조건에 따라 결정된다.[13]
- 유사 사례
- 베를린 자연사 박물관(Museum für Naturkunde)
메타버스 기반 스마트 전시 안내 시스템 개발[편집]
방문객이 즐겁게 전시공간을 관람하게 하기 위해서 입장 전에 관람객 머릿속에 전시공간의 맵을 인지시켜야 한다. 움직이는 동선에 대한 불안감 없이 공간을 관람할 때 집중도가 높아지고 효율적인 관람이 이루어질 수 있다. 그래서 방문객들은 어김없이 입구에서 전시공간의 맵을 찾는다. 그런데 공간이 넓거나 실내와 실외 공간을 오가는 복잡한 구조의 공간이라면 단순히 방문객에게 맵을 주는 것으로는 부족하다. 메타버스 기반 스마트 전시 안내 시스템 개발 과제는 전시공간의 메타버스 - 거울 세계를 구축하고 방문객들이 메타버스에서 아바타 가상투어를 하도록 유도한다. 이를 통하여 방문객들 머릿속에 공간의 맵을 인지 시켜 실제 공간에 나아가도록 하기 위한 서비스 기획이다. 또한 이용자의 체험성을 높이고 엔터테인먼트 요소를 강화하기 위한 기획이기도 하다.[13]
- 시스템 특징
- 중대형 실내형 전시공간, 야외형 전시공간, 전주 한옥마을과 같은 곳에 가이드 시스템으로 활용 가능한 서비스와 황룡사, 미륵사지와 같은 사라진 문화 유적지에 대한 가상공간 복원 및 가상투어를 통한 전시 가이드 시스템으로 활용도가 높을 것으로 기대한다.
- 스마트 디바이스 앱과 전시 미디어가 연동하는 전시 안내 시스템으로 모바일과 위치 기반 미디어 특성을 연동하는 다양한 서비스 시나리오를 구현하는 기술
- 개인의 스마트 디바이스에서 생성한 아바타를 전시 미디어에 포팅(porting)하고 컨트롤하여 인터랙티브 방식의 전시 안내 서비스를 받는 기술
- 전시 미디어에 전시공간 전체 맵이 쓰리디 기반의 메타버스로 구현되고, 관람자가 앱에서 생성한 자신의 아바타를 전시 미디어로 전송하고 메타버스를 가상 투어하여 필요한 정보와 아이템들을 획득해 자신의 스마트 디바이스에 받음.
- 메타버스 가상투어는 동시에 다수의 이용자(현재 40명 동시접근 구현)가 참여할 수 있고 참여자들은 서로 실시간 채팅 형식의 대화를 나눌 수 있다.
- 실제 전시공간에 앱을 활성화한 채 관람을 하는 이용자는 자신의 위치에서 생성한 콘텐츠(사진, 텍스트 등)를 올릴 수 있고 업로드된 콘텐츠는 메타버스 내 같은 위치에 누적되며, 업로드 정보가 메타버스 내 위치에 남는다.
- 개발 예정
현대의 전시산업은 근대 생성 이후 첨단기술을 가장 빠르게 수용하여 전시공간을 구축과 운영하며 발전시켜왔다. 1990년대 이후 정보통신기술의 급속한 발전은 전시공간을 유비쿼터스 컴퓨팅 환경과 다양한 디지털 콘텐츠 구현 및 서비스 기술의 상호적 발전과 더불어 전시공간의 스마트공간 화를 가능하도록 했다. 전시공간에서 메타버스 개념의 적용은 전시공간의 물리적 한계를 넘어서는 획기적인 전시 방법의 대안이 될 수 있으며, 전시공간을 스마트공간으로 확장하는 중요한 분야임을 알았다. 미래부 과제로 진행되는 메타버스 기반 스마트 전시 안내 시스템개발에서 스마트 디바이스 - 전시 미디어 연동 시스템(MMOID)을 활용한 메타버스 가상체험 전시안내 시스템개발은 현재의 전시공간 기술 수준을 향상할 수 있는 잠재적 외연이 넓은 기술개발 과제임을 숙지하길 바란다. [13]
자동차 실내 공간[편집]
- 헤드룸 : 탑승자가 시트에 착석한 상태에서 머리 위 공간을 가늠할 수 있는 수치를 의미한다. 시트의 힙 포인트에서 헤드라이닝까지의 거리를 측정해 표기한다. 미국자동차공학회(SAE) 기준으로는 힙포인트에서 헤드라이닝까지의 측정값에 102mm(4인치)를 더한 수치를 발표치로 한다.
- 숄더룸 : 탑승자가 시트에 앉았을 때 어깨 공간을 확인할 수 있는 수치다. 좌측 도어 트림부터 우측 도어 트림의 상부(팔거치부 위쪽)간 최소 수평거리를 측정해 표기한다. 실제 승차 시 너비 공간을 가늠할 수 있다. 주로 도어트림 상부 형상에 따라 수치가 달라진다.
- 레그룸 : 탑승자의 다리 여유 공간을 나타낸 수치로, 실내 공간 크기 수준을 가늠할 수 있는 주요 수치로 여겨진다. 보통 시트의 힙 포인트부터 발을 최대한 뻗을 수 있는 곳까지의 수치를 측정해 표기한다. 미국자동차공학회(SAE) 기준으로는 힙포인트에서 발목까지의 측정값에 254mm(10인치)를 더한 수치를 발표치로 한다
- 풋룸 : 일반적으로 승객의 발을 두는 공간을 의미한다. 전석 보다는 후석의 풋룸을 중요시 하는데, 2열의 풋룸은 1열 시트 하단부 구조물에 의해 좌우폭과 높이에 따른 공간이 결정되며 시트 하부에 발을 뻗을 수 있는 정도에 영향을 주기 때문에 후석 레그룸에 영향을 준다.
각주[편집]
- ↑ 1.0 1.1 1.2 1.3 1.4 1.5 〈공간〉, 《위키백과》
- ↑ 2.0 2.1 2.2 〈공간〉, 《나무위키》
- ↑ 3.0 3.1 3.2 3.3 3.4 3.5 3.6 3.7 〈공간〉, 《네이버 지식백과(현상학 사전)》
- ↑ 〈바나흐 공간〉, 《위키백과》
- ↑ 〈유클리드 공간〉, 《위키백과》
- ↑ 〈거리 공간〉, 《위키백과》
- ↑ 〈벡터 공간〉, 《위키백과》
- ↑ 〈사영 공간〉, 《위키백과》
- ↑ 〈위상 공간〉, 《위키백과》
- ↑ 〈확률 공간〉, 《위키백과》
- ↑ 〈시간과 공간의 철학〉, 《위키백과》
- ↑ 〈가상 공간〉, 《위키백과》
- ↑ 13.0 13.1 13.2 13.3 13.4 13.5 13.6 13.7 13.8 13.9 김성희·이현우·류원·김광신, 〈스마트공간과 메타버스 전시안내 기술개발 동향〉, 《전자통신동향분석 제29권 제3호》, 2014-06
참고자료[편집]
- 〈공간〉, 《위키백과》
- 〈공간〉, 《나무위키》
- 〈공간〉, 《네이버 지식백과(현상학 사전)》
- 〈바나흐 공간〉, 《위키백과》
- 〈유클리드 공간〉, 《위키백과》
- 〈거리 공간〉, 《위키백과》
- 〈힐베르트 공간〉, 《위키백과》
- 〈벡터 공간〉, 《위키백과》
- 〈사영 공간〉, 《위키백과》
- 〈위상 공간〉, 《위키백과》
- 〈확률 공간〉, 《위키백과》
- 〈시간과 공간의 철학〉, 《위키백과》
- 〈가상 공간〉, 《위키백과》
- 김성희·이현우·류원·김광신, 〈스마트공간과 메타버스 전시안내 기술개발 동향〉, 《전자통신동향분석 제29권 제3호》, 2014-06
같이 보기[편집]
| ||||||||||||||||||||||||||||||

 위키원
위키원






















































![{\displaystyle \mathbb {P} _{\mathbb {Z} }^{n}=\operatorname {Proj} \mathbb {Z} [x_{0},x_{1},\dots ,x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32be7178b44690b7f9cd70c6392421006ff1ddd6)
![{\displaystyle \mathbb {Z} [x_{0},x_{1},\dots ,x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae407b84b2db705344fd13c4d7aede6dbf2487f7)





![{\displaystyle \mathbb {P} _{\operatorname {Spec} R}^{n}=\operatorname {Proj} R[x_{0},x_{1},\dotsc ,x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/29d78243ed206e08a2797dd29ab18e1ec0425c7f)