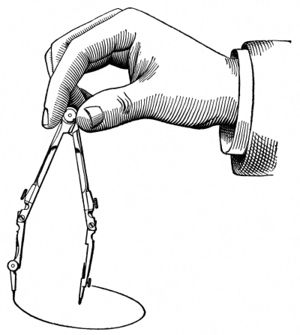
컴파스
컴파스(compass)는 원 등을 작도할 때에 쓰는 기구다. 그리려는 원이나 호의 크기에 맞춰 두 다리를 벌리고 오므려 사용한다.
컴퍼스는 보통 금속이나 플라스틱으로 만들어져 있으며, 힌지로 연결된 두 부분을 이루는데, 이 힌지는 그려지는 원의 각을 변경할 수 있게 되어있다. 일반적으로 한 부분은 끝에 뾰족한 부분이 있고 다른 한 쪽은 연필이나 펜으로 되어있다.
순우리말은 걸음쇠, 한자로는 양각규(兩脚規)이다.
개요[편집]
원 또는 원호를 그릴 때 쓰는 기구.
연필용과 먹물용이 있으며 크기는 큰 것, 중간 것, 작은 것 등이 있다. 큰 컴퍼스는 반지름 70∼130㎜인 원이나 호를 그릴 때 쓰고, 중간 컴퍼스는 반지름 50∼70㎜인 것, 스프링 컴퍼스는 반지름 50㎜ 이하의 것을 그릴 때 쓰며 디바이더용·연필용·샤프용·먹줄펜용이 있다. 그밖에 아주 작은 원을 그릴 때는 드롭 컴퍼스를 쓴다.
큰 컴퍼스는 보통 두 다리가 바늘 끝으로 되어 있으나, 한쪽 다리는 연필이나 먹줄펜을 갈아 끼울 수 있도록 되어 있다. 사용할 때는 연필심을 바늘 끝보다 0.5㎜ 정도 짧게 하여 바늘이 뜨지 않도록 하고, 연필심은 쐐기 또는 끌 모양으로 납작하게 갈아 그리는 선이 굵어지지 않게 한다. 작은 원과 호는 컴퍼스의 다리를 곧게 펴서 그리고, 큰 원과 호는 다리를 제도용지에 수직으로 구부려서 그린다. 아주 큰 원이나 호는 컴퍼스에 이음대를 끼워서 그린다. 중간 컴퍼스로 원을 그릴 때는 원의 중심이 되는 다리를 구부리지 않는 것이 좋다.
설명[편집]
종류와 크기가 여러 가지며, 한쪽은 날카로운 송곳으로 되어 있고 다른 한 쪽은 연필 등의 필기구를 끼워 쓸 수 있도록 되어 있는 것이 공통점이다. 연필심이나 샤프같은 필기구 대신 먹물을 집어넣어 쓰는 먹줄펜(오구)가 달린 경우도 있다. 또, 다른 한 쪽까지 바늘로 되어 있는 즉, 양쪽 모두 송곳으로 되어있는 것은 디바이더라고 한다. 사용법으로는 필기구를 단단히 연결한 다음 그리고자 하는 반지름을 자 등을 이용하여 맞추고, 송곳을 원의 중심에 놓은 뒤 한 바퀴 돌려 주면 원이 그려진다.
제도기의 구성 도구 중 하나다.
고대 그리스 시절에 '작도'라고 하면 눈금이 없는 자와 컴퍼스만을 이용하여 도형을 그리는 것을 의미했다. 여기서 유래된 수학 문제가 많은데 대표적인 예가 3대 작도 불능 문제.
제도기의 구성도구이기도 하고, 고대 공학과 수학에서 부터 있었던 유서깊은 도구인 탓에 컴퍼스는 공학의 상징으로 자주 쓰인다.
학교 앞 문구점에서 흔히 파는 싸구려 컴퍼스는 두 다리와 이를 끝에서 연결하는 나사만으로 되어 있으며, 약간 뻑뻑하게 두 다리를 넓히고 좁힐 수 있도록 되어 있다. 이런 종류의 컴퍼스는 원을 그리다가 다리가 움직여 삐끗하는 경우가 많아 불편하다. 그래서 약간 비싼 컴퍼스는 두 다리 사이의 간격을 조절하는 데 쓰는 긴 나사가 중간에 끼워져 있다.
이 물건이 급히 필요한데 구할 수 없다면, 간단히 간이 컴퍼스를 제작할 수 있는데 적당히 빳빳한 종이를 가늘고 길게 잘라 한쪽에 작은 구멍을 꿇어 샤프 등으로 고정한 후 적절한 거리에 또 하나의 구멍을 뚫어 샤프 등을 꽂아 한 쪽을 고정하고 반대쪽 샤프를 잡고 잘 돌리면 적절한 원이 그려진다.
독일민주공화국의 국기에 존재하는데, 동독 국기의 컴퍼스는 지식인을 상징한다.
프리메이슨의 상징 문양에도 등장하는데, 건축가 집단에서 유래했다고 주장하는 이들의 특성 상, 제도에 사용되는 도구를 그려놓은 것. 정확히는 디바이더지만...
위험성[편집]
침(針)이 매우 날카로워서 베이거나 찔릴 수 있기 때문에 주의해야 한다. 특히 학교에서는 컴퍼스를 학생들에게 각자 지참 및 관리하게 하는 경우가 많은데, 컴퍼스 침이 흉기로 악용될 수 있기 때문에 컴퍼스가 필요한 수업시간마다 1인 1개씩만 지급하고 수업 후 반납하도록 하는 것이 바람직하다. 성인들이 수용되어 있는 교도소에서도 금속제 수저가 흉기로 악용될 수 있기 때문에 플라스틱제 수저를 지급하는데, 미성년자들이 많은 학교에서 수저보다 매우 날카로운 컴퍼스를 학생에게 직접 지참하게 하는 것이야말로 고양이에게 생선가게 맡기는 꼴이다.
갈릴레오의 컴퍼스[편집]
갈릴레오의 컴퍼스(Galileos' compass)는 갈릴레오 갈릴레이가 수학적 계산과 기하학적 계산을 편리하게 할 수 있도록 만든 컴퍼스의 하나이다.
갈릴레오의 컴퍼스는 무기술이 발달하면서, 더욱 더 정밀한 수학적 계산을 요하는 르네상스시대때 만들어졌다. 이때 갈릴레오의 컴퍼스와 함께 비례컴퍼스가 발전됐다. 1597년도 파두아에서 발명되었고, 델리 아카데미에서 갈릴레오의 활약과도 관련이 있다. 17, 18세기에 발전되어 오다가 19세기에 와서 비례 컴퍼스는 점차 정밀한 슬라이드 룰러로 대체되었는데, 최근의 컴퓨터가 나올 때까지 여러 공학자, 기하학자와 건축학자들이 사용했다.
구성 및 용도[편집]
갈릴레오 컴퍼스는 두 개의 서로 맞물려 돌아갈 수 있는 자와 두 자 사이에 연결되어 있는 쿼드란트로 이루어져 있다. 비례선은 총 7개의 종류가 있으며, 쿼드란트는 총 4개의 스케일이 있다. 각각의 비례선은 수리선(The Arithmetic Lines), 기하선(The Geometric Lines), 입방선(The Stereometric Lines), 측정선(The Metallic Lines), 다면체선(The Polygraphic Lines), 다각형선(The Tetragonic Lines), 추가선(The Added Lines)으로 불린다. 각각의 쿼드란트는 차례대로 첫째(first), 둘째(second), 셋째(third), 넷째(fourth) 스케일(scale)이라고 불린다. 이 컴퍼스의 다리에 새겨진 일곱 개의 비례선과 쿼트란드에 표시되어 있는 네 개의 스케일들은 이자율계산, 제곱근과 세제곱근을 계산하고, 면적이나 체적을 구하는 데에까지 다양하다.
비례선[편집]
- 수리선 : 250개의 같은 부분으로 등분하는 축척으로 덧셈, 뺄셈, 곱셈, 나눗셈을 할 때에 쓰인다.
- 기하선 : 넓이가 각각 1, 2,······,50인 정사각형의 각 변의 길이의 비율을 나타내는 축척으로 컴퍼스의 중심으로부터의 각 점까지의 거리가 1, √2, √3,······, √50과 같다. 주로 제곱근을 구하는 데에 사용된다.
- 입방선 : 부피가 각각 1, 2, ······, 140인 정육면체의 각 모서리의 길이의 비율을 나타내는 축척으로 컴퍼스의 중심으로부터의 각 점까지의 거리가 1,∛2, ∛3,······,∛140과 같다. 주로 세제곱근을 구하는 데에 사용된다.
- 측정선 : 같은 무게를 가지는 금, 납, 은, 구리, 철, 주석, 대리석 등의 서로 다른 금속으로 이루어진 구의 지름의 비율을 나타내는 축척이다. 이 선은 포병들이 미사일의 직경을 계산하는 데에 사용되었다.
- 다면체선 : 변의 길이가 모두 같은 변이 3개인 것부터 15개인 정다각형들의 외접원의 반지름의 비율을 나타내는 축척이다. 이 선을 이용해서 정다각형을 그릴 수 있고 원을 똑같은 부분으로 나눌 수도 있다.
- 다각형선 : 넓이가 똑같은 변이 3개인 것부터 13개인 정다각형의 각 변의 길이의 비율을 나타내는 축척이다. 정다각형의 넓이를 구하는 데에 사용된다.
- 추가선 : 같은 길이의 현을 가지는 20개의 부채꼴의 지름을 나타내는 바깥쪽에 새겨진 축척과 각 부채꼴과 같은 넓이를 가지는 정사각형의 각 변의 길이를 나타내는 안쪽에 새겨진 축척으로 이루어져 있다. 이 선은 부채꼴의 넓이를 구하는 데에 사용된다.
쿼드란트[편집]
- 첫째 스케일(Gunner' square) : 포탄 발사대인 대포의 정밀한 발사각도를 구하는데 사용된다.
- 둘째 스케일(Astronomical quadrant) : 바다위의 움직이는 배에서 쓰이는 쿼드란트로, 배 위에서 천체를 관측할 때 보고 있는 별이 수평선으로부터 몇도만큼 천구에 위치해 있는지 알아볼 때 사용된다
- 셋째 스케일(Scale of slopes) : 어떤 건축물이나 벽의 기울기를 측정하는데 쓰인다.
- 넷째 스케일(Shadow square) : 직접 재기 어려운 높은 건축물이나 산의 높이를 재거나 멀리 떨어진 두 장소 사이의 거리를 구하는데 쓰인다.
참고자료[편집]
같이 보기[편집]

 위키원
위키원