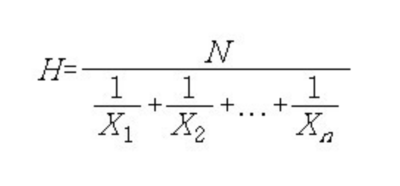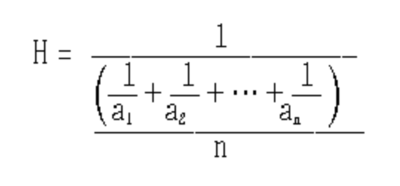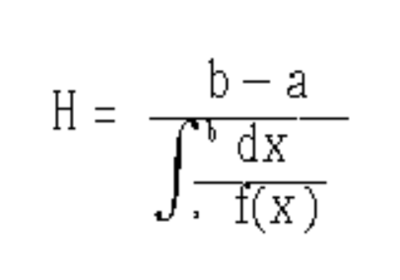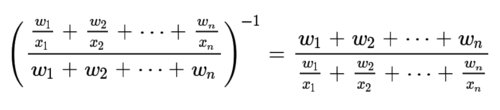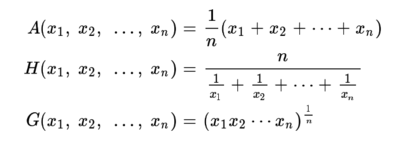"조화평균"의 두 판 사이의 차이
(새 문서: '''조화평균'''<!--조화 평균-->(調和平均)은 주어진 수의 역수의 산술평균을 구한 것의 역수를 말한다. == 개요 == 조화평균은 주어진 집...) |
잔글 |
||
| 4번째 줄: | 4번째 줄: | ||
조화평균은 주어진 집단의 측정결과에 대한 대표치의 하나로서 개별점수의 역(速)의 산술평균의 역(速)을 말한다. 각 개인별 측정치를 X1, X2, ...Xn이 라고 하고 전체 사례수를 N, 그리고 조화평균을 H라고 하면 다음과 같이 계산된다. 조화평균은 특별한 유형의 대표치로서 그 사용이 상당히 제한되어 있다. 그러나 어떤 특정한 자료를 요약하는 데 대표치로서 다른 대표치보다 우수하고 대표치로서 오차를 피할 수 있게 해준다. 예를 들면 시간비율의 평균 또는 특정한 물가계산에 적합하다. 또 통계에 있어서 평균의 표준오차는 사례수 N에 역비례하므로 평균의 표준오차의 통합에도 사용된다. 일반적으로 조화평균은 산술평균이 갖는 편견성(偏見性)에 역(速)으로 관계되고 있다. 경우에 따라서 조화 평균이 정확한 평균치를 돌려준다. 예를 들어, 전체 거리의 절반을 40km/h의 속도로 달리고, 남은 절반을 60km/h로 달렸다면, 평균 속력은 40과 60의 조화 평균인 48km/h가 된다. 이동하는데 전체 거리를 48 km/h의 속력으로 달린 경우와 같은 시간이 걸렸기 때문이다. (만약 전체 "시간"의 절반씩을 달렸다면, 평균 속력은 산술 평균인 50km/h가 된다.)<ref>〈[https://terms.naver.com/entry.naver?docId=512201&cid=42126&categoryId=42126 조화평균]〉, 《교육학용어사전》</ref><ref>〈[https://ko.wikipedia.org/wiki/%EC%A1%B0%ED%99%94_%ED%8F%89%EA%B7%A0 조화 평균]〉, 《위키백과》</ref> | 조화평균은 주어진 집단의 측정결과에 대한 대표치의 하나로서 개별점수의 역(速)의 산술평균의 역(速)을 말한다. 각 개인별 측정치를 X1, X2, ...Xn이 라고 하고 전체 사례수를 N, 그리고 조화평균을 H라고 하면 다음과 같이 계산된다. 조화평균은 특별한 유형의 대표치로서 그 사용이 상당히 제한되어 있다. 그러나 어떤 특정한 자료를 요약하는 데 대표치로서 다른 대표치보다 우수하고 대표치로서 오차를 피할 수 있게 해준다. 예를 들면 시간비율의 평균 또는 특정한 물가계산에 적합하다. 또 통계에 있어서 평균의 표준오차는 사례수 N에 역비례하므로 평균의 표준오차의 통합에도 사용된다. 일반적으로 조화평균은 산술평균이 갖는 편견성(偏見性)에 역(速)으로 관계되고 있다. 경우에 따라서 조화 평균이 정확한 평균치를 돌려준다. 예를 들어, 전체 거리의 절반을 40km/h의 속도로 달리고, 남은 절반을 60km/h로 달렸다면, 평균 속력은 40과 60의 조화 평균인 48km/h가 된다. 이동하는데 전체 거리를 48 km/h의 속력으로 달린 경우와 같은 시간이 걸렸기 때문이다. (만약 전체 "시간"의 절반씩을 달렸다면, 평균 속력은 산술 평균인 50km/h가 된다.)<ref>〈[https://terms.naver.com/entry.naver?docId=512201&cid=42126&categoryId=42126 조화평균]〉, 《교육학용어사전》</ref><ref>〈[https://ko.wikipedia.org/wiki/%EC%A1%B0%ED%99%94_%ED%8F%89%EA%B7%A0 조화 평균]〉, 《위키백과》</ref> | ||
| − | [[파일:조화평균 계산공식1.png|썸네일| | + | [[파일:조화평균 계산공식1.png|썸네일|400픽셀|가운데|조화평균 계산공식 1]] |
n개의 양수에 대하여 그 역수들을 산술평균한 것의 역수를 조화평균이라 한다. 예를 들어, 두 지점 A, B를 갈 때는 'a' km/h의 속도로, 올 때는 'b' km/h의 속도로 왕복했다면 이 사람의 평균속력은 a와 b의 조화평균에 해당된다. 또 100m를 3회 뛴 속력이 a,b,c일 때, 평균속력은 조화평균으로 구해진다. 이와 같이 일이나 능률의 예에서는 산술평균을 구하면 틀리게 된다. | n개의 양수에 대하여 그 역수들을 산술평균한 것의 역수를 조화평균이라 한다. 예를 들어, 두 지점 A, B를 갈 때는 'a' km/h의 속도로, 올 때는 'b' km/h의 속도로 왕복했다면 이 사람의 평균속력은 a와 b의 조화평균에 해당된다. 또 100m를 3회 뛴 속력이 a,b,c일 때, 평균속력은 조화평균으로 구해진다. 이와 같이 일이나 능률의 예에서는 산술평균을 구하면 틀리게 된다. | ||
| 10번째 줄: | 10번째 줄: | ||
n개의 양수 a1, a2,…,an에 대하여 그 역수 1/a1, 1/a2, …, 1/an을 산술평균한 것의 역수. 즉, 조화평균을 H라 하면, 아래와 같은 공식이 된다. | n개의 양수 a1, a2,…,an에 대하여 그 역수 1/a1, 1/a2, …, 1/an을 산술평균한 것의 역수. 즉, 조화평균을 H라 하면, 아래와 같은 공식이 된다. | ||
| − | [[파일:조화평균 계산공식2.png|썸네일| | + | [[파일:조화평균 계산공식2.png|썸네일|400픽셀|가운데|조화평균 계산공식 2]] |
두 지점 A, B를 갈 때는 'a' km/h의 속도로, 올 때는 'b' km/h의 속도로 왕복했다면 이 사람의 평균속력은 a와 b의 조화평균에 해당된다. 또 100m를 3회 뛴 속력이 a,b,c일 때, 평균속력은 조화평균으로 구해진다. 이와 같이 일이나 능률의 예에서는 산술평균을 구하면 틀리게 된다. 산술평균 A, 기하평균 G, 조화평균 H 사이에는 H≤G≤A가 성립한다. 등호는 a1=a2=a3=…=an일 때이며, 또 그 때에 한하여 성립한다. 구간 a≤x≤b에서 적분가능인 함수 f(x)>0의 조화평균을 아래와 같은 공식으로 구하는 경우도 있다.<ref>〈[https://terms.naver.com/entry.naver?docId=1142224&cid=40942&categoryId=32206 조화평균]〉, 《두산백과》</ref> | 두 지점 A, B를 갈 때는 'a' km/h의 속도로, 올 때는 'b' km/h의 속도로 왕복했다면 이 사람의 평균속력은 a와 b의 조화평균에 해당된다. 또 100m를 3회 뛴 속력이 a,b,c일 때, 평균속력은 조화평균으로 구해진다. 이와 같이 일이나 능률의 예에서는 산술평균을 구하면 틀리게 된다. 산술평균 A, 기하평균 G, 조화평균 H 사이에는 H≤G≤A가 성립한다. 등호는 a1=a2=a3=…=an일 때이며, 또 그 때에 한하여 성립한다. 구간 a≤x≤b에서 적분가능인 함수 f(x)>0의 조화평균을 아래와 같은 공식으로 구하는 경우도 있다.<ref>〈[https://terms.naver.com/entry.naver?docId=1142224&cid=40942&categoryId=32206 조화평균]〉, 《두산백과》</ref> | ||
| − | [[파일:조화평균 계산공식3.png|썸네일| | + | [[파일:조화평균 계산공식3.png|썸네일|400픽셀|가운데|조화평균 계산공식 3]] |
== 조화평균의 정의 == | == 조화평균의 정의 == | ||
| 23번째 줄: | 23번째 줄: | ||
각자에게 주어진 같은 양의 식량을 갑은 일, 을은 일, 병은 일이면 모두 소비한다고 하자. 그러면 주어진 식량을 모두 모은 후 갑, 을, 병이 같이 소비한다면 식량이 모두 소비되기까지 걸릴 시간은 하루에 개인이 소비하는 식량의 양은 갑은 주어진 양의 1/20, 을은 1/25, 병은 1/40이다. 따라서 셋이서 하루에 소비하는 식량의 양은 개인에게 주어진 양의 1/20 + 1/25 + 1/40이다. 주어진 식량이 모두 소비되기까지 걸린 일수는 다음과 같이 20, 25, 40의 조화평균이다.<ref name="수학백과">〈[https://terms.naver.com/entry.naver?docId=3405320&cid=47324&categoryId=47324 조화평균]〉, 《수학백과》</ref> | 각자에게 주어진 같은 양의 식량을 갑은 일, 을은 일, 병은 일이면 모두 소비한다고 하자. 그러면 주어진 식량을 모두 모은 후 갑, 을, 병이 같이 소비한다면 식량이 모두 소비되기까지 걸릴 시간은 하루에 개인이 소비하는 식량의 양은 갑은 주어진 양의 1/20, 을은 1/25, 병은 1/40이다. 따라서 셋이서 하루에 소비하는 식량의 양은 개인에게 주어진 양의 1/20 + 1/25 + 1/40이다. 주어진 식량이 모두 소비되기까지 걸린 일수는 다음과 같이 20, 25, 40의 조화평균이다.<ref name="수학백과">〈[https://terms.naver.com/entry.naver?docId=3405320&cid=47324&categoryId=47324 조화평균]〉, 《수학백과》</ref> | ||
| − | [[파일:조화평균 계산 예1.png|썸네일| | + | [[파일:조화평균 계산 예1.png|썸네일|400픽셀|가운데|조화평균 계산 예1]] |
== 가중조화평균 == | == 가중조화평균 == | ||
| 32번째 줄: | 32번째 줄: | ||
서울에서 부산까지 가는데 처음 50km 구간은 시속 40km로, 다음 250km 구간은 시속 100km로, 마지막 100km 구간은 시속 80km로 달렸다면 평균속력은 아래와 같다. 이때 각 구간의 거리 이 50, 250, 100가중조화평균의 가중치 역할을 한다.<ref name="수학백과"></ref> | 서울에서 부산까지 가는데 처음 50km 구간은 시속 40km로, 다음 250km 구간은 시속 100km로, 마지막 100km 구간은 시속 80km로 달렸다면 평균속력은 아래와 같다. 이때 각 구간의 거리 이 50, 250, 100가중조화평균의 가중치 역할을 한다.<ref name="수학백과"></ref> | ||
| − | [[파일:조화평균 계산 예3.png|썸네일| | + | [[파일:조화평균 계산 예3.png|썸네일|400픽셀|가운데|조화평균 계산 예3]] |
== 다른 평균과의 관계 == | == 다른 평균과의 관계 == | ||
양의 실수 x1, x2, ..., xn에 대하여 산술평균, 조화평균, 기하평균을 각각 A(x1, x2, ..., xn), H(x1, x2, ..., xn), G(x1, x2, ..., xn)이라고 한다. | 양의 실수 x1, x2, ..., xn에 대하여 산술평균, 조화평균, 기하평균을 각각 A(x1, x2, ..., xn), H(x1, x2, ..., xn), G(x1, x2, ..., xn)이라고 한다. | ||
| − | [[파일:조화평균 계산 예4.png|썸네일| | + | [[파일:조화평균 계산 예4.png|썸네일|400픽셀|가운데|조화평균 계산 예4]] |
세 평균에 대하여 항상 다음 부등식이 성립한다. | 세 평균에 대하여 항상 다음 부등식이 성립한다. | ||
| − | [[파일:조화평균 계산 예5.png|썸네일| | + | [[파일:조화평균 계산 예5.png|썸네일|400픽셀|가운데|조화평균 계산 예5]] |
등식은 모든 xi들이 같을 때에만 성립한다.<ref name="수학백과"></ref> | 등식은 모든 xi들이 같을 때에만 성립한다.<ref name="수학백과"></ref> | ||
== 두 수의 조화평균 == | == 두 수의 조화평균 == | ||
| − | [[파일:두 수의 조화평균.png|썸네일| | + | [[파일:두 수의 조화평균.png|썸네일|400픽셀|가운데|두 수의 조화평균]] |
== 기하평균⸱산술평균⸱조화평균의 차이 == | == 기하평균⸱산술평균⸱조화평균의 차이 == | ||
2023년 2월 2일 (목) 16:51 판
조화평균(調和平均)은 주어진 수의 역수의 산술평균을 구한 것의 역수를 말한다.
목차
개요
조화평균은 주어진 집단의 측정결과에 대한 대표치의 하나로서 개별점수의 역(速)의 산술평균의 역(速)을 말한다. 각 개인별 측정치를 X1, X2, ...Xn이 라고 하고 전체 사례수를 N, 그리고 조화평균을 H라고 하면 다음과 같이 계산된다. 조화평균은 특별한 유형의 대표치로서 그 사용이 상당히 제한되어 있다. 그러나 어떤 특정한 자료를 요약하는 데 대표치로서 다른 대표치보다 우수하고 대표치로서 오차를 피할 수 있게 해준다. 예를 들면 시간비율의 평균 또는 특정한 물가계산에 적합하다. 또 통계에 있어서 평균의 표준오차는 사례수 N에 역비례하므로 평균의 표준오차의 통합에도 사용된다. 일반적으로 조화평균은 산술평균이 갖는 편견성(偏見性)에 역(速)으로 관계되고 있다. 경우에 따라서 조화 평균이 정확한 평균치를 돌려준다. 예를 들어, 전체 거리의 절반을 40km/h의 속도로 달리고, 남은 절반을 60km/h로 달렸다면, 평균 속력은 40과 60의 조화 평균인 48km/h가 된다. 이동하는데 전체 거리를 48 km/h의 속력으로 달린 경우와 같은 시간이 걸렸기 때문이다. (만약 전체 "시간"의 절반씩을 달렸다면, 평균 속력은 산술 평균인 50km/h가 된다.)[1][2]
n개의 양수에 대하여 그 역수들을 산술평균한 것의 역수를 조화평균이라 한다. 예를 들어, 두 지점 A, B를 갈 때는 'a' km/h의 속도로, 올 때는 'b' km/h의 속도로 왕복했다면 이 사람의 평균속력은 a와 b의 조화평균에 해당된다. 또 100m를 3회 뛴 속력이 a,b,c일 때, 평균속력은 조화평균으로 구해진다. 이와 같이 일이나 능률의 예에서는 산술평균을 구하면 틀리게 된다.
n개의 양수 a1, a2,…,an에 대하여 그 역수 1/a1, 1/a2, …, 1/an을 산술평균한 것의 역수. 즉, 조화평균을 H라 하면, 아래와 같은 공식이 된다.
두 지점 A, B를 갈 때는 'a' km/h의 속도로, 올 때는 'b' km/h의 속도로 왕복했다면 이 사람의 평균속력은 a와 b의 조화평균에 해당된다. 또 100m를 3회 뛴 속력이 a,b,c일 때, 평균속력은 조화평균으로 구해진다. 이와 같이 일이나 능률의 예에서는 산술평균을 구하면 틀리게 된다. 산술평균 A, 기하평균 G, 조화평균 H 사이에는 H≤G≤A가 성립한다. 등호는 a1=a2=a3=…=an일 때이며, 또 그 때에 한하여 성립한다. 구간 a≤x≤b에서 적분가능인 함수 f(x)>0의 조화평균을 아래와 같은 공식으로 구하는 경우도 있다.[3]
조화평균의 정의
양의 실수 x1, x2, ..., xn의 조화평균은 조화(harmonic)의 첫 글자 H를 이용하여 H(x1, x2, ..., xn)또는 간단히 H로 나타내며 다음과 같이 정의한다.
x1, x2, ..., xn의 조화평균은 역수 1/x1, 1/x2, ..., 1/xn의 산술평균의 역수이다.
각자에게 주어진 같은 양의 식량을 갑은 일, 을은 일, 병은 일이면 모두 소비한다고 하자. 그러면 주어진 식량을 모두 모은 후 갑, 을, 병이 같이 소비한다면 식량이 모두 소비되기까지 걸릴 시간은 하루에 개인이 소비하는 식량의 양은 갑은 주어진 양의 1/20, 을은 1/25, 병은 1/40이다. 따라서 셋이서 하루에 소비하는 식량의 양은 개인에게 주어진 양의 1/20 + 1/25 + 1/40이다. 주어진 식량이 모두 소비되기까지 걸린 일수는 다음과 같이 20, 25, 40의 조화평균이다.[4]
가중조화평균
양의 실수 x1, x2, ..., xn에 대하여 가중치 w1, w2, ..., wn이 주어진 경우 가중조화평균은 역수(1/x1, 1/x2, ..., 1/xn)의 가중산술평균의 역수로 정의한다. 모든 가중치가 같으면 가중조화평균은 조화평균과 일치한다.
서울에서 부산까지 가는데 처음 50km 구간은 시속 40km로, 다음 250km 구간은 시속 100km로, 마지막 100km 구간은 시속 80km로 달렸다면 평균속력은 아래와 같다. 이때 각 구간의 거리 이 50, 250, 100가중조화평균의 가중치 역할을 한다.[4]
다른 평균과의 관계
양의 실수 x1, x2, ..., xn에 대하여 산술평균, 조화평균, 기하평균을 각각 A(x1, x2, ..., xn), H(x1, x2, ..., xn), G(x1, x2, ..., xn)이라고 한다.
세 평균에 대하여 항상 다음 부등식이 성립한다.
등식은 모든 xi들이 같을 때에만 성립한다.[4]
두 수의 조화평균
기하평균⸱산술평균⸱조화평균의 차이
- 기하평균은 산술평균은 합의 평균이고, 기하평균은 곱의 평균이다. 예를 들어 첫번째 해에는 5%, 두 번째 해에는 10% 증가했다. 연평균 증가율 r로 2년 연속 증가한 값과, 5%, 10% 로 두 번 증가한 값이 같아야 한다. 이 예제를 일반화하면, 두 수 a, b의 기하평균이다. 곱의 평균을 기하 평균이라고 부르는 이유는, 기하의 비례식에서 유래하였기 때문인데, 예를 들어, 반원에서 직각 삼각형의 닮음식은 a : p = p : b이고, 여기서 p 가 a, b의 기하평균이다. 또다른 예로, 변의 길이가 a와 b인 직사각형과 넓이가 같은 정사각형의 한변의 길이는 a, b의 기하평균이다.
- 산술평균(算術平均, arithmetic mean)은 우리가 알고 있는 평균이다. 값을 모두 더하고, 기준이 되는 것의 개수로 나눈다. 예를 들어 두 수 a, b의 산술 평균은 이다.
- 조화평균(調和平均, harmonic mean)은 '역수의 산술평균의 역수'이다. 역수의 차원에서 평균을 구하고, 다시 역수를 취해 원래 차원의 값으로 돌아오는 것이다. 예를 들어 갈 때 10m/s, 올때 20m/s로 주행하였다. 10과 20의 산술평균인 15는 답이 아니다. 갈 때와 올 때 투여한 시간이 다르기 때문이다. 여기서는 시간의 차원에서 평균을 구해야 한다. 거리를 속력으로 나누면(역수), 시간인데, 이 시간의 평균을 구한 후에, 구한 시간 값에 대해, 다시 속력으로 바꾼 것이 평균 속력이다. 거리를 S라 하고, 시간에 대해 식을 세우면, S/10 + S/20 =2S/x이다. 이 예제를 일반화하여, 갈 때 속력을 a, 올 때 속력을 b라 하여 정리하면, 조화평균은 x = 2ab/a+b이다. 역수의 평균의 역수를 조화평균(harmonic mean)이라고 부르는 이유는, 음악의 화음(harmony)에서 이 평균을 찾을 수 있기 때문이다. 화음은 주파수가 1:2:3과 같이 간단한 정수 간격을 이룰 때 발생하는데, 현의 길이는 주파수의 역수이다. 즉 화음을 이루는 현의 길이를 구하기 위해서는, 역수(주파수)의 평균을 구하고, 다시 그 값의 역수(현의 길이)로 되돌아온다.[5]
동영상
각주
참고자료
- 〈조화 평균〉, 《위키백과》
- 〈조화평균〉, 《네이버 국어사전》
- 〈조화평균〉, 《교육학용어사전》
- 〈조화평균〉, 《두산백과》
- 〈조화평균〉, 《수학백과》
- 〈수학 용어를 알면 개념이 보인다 - 081. 산술평균 vs 기하평균 vs 조화평균〉, 《위키독스》
같이 보기

 위키원
위키원