"적도좌표계"의 두 판 사이의 차이
잔글 |
잔글 (→좌표계) |
||
| 7번째 줄: | 7번째 줄: | ||
== 좌표계 == | == 좌표계 == | ||
| − | [[좌표계]](座標系, coordinate reference system, CRS)는 [[좌표]]의 종류, 원점, 좌표축 따위를 통틀어 이르는 말이다. 또는 [[지구]] 표면에 여러 줄의 [[위도선]]과 [[자오선]]을 그어 특정한 점의 위치를 나타낼 수 있도록 한 가상의 [[격자선]]을 말한다. | + | [[좌표계]](座標系, coordinate reference system, CRS)는 [[좌표]]의 종류, 원점, 좌표축 따위를 통틀어 이르는 말이다. 또는 [[지구]] 표면에 여러 줄의 [[위도선]]과 [[자오선]]을 그어 특정한 점의 위치를 나타낼 수 있도록 한 가상의 [[격자선]]을 말한다. 자리표계라고도 한다. 스칼라 튜플을 이용해 n차원 공간의 각 지점을 표현하는 방법을 말한다. 여기서 스칼라는 보통 실수, 경우에 따라서는 복소수나 다른 일반적인 환(ring)의 원소를 말하기도 한다. 복잡한 우주에서 스칼라는 우주 전체에 대해 효과적인 좌표계를 산출하지 못하기도 한다. 좌표를 나타내는 방법 중 하나인 데카르트 좌표계는 프랑스의 철학자이자 수학자인 르네 데카르트가 발명했다. 그는 천장에 붙어 있는 파리의 위치를 나타내는 방법에 대해 고민하다가 데카르트 좌표계를 발명해 냈다고 한다. 한국 교육과정상, 여기서 열거된 좌표계 중 데카르트 좌표계를 제외한 나머지(극좌표계, 원통좌표계, 구면좌표계)는 대학 미적분학, 공업수학, 전자기학에서 배운다. 그리고 복소평면은 전기전자공학과에서 페이저를 이용하여 교류 전원 회로를 분석할 때 사용한다. 좌표축의 정의역이 양의 실수 전체의 집합일 경우 로그 스케일 적용이 가능하다.<ref>〈[https://ko.wikipedia.org/wiki/%EC%A2%8C%ED%91%9C%EA%B3%84 좌표계]〉, 《위키백과》</ref><ref>〈[https://namu.wiki/w/%EC%A2%8C%ED%91%9C%EA%B3%84 좌표계]〉, 《나무위키》</ref> |
== 적도좌표 == | == 적도좌표 == | ||
2024년 2월 20일 (화) 15:07 기준 최신판
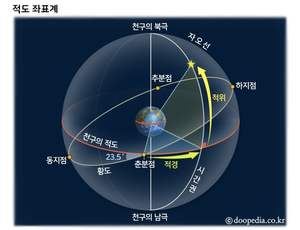
적도좌표계(赤道座標系, equatorial coordinate system)는 적경과 적위로 천체의 위치를 표시하는 좌표계를 말한다. 이러한 적도좌표계는 춘분점과 적도면을 기준으로 한다. 시간과 장소에 따라 변하는 지평좌표계와는 달리, 적도좌표계는 변하지 않는 고유한 값이므로, 천체를 관측하는 데는 유리하다.[1]
개요[편집]
적도좌표계는 천체의 위치를 나타내는 데 가장 일반적으로 사용되는 좌표계이다. 적도좌표계에서는 적경(right ascension)과 적위(declination)를 사용하여 천체의 위치를 나타낸다. 기본적으로 지구의 위경도 좌표계와 유사한 좌표계이다. 지구의 공전궤도면인 황도는 지구의 회전축이 기울어져 있기에 천구의 적도와 23° 26.5′의 황도경사각으로 기울어져 있다. 따라서 두 면은 천구 상에 분점(equinoxes)을 두 개 만든다. 이 중에서 태양이 황도를 따라서 동쪽으로 진행하다가 적도와 만나는 점(남에서 북으로 지나면서 끊는 점)이 춘분점이다. 보통 3월 21일 경에 태양이 춘분점(α = 0 h, δ = 0°, vernal equinox)을 지난다. 황도와 적도가 만나는 두 분점 중에서 태양이 황도를 따라 북에서 남으로 지나면서 적도를 끊는 점이 추분점이다. 9월 23일 경에 태양은 추분점(α=12 h, δ=0°, autumnal equinox)에 위치한다. 태양이 황도상에서 가장 북쪽에 위치하게 되는 점이 하지점(α=6 h, δ=23.5°, summer solstice)이며, 북반구에서는 일 년 중 가장 낮이 길며, 6월 22일 경이다. 태양이 적도 이남 남회귀선인 23.5°인 동지점(α=18 h, δ=-23.5°, winter solstice)에 도달하면 북반구에서는 밤이 가장 길다. 반면 남반구에서는 낮이 가장 길고, 밤이 가장 짧다. 이 시기는 12월 22일경이다.[2][3]
좌표계[편집]
좌표계(座標系, coordinate reference system, CRS)는 좌표의 종류, 원점, 좌표축 따위를 통틀어 이르는 말이다. 또는 지구 표면에 여러 줄의 위도선과 자오선을 그어 특정한 점의 위치를 나타낼 수 있도록 한 가상의 격자선을 말한다. 자리표계라고도 한다. 스칼라 튜플을 이용해 n차원 공간의 각 지점을 표현하는 방법을 말한다. 여기서 스칼라는 보통 실수, 경우에 따라서는 복소수나 다른 일반적인 환(ring)의 원소를 말하기도 한다. 복잡한 우주에서 스칼라는 우주 전체에 대해 효과적인 좌표계를 산출하지 못하기도 한다. 좌표를 나타내는 방법 중 하나인 데카르트 좌표계는 프랑스의 철학자이자 수학자인 르네 데카르트가 발명했다. 그는 천장에 붙어 있는 파리의 위치를 나타내는 방법에 대해 고민하다가 데카르트 좌표계를 발명해 냈다고 한다. 한국 교육과정상, 여기서 열거된 좌표계 중 데카르트 좌표계를 제외한 나머지(극좌표계, 원통좌표계, 구면좌표계)는 대학 미적분학, 공업수학, 전자기학에서 배운다. 그리고 복소평면은 전기전자공학과에서 페이저를 이용하여 교류 전원 회로를 분석할 때 사용한다. 좌표축의 정의역이 양의 실수 전체의 집합일 경우 로그 스케일 적용이 가능하다.[4][5]
적도좌표[편집]
천구상에서 천체의 위치를 나타내기 위해 쓰이는 구면좌표로 기준이 되는 면은 하늘의 적도이고, 춘분점을 원점으로 한다. 춘분점에서 천체까지 서쪽에서 동쪽으로(반시계방향) 측정한 각도를 적경이라 하며, 하늘의 적도면에서 천체까지의 각을 적위라 한다. 기준이 되는 면은 하늘의 적도로, 이것과 황도면과의 교점이 되는 춘분점을 원점으로 잡고, 서쪽에서 동쪽으로(반시계방향) 측정한 각도를 적경이라 하여 0°~360°의 각도 또는 0ʰ~24ʰ의 시간으로 나타낸다. 적도면에서 천체까지 시간권 내에서 잰 각은 적위라 하여 북쪽 방향을 양(+)으로, 남쪽 방향을 음(-)으로 하여 0°~±90°사이의 값으로 나타낸다. 항성에 대해서 적도좌표의 값은 시간과 함께 변하지 않으므로 성도나 항성 목록에 이용된다. 그러나 천구의 적도와 춘분점의 위치를 모르면 천체를 찾을 수 없다는 단점이 있다.[6]
일반적인 특징[편집]
관측자의 위치와 관측 시간에 따라 천체의 좌표값이 달라지는 지평좌표계(horizontal coordinate system)에서와 달리 적도좌표계에서는 천구에 투영된 천체의 좌표값은 모든 관측자에게 동일하다. 천구에 투영된 천체의 거리가 충분히 멀다는 조건이 성립하는 한 적도좌표계가 갖는 장점이다.
적경은 춘분점을 지나는 시간권을 기준으로 천체가 속한 시간권(hour circle)까지 반시계방향으로 측정한 각이다. 적경은 춘분점으로부터 동쪽으로 0~24시(h)로 표시하며 RA 혹은 로 나타낸다. 따라서, 1h는 15°에 해당한다. 적위는 지구의 위도와 비슷한 개념이고 로 나타낸다. 천구의 적도에서 시작하여 수직하게 시간권을 따라 측정하며 북극 방향은 양수이고 남극 방향은 음수이다. 즉, 천구의 적도에 위치한 천체는 δ=0°이다. 천구의 북극은 δ=90°에, 남극은 δ=-90°에 해당한다.
지구 자전축의 세차운동 때문에 기준점에 해당하는 춘분점의 위치가 시간에 따라 달라지므로 천구의 고정된 위치에 있는 천체의 적경과 적위는 엄밀한 의미로 말하면 해마다 달라진다. 이에 따라 적도좌표계를 사용하여 천구에 고정된 천체의 위치를 가리키기 위해서는 기준 연도 혹은 역기점(Epoch)을 정하고 이 때의 춘분점으로부터 적경과 적위를 나타내야 한다. 성도나 천체의 목록에 표시된 적경과 적위에 역기점 표시되어 있는 이유가 그것이다. 관측하는 시점에서의 정확한 적경과 적위를 알기 위해서는 기준 시점과 관측 시점의 차이만큼 보정해야 한다.[3]
세차운동[편집]
적도 부분이 부푼 지구는 지구의 자전축이 황도면과 백도면에 대하여 기울어져 있기 때문에 달과 태양으로부터 돌림힘(torque)을 받고 있다. 결과적으로 지구의 자전축이 연직 방향에 대하여 돌게 되는데 이 운동을 세차라고 부른다. 현재 북극성이 천구의 북극에 약 1° 떨어져 있지만 약 3200년이 지나면 세페이드자리의 감마성이 북극의 위치를 가리키게 된다(그림 2 참조). 약 8000년 후에는 백조 자리의 데네브가, 그리고 약 1만 2천년이 지나면 거문고 자리의 직녀성이 천구의 북극에 가깝게 자리하게 된다.
천구의 적도면과 황도면이 만나는 교선이 세차에 의하여 달라지므로 지구 자전축의 세차를 춘분점 세차(precession of the equinoxes)라고도 말한다. 세차운동에 의해 춘분점이 이동하는 속도는 1년에 50.25″이며, 춘분점이 천구의 적도를 따라 한바퀴 도는데 걸리는 시간은 약 2만5천800년이다. 지구 자전축의 세차운동 때문에 춘분점의 위치가 시간이 따라 달라지므로 적도좌표계를 사용하여 천구에 고정된 천체의 위치를 가리키기 위해서는 역기점을 정하고 이 때의 춘분점으로부터 적경과 적위를 나타내야 한다. 관측하는 시점에서의 정확한 적경과 적위는 역기점과 관측 시점의 차이만큼 보정해야 한다.
다양한 역기점이 사용되고 있지만 현재 표준이라고 할 수 있는 역기점은 1976년에 국제천문연맹(IAU)가 1984년부터 사용하자고 제안한 J2000.0이다. J2000.0의 'J'는 1년을 365.25일로 산정하는 율리우스력을 의미하며, '2000.0'은 2000년부터 시작되는 것임을 의미한다.
J2000.0은 다음과 같이 정의된다.
- 1. 율리우스력으로 2451545.0 지구 시간(TT, Terrestrial Time) 또는 2000년 1월 1일 정오(TT)
- 2. 국제원자시로 2000년 1월 1일 11시 59분 27.816초(TAI)
- 3. 협정 세계시로 2000년 1월 1일 11시 58분 55.816초(UTC)[3]
적도의식가대[편집]
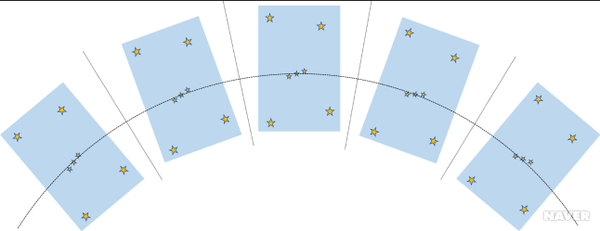
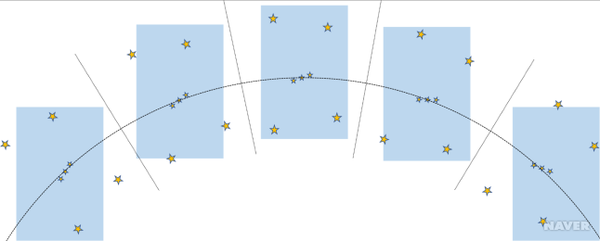
지구 자전축과 평행한 회전축을 가진 가대이다. 적도의식 가대의 장점은 일정한 속도로 극축을 중심으로 회전하면 일주운동을 하는 천체의 추적이 가능하다는 점이다. 지구 자전축과 나란하게 설정된 극축의 회전으로 시간각(혹은 적경)을 측정할 수 있고, 이와 수직을 이루고 있는 적위축의 회전을 따라 적위값을 측정할 수 있기 때문이다. 천구에 고정된 천체를 추적하기 위해 두 축 따라 움직여야하는 경위대식가대(altazimuth mount)와 달리 초점면에서 천체의 이미지가 회전하지 않는다는 또 다른 장점을 갖는다(그림 3, 4 참조). 이런 장점들이 있기 때문에 적도의식가대는 여러 방식으로 개발되어 개선되어 왔다. 주요 방식으로는 독일식적도의(German equatorial mount), 포크식적도의(open fork mount), 요크식적도의(yoke mount), 영국식적도의(English mount), 말발굽식적도의(horseshoe mount) 등이 있다(그림 5 참조).[3]
동영상[편집]
각주[편집]
참고자료[편집]
같이 보기[편집]

 위키원
위키원