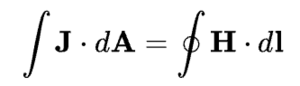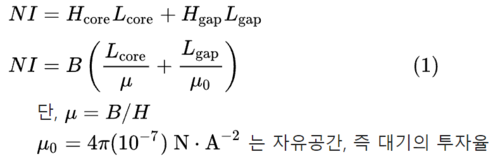"전자석"의 두 판 사이의 차이
잔글 (1.240.0.90(토론)의 편집을 Asadal의 마지막 판으로 되돌림) |
|||
| (사용자 3명의 중간 판 8개는 보이지 않습니다) | |||
| 26번째 줄: | 26번째 줄: | ||
아래의 표는 관련 이론의 수식에 표시된 기호들을 정의한 것이다. | 아래의 표는 관련 이론의 수식에 표시된 기호들을 정의한 것이다. | ||
| − | [[파일:이론 수식에 표시된 기호.png|썸네일|500픽셀|가운데|]] | + | [[파일:이론 수식에 표시된 기호.png|썸네일|500픽셀|가운데|]] |
전자석이 만들어내는 자기장은 [[앙페르 회로 법칙]]으로 설명할 수 있다. | 전자석이 만들어내는 자기장은 [[앙페르 회로 법칙]]으로 설명할 수 있다. | ||
| − | [[파일:앙페르 회로 법칙.png|썸네일|300픽셀|가운데|]] | + | [[파일:앙페르 회로 법칙.png|썸네일|300픽셀|가운데|]] |
즉, 전류가 흐르는 전기 회로에서 전선 주위에 형성되는 자기장의 세기는 전류의 세기에 비례한다. 이는 비오-사바르 법칙으로도 설명할 수 있다. 자기 코어에 의해 발생하는 자기력선의 세기와 자기장의 크기는 계산하기 어려운데, 이는 다음과 같은 까닭 때문이다. 우선은 자기력선이 자기 코어를 지나는 전자석의 두 극에서만 출발하는 것이 아니라 코일과 자기 코어의 사이에서도 형성된다는 점을 들 수 있다. 이를 누설 인덕턴스라고 하는데 전자석에서 필연적으로 발생하는 현상이다. 두 번째로는 자기 코어를 사용한 전자석에서 발생되는 자기장과 그에 의한 힘이 전류에 대해 비선형이라는 점을 들 수 있다. 이러한 이유로 전자석에 의해 발생되는 자기장의 계산에는 유한요소법이 쓰인다. | 즉, 전류가 흐르는 전기 회로에서 전선 주위에 형성되는 자기장의 세기는 전류의 세기에 비례한다. 이는 비오-사바르 법칙으로도 설명할 수 있다. 자기 코어에 의해 발생하는 자기력선의 세기와 자기장의 크기는 계산하기 어려운데, 이는 다음과 같은 까닭 때문이다. 우선은 자기력선이 자기 코어를 지나는 전자석의 두 극에서만 출발하는 것이 아니라 코일과 자기 코어의 사이에서도 형성된다는 점을 들 수 있다. 이를 누설 인덕턴스라고 하는데 전자석에서 필연적으로 발생하는 현상이다. 두 번째로는 자기 코어를 사용한 전자석에서 발생되는 자기장과 그에 의한 힘이 전류에 대해 비선형이라는 점을 들 수 있다. 이러한 이유로 전자석에 의해 발생되는 자기장의 계산에는 유한요소법이 쓰인다. | ||
| 37번째 줄: | 37번째 줄: | ||
전류에 의해 형성된 자기장은 전선을 감은 횟수인 '''N'''과 전류이 세기인 '''I'''에 비례한다. 암페어-횟수를 뜻하는 '''NI'''는 기자력을 나타낸다. 단일 자기 회로로 된 전자석에서 앙페르의 회로 법칙을 적용할 때에는 자기 코어의 길이인 '''Lcore '''과 자기 코어와 코일 사이의 간극의 길이인 '''Lgap'''' 을 모두 고려하여야 한다. | 전류에 의해 형성된 자기장은 전선을 감은 횟수인 '''N'''과 전류이 세기인 '''I'''에 비례한다. 암페어-횟수를 뜻하는 '''NI'''는 기자력을 나타낸다. 단일 자기 회로로 된 전자석에서 앙페르의 회로 법칙을 적용할 때에는 자기 코어의 길이인 '''Lcore '''과 자기 코어와 코일 사이의 간극의 길이인 '''Lgap'''' 을 모두 고려하여야 한다. | ||
| − | [[파일:비선형 방정식.png|썸네일|500픽셀|가운데|]] | + | [[파일:비선형 방정식.png|썸네일|500픽셀|가운데|]] |
| − | |||
위의 식은 비선형 방정식인데 자기 코어의 투자율 '''μ'''이 자기장 '''B'''에 의해 변화하기 때문이다. 정확하게는 자기 코어의 투자율 '''μ'''은 자기장 '''B'''에 대해 이력 곡선을 나타낸다. 자기장의 크기를 알 수 없을 경우 방정식의 해는 수치 해석을 사용하여 근삿값을 구한다. 한편, 기자력이 자기 포화에 이르면 자기 코어 역시 포화되기 때문에, 포화 상태에 이른 자기 코어의 자력은 '''NI'''에 비례하게 된다. 자기 코어와 코일 사이의 간극이 무시할 수 있을 정도로 작은 경우 매 미터당 800 암페어-횟수 이상이면 이력 현상은 고려하지 않아도 좋을 정도로 미미하다. | 위의 식은 비선형 방정식인데 자기 코어의 투자율 '''μ'''이 자기장 '''B'''에 의해 변화하기 때문이다. 정확하게는 자기 코어의 투자율 '''μ'''은 자기장 '''B'''에 대해 이력 곡선을 나타낸다. 자기장의 크기를 알 수 없을 경우 방정식의 해는 수치 해석을 사용하여 근삿값을 구한다. 한편, 기자력이 자기 포화에 이르면 자기 코어 역시 포화되기 때문에, 포화 상태에 이른 자기 코어의 자력은 '''NI'''에 비례하게 된다. 자기 코어와 코일 사이의 간극이 무시할 수 있을 정도로 작은 경우 매 미터당 800 암페어-횟수 이상이면 이력 현상은 고려하지 않아도 좋을 정도로 미미하다. | ||
| 57번째 줄: | 56번째 줄: | ||
코일 가운데 철심을 넣는 대신 자성체로 된 탄자를 넣어 쏘아내면 코일건이 된다. 이걸 고리 모양으로 만든 것이 토로이드로 핵융합 장치 중 하나인 토카막을 만들 때 사용된다. | 코일 가운데 철심을 넣는 대신 자성체로 된 탄자를 넣어 쏘아내면 코일건이 된다. 이걸 고리 모양으로 만든 것이 토로이드로 핵융합 장치 중 하나인 토카막을 만들 때 사용된다. | ||
| − | === 초전도 전자석 == | + | === 초전도 전자석 === |
초전도 전자석은 초전도 현상을 이용한 전자석으로, 초전도 상태에서 내부 저항은 0이고 [[옴의 법칙]]에 따라 전류는 무한에 가까운 것을 이용, 당연히 전류가 폭발적으로 치솟으니 자기장도 그만큼 세게 형성되는 것을 이용한 것이다. 또 자기 포화 상태를 방지할 수도 있다. 다만 초전도 현상이 일어나야 저러한 장점을 사용할 수 있으므로, 초전도 상태를 유지해야 하며, 이 때문에 매우 낮은 온도에서 작동될 수 밖에 없다. 이때 냉각제로서 액체 헬륨을 주로 사용한다. | 초전도 전자석은 초전도 현상을 이용한 전자석으로, 초전도 상태에서 내부 저항은 0이고 [[옴의 법칙]]에 따라 전류는 무한에 가까운 것을 이용, 당연히 전류가 폭발적으로 치솟으니 자기장도 그만큼 세게 형성되는 것을 이용한 것이다. 또 자기 포화 상태를 방지할 수도 있다. 다만 초전도 현상이 일어나야 저러한 장점을 사용할 수 있으므로, 초전도 상태를 유지해야 하며, 이 때문에 매우 낮은 온도에서 작동될 수 밖에 없다. 이때 냉각제로서 액체 헬륨을 주로 사용한다. | ||
| − | NMR, | + | [[NMR]], [[MRI]] 등의 [[자기장]]을 이용한 측정장비에 자주 사용되며, LHC도 [[초전도자석]]을 이용하여 [[입자]]를 가두어 놓는다. |
== 실생활에서의 전자석 == | == 실생활에서의 전자석 == | ||
| − | * | + | * [[폐차장]]에서 차를 옮길 때 전자석을 사용해 옮긴다. 들어올릴 땐 [[전기]]를 내보내 [[자성]]을 띠게 만들어 차를 들어올리고, 차를 내릴 땐 전기를 꺼서 자성을 없애는 방식이다. |
* 전기차단기는 일정 수준 이상의 과도한 전류가 흐르면 전자석이 작동해 스위치를 내리는 방식이다. | * 전기차단기는 일정 수준 이상의 과도한 전류가 흐르면 전자석이 작동해 스위치를 내리는 방식이다. | ||
* 전기를 동력으로 바꾸는 전동기는 유형을 막론하고 전부 영구자석과 전자석을 조합하여 자석끼리 밀고 당기는 성질을 이용하여 동력을 일으킨다. | * 전기를 동력으로 바꾸는 전동기는 유형을 막론하고 전부 영구자석과 전자석을 조합하여 자석끼리 밀고 당기는 성질을 이용하여 동력을 일으킨다. | ||
| 75번째 줄: | 74번째 줄: | ||
== 같이 보기 == | == 같이 보기 == | ||
| + | * [[전기]] | ||
| + | * [[자석]] | ||
* [[전자기학]] | * [[전자기학]] | ||
| − | * [[ | + | * [[초전도자석]] |
* [[영구자석]] | * [[영구자석]] | ||
| − | {{ | + | {{전기|검토 필요}} |
| + | {{도구}} | ||
2024년 9월 6일 (금) 09:47 기준 최신판
전자석(電磁石, electromagnet)은 전류가 흐르는 동안 자기장이 형성되는 자석이다. 전류가 흐르지 않으면 자기장이 사라진다.
전류의 공급과 상관없이 항상 자기(磁氣)를 유지하는 영구자석과 구분된다. 도선에 전류가 흐르면 도선 주위에 동심원 모양의 자기장이 형성된다. 이러한 원리를 이용하여 영구자석으로는 얻을 수 없는 매우 강력한 자기장을 얻을 수 있다. 전자석의 철심은 어느 정도 자기화가 진행되면 전류를 더 높여도 더 이상 자기화가 진행되지 않는다. 이를 자기포화(磁氣飽和)상태라고 한다.
전자석은 전류를 인위적으로 조정하여 비교적 쉽게 자기장의 세기를 바꿀 수 있다. 그래서 통신기의 계전기부터 1t(톤) 이상의 무거운 재료를 끌어올리는 전자기식 기중기까지 널리 이용된다.
개요[편집]
앙페르 회로 법칙에서 나타내는 바와 같이 직류가 흐르는 전선은 주변에 자기장이 형성된다. 이때 형성되는 자기장의 세기는 전류의 세기에 비례한다.
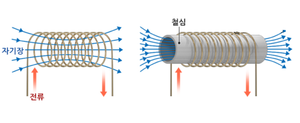
코일 형태로 감긴 전선에 전류가 흐르면 자기장이 중첩되어 일정한 극성을 띄게 된다. 이는 코일의 주변에 생성된 자기력선이 중첩되면서 코일의 중앙에 한 방향으로 작용하는 자기력선이 발생하기 때문이다. 코르크스크류와 같은 모양의 나선을 그리는 코일을 원통 모양으로 만든 것을 솔레노이드라고 하고, 양 끝을 한 곳으로 모아 둥글게 만든 것은 환형 인덕터라고 한다. 형성된 자기장을 보다 강하게 하기 위해 코일의 중앙에 철과 같은 강자성을 띄는 물질로 만든 자기 코어를 놓는 것이 일반적이다. 이는 투자율이 높은 자기 코어를 쓰면 자력선이 보다 강력해지기 때문이다.[1][2] 엄지를 세우고 오른손을 말아 쥐었을 때 검지 내지 단지가 말린 방향을 전류의 흐름이라고 하면 엄지가 가리키는 방향이 자기력선의 방향, 즉 N극이 된다.
전자석은 영구자석과 달리 전류가 흐를 때만 자성을 띄므로 자성을 조절하여야 하는 여러 곳에 두루 쓰인다.
자기 코어의 역할[편집]
철과 같은 강자성 물질로 만든 자기 코어는 자구라고 하는 작은 구획들로 되어있다. 전류가 흐르기 전에 자구들은 특정한 방향이 없이 무작위적으로 배열되어 있기 때문에 결과적으로 자성을 띄지 않는 상태가 된다. 하지만 코일에 전류가 흐르고 자기력선이 형성되면 자기 코어의 자구들은 자기력선을 따라 배열되고 영구자석과 같은 자력선을 나타내게 된다. 이 때문에 코일이 만드는 자기력선과 자기 코어의 자기력선이 더해져 보다 강력한 자기장을 만들게 된다. 특정 전류가 만들어 낼 수 있는 자기장이 정해져 있으므로 자기 코어에 의해 형성되는 자기장 역시 일정 정도 이상 세기가 증가하지는 않는다. 전자석이 만들어 낼 수 있는 최대 크기의 자력에 도달하는 것을 자기 포화라고 한다.
코일에 전류가 흐르지 않게 되면 자기 코어의 자구들은 다시 원래의 방향으로 무작위적인 극성을 나타내게 되고, 그 결과 자기장을 잃는 이력 현상이 나타나 자성을 잃게 된다. 이 때 일부 자구는 전류가 흐르던 때에 배열되었던 자기 방향을 유지하는데 이를 잔류 자기라고 한다. 잔류 자기가 클 경우 자기 코어는 전류가 끊긴 상태에서도 약한 자성을 일정 기간 띌 수 있다. 전자석을 이용할 때 잔류 자기는 기계의 동작에 방해가 되므로 자기 코어의 자성을 소거하여야 한다.
역사[편집]
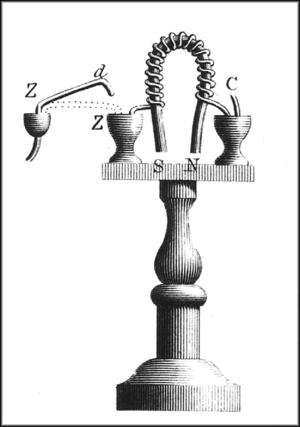
덴마크의 과학자 한스 크리스티안 외르스테드는 1820년 전류가 자기장을 만든다는 것을 발견하였다. 영국의 과학자 윌리엄 스터전은 1824년 전류에서 발생하는 자기장을 이용하여 전자석을 만들었다. 스터전이 처음 만든 전자석은 말굽 모양의 철심을 자기 코어로 이용한 것이었다. 스터전은 자기 코어에 굵은 구리 전선을 18 번 감아 전자석을 만들었다. 당시에는 오늘날과 같은 절연체가 없었기 때문에 스터전은 구리 도선에 바니시를 발라 절연체로 사용하였다. 스터전의 전자석은 약 200g을 들어올릴 수 있었으며 전지들을 연결하여 전류를 높이자 약 4kg의 물체도 들어올렸다. 1827년이 되자 미국의 과학자 조지프 헨리가 대중적으로 널리 알려지게 된 전자석을 선보였다. 헨리가 만든 전자석은 비단을 여러겹 감아 절연한 구리선을 자기 코어에 수천 번 감아 만든 것으로 강한 전류를 사용하여 2063 파운드를 들어 올렸다. 전자석을 처음으로 응용한 기계는 전신음 발생기였다.
1906년 프랑스 과학자 피에르 바이스는 강자성을 띄는 자기 코어에 의해 전자석의 자기장이 강해지는 것을 설명하기 위해 자구 이론을 도입하였다. 1920년대에 이르러 베르너 하이젠베르크, 레프 란다우, 펠릭스 블로흐 등의 과학자들은 강자성을 양자역학으로 설명하는 이론을 제시하였다.
관련 이론[편집]
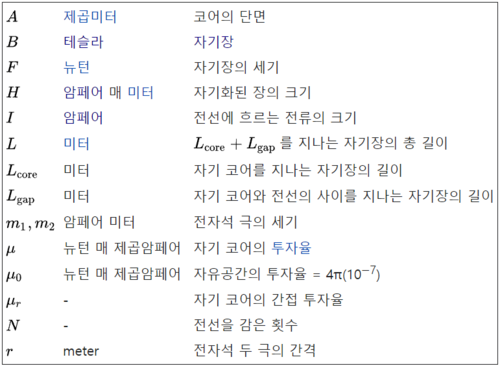
아래의 표는 관련 이론의 수식에 표시된 기호들을 정의한 것이다.
전자석이 만들어내는 자기장은 앙페르 회로 법칙으로 설명할 수 있다.
즉, 전류가 흐르는 전기 회로에서 전선 주위에 형성되는 자기장의 세기는 전류의 세기에 비례한다. 이는 비오-사바르 법칙으로도 설명할 수 있다. 자기 코어에 의해 발생하는 자기력선의 세기와 자기장의 크기는 계산하기 어려운데, 이는 다음과 같은 까닭 때문이다. 우선은 자기력선이 자기 코어를 지나는 전자석의 두 극에서만 출발하는 것이 아니라 코일과 자기 코어의 사이에서도 형성된다는 점을 들 수 있다. 이를 누설 인덕턴스라고 하는데 전자석에서 필연적으로 발생하는 현상이다. 두 번째로는 자기 코어를 사용한 전자석에서 발생되는 자기장과 그에 의한 힘이 전류에 대해 비선형이라는 점을 들 수 있다. 이러한 이유로 전자석에 의해 발생되는 자기장의 계산에는 유한요소법이 쓰인다.
전류와 자기장[편집]
전류에 의해 형성된 자기장은 전선을 감은 횟수인 N과 전류이 세기인 I에 비례한다. 암페어-횟수를 뜻하는 NI는 기자력을 나타낸다. 단일 자기 회로로 된 전자석에서 앙페르의 회로 법칙을 적용할 때에는 자기 코어의 길이인 Lcore 과 자기 코어와 코일 사이의 간극의 길이인 Lgap' 을 모두 고려하여야 한다.
위의 식은 비선형 방정식인데 자기 코어의 투자율 μ이 자기장 B에 의해 변화하기 때문이다. 정확하게는 자기 코어의 투자율 μ은 자기장 B에 대해 이력 곡선을 나타낸다. 자기장의 크기를 알 수 없을 경우 방정식의 해는 수치 해석을 사용하여 근삿값을 구한다. 한편, 기자력이 자기 포화에 이르면 자기 코어 역시 포화되기 때문에, 포화 상태에 이른 자기 코어의 자력은 NI에 비례하게 된다. 자기 코어와 코일 사이의 간극이 무시할 수 있을 정도로 작은 경우 매 미터당 800 암페어-횟수 이상이면 이력 현상은 고려하지 않아도 좋을 정도로 미미하다.
대부분의 자기 코어는 μr = μ/μ₀ ≈ 2000-6000 정도의 투자율을 보이는 강자성 물질을 사용한다. 따라서 위의 식 (1)에서 두 번째 식은 일반적으로 고려되지 않는데, 상용되는 전자석에서는 자기 코어의 투자율이 크고 코어와 코일 사이의 간극이 무시될 수 있을 정도로 작기 때문이다.
종류[편집]
솔레노이드[편집]
가장 간단한 형태. 여러분이 생각하는 바로 그 전자석이다. 원형의 철심을 코일로 둘러서 만든다. 초등학교에서도 만드며, 효율이 좋지 않다. 철심이나 클립 몇 개 드는 정도다. 그마저도 못 들어 몇 개는 떨어지는 경우도 있긴 하다.
앞에서 언급된 맥스웰 방정식을 풀면 B=μ₀nI가 되고 따라서 n을 충분히 늘리면 강력한 자기장을 얻을 수 있는 이점이 있어 자주 사용된다.
스프링과 솔레노이드를 결합하면 전자 피스톤을 만들 수도 있다. 평소에 스프링의 힘으로 한쪽으로 누르고 있다가, 전기를 흘려보내면 전자기력에 의해 스프링이 누르던 방향 반대편으로 움직이는 얼개로 된 것이 가장 흔한 방식이다. 전기 모터와 감속기어 등을 붙여 피스톤처럼 움직이는 전기식 구동장치에 비하면 힘은 약하지만, 구조가 간단하고 크기가 작으므로 일상용품이나 자동차 내부의 작은 기계장치 등 큰 힘이 필요치 않은 곳에 널리 쓰인다. 보통 이를 솔레노이드 작동기, 혹은 그냥 솔레노이드라 부른다.
이 솔레노이드 작동기를 응용하여 유체의 흐름 방향을 제어하는 밸브를 만들기도 하는데, 이를 특별히 솔레노이드 밸브라 부른다.
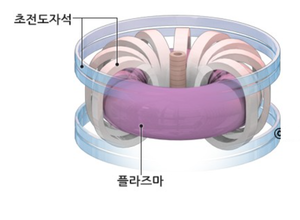
코일 가운데 철심을 넣는 대신 자성체로 된 탄자를 넣어 쏘아내면 코일건이 된다. 이걸 고리 모양으로 만든 것이 토로이드로 핵융합 장치 중 하나인 토카막을 만들 때 사용된다.
초전도 전자석[편집]
초전도 전자석은 초전도 현상을 이용한 전자석으로, 초전도 상태에서 내부 저항은 0이고 옴의 법칙에 따라 전류는 무한에 가까운 것을 이용, 당연히 전류가 폭발적으로 치솟으니 자기장도 그만큼 세게 형성되는 것을 이용한 것이다. 또 자기 포화 상태를 방지할 수도 있다. 다만 초전도 현상이 일어나야 저러한 장점을 사용할 수 있으므로, 초전도 상태를 유지해야 하며, 이 때문에 매우 낮은 온도에서 작동될 수 밖에 없다. 이때 냉각제로서 액체 헬륨을 주로 사용한다.
NMR, MRI 등의 자기장을 이용한 측정장비에 자주 사용되며, LHC도 초전도자석을 이용하여 입자를 가두어 놓는다.
실생활에서의 전자석[편집]
- 폐차장에서 차를 옮길 때 전자석을 사용해 옮긴다. 들어올릴 땐 전기를 내보내 자성을 띠게 만들어 차를 들어올리고, 차를 내릴 땐 전기를 꺼서 자성을 없애는 방식이다.
- 전기차단기는 일정 수준 이상의 과도한 전류가 흐르면 전자석이 작동해 스위치를 내리는 방식이다.
- 전기를 동력으로 바꾸는 전동기는 유형을 막론하고 전부 영구자석과 전자석을 조합하여 자석끼리 밀고 당기는 성질을 이용하여 동력을 일으킨다.
- 자기부상열차도 전자석으로 움직인다.
- 반도체를 이용한 SRAM이 개발되기 전인 1950~60년대에는 작은 전자석에 1비트씩을 저장하는 자기 코어 메모리(Magnetic Core Memory)가 주력으로 사용되었다. 코어 메모리는 아폴로 11호의 항법 컴퓨터에도 사용되었고, 용량은 72KB였다.
참고자료[편집]
같이 보기[편집]
| ||||||||||||||||||||||||||

 위키원
위키원