기하광학

기하광학(幾何光學, Geometrical optics, Ray optics)은 빛의 파동성과 양자성 등을 무시하고 빛의 진행선 특성만을 기하학적으로 연구하는 광학 분야이다. 광학기기의 설계에 중요한 위치를 차지한다. 현미경이나 망원경과 같은 광학기기를 만드는 데 주로 응용된다.

회절이나 간섭 등 빛의 파동적인 면을 연구하는 파동광학에 대응하는 광학의 한 부문으로, 균일한 매질 속에서는 직진하고, 다른 매질과의 경계면에서는 반사 및 굴절하는 성질을 가진 물질로서의 빛을 다룬다. 빛의 통로가 그 파장만큼 좁을 때나 광학계(光學系)를 이용한 상의 미세한 부분을 살필 때 등을 제외하면, 근사적이기는 하나 매우 유효하게 빛의 경로나 상이 맺히는 모양을 연구할 수 있다. 현미경 ·망원경 등 광학기계의 설계에 중요한 학문이다.

개요

기하광학은 빛의 진행을 아주 작은 입자의 운동으로 보아 그 궤적을 광선으로 나타내고, 광선의 진행을 지배하는 세 가지 기본 법칙(직진, 반사, 굴절 법칙)을 써서 광학 현상을 이해하는 학문 분야이다. 광선의 경로는 직선 또는 곡선으로 나타내며, 그것을 기술하거나 분석할 때는 기하학의 기본 개념과 법칙을 쓰게 되므로 기하광학이라고 한다.

기하광학의 기본 법칙과 개념은 안경, 사진기, 현미경, 망원경 등 각종 결상기기, 분광계나 편광계 등의 계측기기, 전등이나 자동차 전조등과 같은 조명기기 등 갖가지 광학기기의 설계 및 성능 분석을 할 때 이론적 도구로 쓰인다.

기하광학의 법칙

광선의 진행에 관한 다음 세 가지 기본 법칙을 말하며, 페르마(P. Fermat, 1601-1665)의 최소 시간의 원리에서 끌어낼 수 있다

입사면과 입사각, 반사각, 굴절각의 정의

1) 직진 법칙, 2) 반사 법칙, 3) 굴절 법칙.

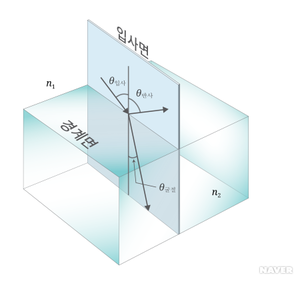
직진 법칙은 빛이 균일한 매질 속의 한 곳에서 다른 곳으로 갈 때 광선은 두 점을 잇는 직선을 따라 간다는 것이다. 광선이 진행하다가 굴절률이 다른 두 매질의 평면 경계면을 만나면, 그림 1과 같이, 일부는 그 경계면에서 반사되고, 일부는 경계면에서 꺾여 다른 매질로 들어간다. 반사 법칙은 반사광선의 반사각 θ반사가 입사광선의 입사각 θ입사와 같다는 것이다.

θ반사=θ입사

굴절 법칙은 굴절광선의 굴절각 θ굴절은 입사각과 다음 관계가 있다는 것이다.

n₁sinθ입사 = n₂sinθ굴절

여기에서 n₁과 n₂는 각각 첫째 및 둘째 매질의 굴절률이다.

매질이 굴절률이 균일하지 않아 위치의 함수 n(r)이 될 때는 광선의 진행 방향은 다음 아이코날(eikonal) 방정식에 따라 결정된다.

|∇s(r)| = n(r)

여기에서 s(r)은 광선 위의 한 점을 기준으로 잡아 광선을 따라 잰 거리이다.

기하광학의 특징

• 광선추적 및 렌즈방정식과 같은 작도법을 이용하여 주로 설명, 해석을 함
• 빛과 렌즈,거울,프리즘,개구(빛의 파장 보다 훨씬 큰 물체들)와의 상호작용에 관심을 갖음

기하광학의 구분

• 근축 광학 (Paraxial) : 한 점에서 나온 광선이 완전히 한 점에 모이는 현상을 다룸 (수차가 없음)

• 근축 광선 (paraxial rays) : 광축에 대해 작은 각도로 입사하는 광선

• 수차론 (Aberration) : 점 광원에서 출발한 광선들이 단일한 점으로 모이지 않고 흩어지는 현상을 다룸

쓰임새

가장 중요한 쓰임새는 결상 이론으로서 기본 광학 소자인 렌즈와 거울의 광학적 특성 및 결상 조건, 그리고 상의 불완전성의 정도를 기술하는 수차 특성 등을 설명하고 또 정량적으로 분석하는데 쓰인다. 또한 프리즘이나 에돌이발을 쓰는 분광 계측 기기를 설계하고 성능을 예측할 때도 쓰인다. 따라서 모든 광학 현상을 분석하고 이해하는 데는 일차적으로 기하광학의 개념과 법칙을 쓴다.

기하광학의 사용 이유

• 사실, 빛은 파동성 성질로 볼 때 전자기파의 일종으로써,

• 전자기파의 전파(傳播)를 설명하는 맥스웰방정식으로,
• 광섬유를 통한 광의 도파(導播) 등을 거의 완벽하게 설명할 수 있으나,
• 광섬유내 광 코어의 직경이 광의 파장에 비해 큰 경우에는,
• 맥스웰방정식을 푼다는 것이 수학적으로 대단히 복잡해 짐

• 따라서, 파장을 0 으로 간주하여 설명하는 기하광학을 이용하여,

• 광섬유를 통한 광의 도파, 현미경이나 망원경 등 광학기계의 설계 등에 활용됨

• 한편, 빛의 간섭 및 회절 현상은 기하광학으로는 설명이 되지 않음

한계

기하광학은 많은 광학 현상을 놀라울 정도로 잘 기술하지만, 빛의 파동성 때문에 생기는 현상인 간섭, 회절, 편광을 기술하는데 필요한 개념을 반영하기 어렵다. 따라서 이 단점은 빛의 파동성을 반영하여 그 진행을 기술하는 물리광학(또는 파동광학)에서 보완한다. 또한 빛과 물질의 상호작용으로 빛이 생겨나거나 흡수될 때 그 에너지 변화가 hf(h는 플랑크상수 6.63×10‾³⁴ J·s; f는 빛의 진동수로 단위는 Hz)의 정수배 단위로 이루어진다는 양자성도 넣을 수 없다. 이 단점은 빛의 양자성을 반영하여 물질과의 상호작용을 기술하는 양자 광학에서 보완한다.

참고자료

• 〈기하광학〉, 《두산백과》
• 〈기하광학〉, 《물리학백과》
• 〈기하광학〉, 《위키백과》
• 〈Geometrical Optics, Ray Theory, Ray Optics 기하 광학, 광선 이론, 광선 광학, 선속 광학〉, 《정보통신기술용어해설》, 2021-07-11

같이 보기

• 광학
• 물리광학
• 양자광학
• 광학기기

이 기하광학 문서는 기술에 관한 글로서 검토가 필요합니다. 위키 문서는 누구든지 자유롭게 편집할 수 있습니다. [편집]을 눌러 문서 내용을 검토·수정해 주세요.

산업 : 산업, 산업혁명, 기술 □■⊕, 제조, 기계, 전자제품, 정보통신, 반도체, 화학, 바이오, 건설, 유통, 서비스, 에너지, 전기, 소재, 원소, 환경, 직업, 화폐, 금융, 금융사, 부동산, 부동산 거래, 부동산 정책, 아파트, 건물, 토지 기술 R&D • 개발 • 개선 • 개혁 • 건설기술 • 건축기술 • 계측 • 고급기술 • 고신기술 • 과학 • 과학기술 • 과학자 • 관찰 • 관측 • 군사기술 • 기능 • 기술 • 기술개발 • 기술개혁 • 기술격차 • 기술경쟁 • 기술력 • 기술발전 • 기술유출 • 기술자 • 기술진보 • 기술표준 • 기술혁명 • 기술혁신 • 기예 • 기초기술 • 나노기술 • 녹색기술 • 대체기술 • 문화기술 • 바이오기술 • 발전 • 방법 • 방법론 • 복합기술 • 상용화 • 생명공학기술 • 소멸 • 신기술 • 아이디어 • 엔지니어 • 엔지니어링 • 연구 • 연구개발 • 연구기관 • 연구소 • 연구원 (사람) • 연구원 (기관) • 연구자 • 우주항공기술 • 원리 • 원천기술 • 융합기술 • 응용기술 • 적정기술 • 전기기술 • 전문가 • 전문직 • 전자기술 • 정보 • 정보기술 • 정체 • 제어 • 지성 • 지식 • 지혜 • 진보 • 집단지성 • 첨단기술 • 최첨단기술 • 출연연 • 측정 • 토목기술 • 통신기술 • 퇴보 • 표준 • 표준화 • 하이테크 • 학문 • 학술 • 학자 • 핵심기술 • 혁명 • 혁신 • 혁신기술 • 현상 • 화학기술 • 환경기술 공학 건설공학 • 건축공학 • 계측공학 • 고분자공학 • 공간정보공학 • 공학 • 공학자 • 광공학 • 광학 • 교통공학 • 구조공학 • 금속공학 • 금속재료공학 • 금융공학 • 기계공학 • 기전공학 • 기하광학 • 기후공학 • 나노공학 • 도시공학 • 디스플레이공학 • 레이저공학 • 로봇공학 • 메카트로닉스 • 반도체공학 • 방산공학 • 배터리공학 • 산업공학 • 생명공학 • 생태공학 • 석유공학 • 섬유공학 • 세라믹공학 • 소방공학 • 소프트웨어공학 • 시스템공학 • 식품공학 • 신소재공학 • 신재생에너지공학 • 안전공학 • 에너지공학 • 에듀테크(교육공학) • 예술공학 • 원자력공학 • 유전공학 • 음향공학 • 의공학 • 인간공학 • 자동차공학 • 자원공학 • 재료공학 • 전기공학 • 전기기계공학 • 전기전자공학 • 전자공학 • 전파공학 • 정보경영공학 • 정보공학 • 정보통신공학 • 제약공학 • 제어계측공학 • 제어공학 • 조선공학 • 지진공학 • 지질공학 • 철도공학 • 컴퓨터공학(전산공학) • 토목공학 • 항공우주공학 • 해양공학 • 화장품공학 • 화학공학 • 환경공학 지식재산권 2차적 저작물 • 2차적 저작물 작성권 • 가수 • 가품 • 각본 • 각색 • 간행 • 간행물 • 건축저작물 • 게임 • 게재 • 결합저작물 • 공개 • 공공누리 저작권 • 공동저작물 • 공동저작자 • 공업소유권 • 공연 • 공연권 • 공유 • 공정이용 • 공중송신권 • 공표 • 공표권 • 그림 • 기계번역 • 기술인증 • 노래 • 녹음 • 녹취 • 녹취록 • 녹화 • 대본 • 대여권 • 댄스 • 도형저작물 • 동일성 유지권 • 등록 • 등재 • 디자인 • 디자인권 • 디자인보호법 • 디지털 워터마킹 • 라이선스 • 명품 • 모방 • 모작 • 모조품 • 무용 • 문학 • 미술 • 미술가 • 미술저작물 • 발견 • 발명 • 발명가 • 발명자 • 발명진흥법 • 발명품 • 방송권 • 배우 • 배포 • 배포권 • 번안 • 번역 • 번역기 • 번역물 • 베른협약 • 변경 • 변조 • 변형 • 복제 • 복제권 • 복제물 • 불법복제 • 사본 • 사진저작물 • 산업재산권 • 상표권 • 상표법 • 상호 • 서비스표 • 성명표시권 • 세계지식재산권기구(WIPO) • 소설 • 소유 • 수록 • 시 • 시나리오 • 신기술인증 • 신문 • 신지식재산권 • 실연 • 실연자 • 실용신안 • 실용신안권 • 실용신안법 • 어문저작물 • 연주 • 연주자 • 영상 • 영상저작물 • 영상제작 • 영업표 • 영화 • 영화저작물 • 예술가 • 오디오북 • 오마주 • 워터마크 • 워터마킹 • 원곡 • 원본 • 원작 • 원저작물 • 원저작자(원작자) • 위변조 • 위조 • 위조품 • 음악 • 음악가 • 음악저작물 • 이용허락 • 인쇄 • 인쇄물 • 인쇄소 • 인증 • 자동번역 • 작곡 • 작곡가 • 작사 • 작사가 • 작품 • 잡지 • 장르 • 재산 • 재산권 • 저작권 • 저작권법 • 저작권자 • 저작권 침해 • 저작물 • 저작인격권 • 저작인접권 • 저작인접권자 • 저작자 • 저작재산권 • 저작재산권자 • 전송 • 전송권 • 전시권 • 전자책(이북) • 전자출판물 • 정품 • 조각 • 조각가 • 지분권 • 지식재산권 • 진본 • 진품 • 짝퉁 • 창작 • 창작물 • 창작성 • 창작자 • 책 • 총유 • 출판 • 출판권 • 출판사 • 출판권자 • 출판물 • 출판자 • 춤 • 컴퓨터 프로그램 저작물 • 크리에이티브 커먼즈 라이선스(CCL) • 파리협약 • 패러디 • 퍼블릭 도메인 • 편곡 • 편곡가 • 편집저작물 • 표절 • 합유 • 화가 • 회화 특허 국내특허 • 국제특허(해외특허) • 등재특허 • 디자인특허 • 물질특허 • 발명특허 • 변리사 • 선언특허 • 신약특허 • 용도특허 • 원천특허 • 제조특허 • 제형특허 • 조성물특허 • 출원 • 출원인 • 특허 • 특허괴물 • 특허권 • 특허권자 • 특허기술 • 특허등록 • 특허법 • 특허소송 • 특허증 • 특허청 • 특허출원 • 특허협력조약 • 표준특허 위키 : 자동차, 교통, 지역, 지도, 산업, 기업, 단체, 업무, 생활, 쇼핑, 블록체인, 암호화폐, 인공지능, 개발, 인물, 행사, 일반