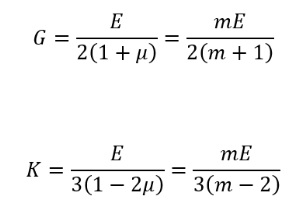"탄성변형"의 두 판 사이의 차이
(→참고자료) |
잔글 (→같이 보기) |
||
| (다른 사용자 한 명의 중간 판 4개는 보이지 않습니다) | |||
| 6번째 줄: | 6번째 줄: | ||
탄성변형은 외력에 의해 물체에 발생된 변형이 탄성한도를 넘지 않는 상태에서의 변형이다. 구조물이 변형되는 정도를 나타내는 변형률은 가해지는 응력에 따라 변하게 된다. 대체로 작은 인장력을 받는 대부분의 금속 재료에서 응력과 변형률은 위 그림과 같은 관계식을 만족하게 되고, 이를 훅의 법칙(Hooke's Law)이라 한다. 비례상수 E는 탄성 계수(Elastic modulus) 혹은 영의 계수(Young's modulus)라 하며 단위는 GPa(기가 파스칼)이다. 즉 탄성계수는 응력-변형률 그래프의 접선 기울기를 의미한다. 따라서 기울기가 가파를수록(E가 클수록) 인장 시편의 재료가 강한 결합을 하고 있음을 추측할 수 있다. 탄성 계수가 클수록 재료의 변형이 잘 일어나지 않으며 주어진 응력에서 변형률을 더욱 작아진다. 시편의 [[온도]]가 증가하면 원자간의 결합력이 약해지고 이에 따라서 원자들의 구속력이 약해져 탄성계수가 낮아짐을 예상해볼 수 있다. | 탄성변형은 외력에 의해 물체에 발생된 변형이 탄성한도를 넘지 않는 상태에서의 변형이다. 구조물이 변형되는 정도를 나타내는 변형률은 가해지는 응력에 따라 변하게 된다. 대체로 작은 인장력을 받는 대부분의 금속 재료에서 응력과 변형률은 위 그림과 같은 관계식을 만족하게 되고, 이를 훅의 법칙(Hooke's Law)이라 한다. 비례상수 E는 탄성 계수(Elastic modulus) 혹은 영의 계수(Young's modulus)라 하며 단위는 GPa(기가 파스칼)이다. 즉 탄성계수는 응력-변형률 그래프의 접선 기울기를 의미한다. 따라서 기울기가 가파를수록(E가 클수록) 인장 시편의 재료가 강한 결합을 하고 있음을 추측할 수 있다. 탄성 계수가 클수록 재료의 변형이 잘 일어나지 않으며 주어진 응력에서 변형률을 더욱 작아진다. 시편의 [[온도]]가 증가하면 원자간의 결합력이 약해지고 이에 따라서 원자들의 구속력이 약해져 탄성계수가 낮아짐을 예상해볼 수 있다. | ||
| − | 탄성변형은 [[고체]]내 [[원자]]들 간의 [[화학]]적 결합을 끊는 것이 아닌 당기는 변형으로 원자간의 거리 변화가 재료 전체에 걸쳐 누적되어서 거시적으로 나타난 형태로 힘을 제거하게 되면 원상태로 돌아오게 된다. 응력과 변형이 선형적인 관계를 가진다. 원자간의 거리가 멀어지게 되면 인력이 발생하고 가까워지면 척력이 발생한다.<ref>모설, 〈[https://new-material.tistory.com/126 변형- 탄성 변형/ 소성 변형/ 크리프 변형]〉, 《티스토리》, 2020- | + | 탄성변형은 [[고체]]내 [[원자]]들 간의 [[화학]]적 결합을 끊는 것이 아닌 당기는 변형으로 원자간의 거리 변화가 재료 전체에 걸쳐 누적되어서 거시적으로 나타난 형태로 힘을 제거하게 되면 원상태로 돌아오게 된다. 응력과 변형이 선형적인 관계를 가진다. 원자간의 거리가 멀어지게 되면 인력이 발생하고 가까워지면 척력이 발생한다.<ref>모설, 〈[https://new-material.tistory.com/126 변형- 탄성 변형/ 소성 변형/ 크리프 변형]〉, 《티스토리》, 2020-04-29</ref><ref>〈[https://terms.naver.com/entry.naver?docId=1620797&cid=50313&categoryId=50313 탄성 변형(elastic deformation)]〉, 《네이버 지식백과》</ref> |
==훅의 법칙(Hooke's Law)== | ==훅의 법칙(Hooke's Law)== | ||
| 17번째 줄: | 17번째 줄: | ||
==푸아송비(Possion`s ratio)== | ==푸아송비(Possion`s ratio)== | ||
| − | 재료 내부에 생기는 응력에 의한 가로 변형률과 세로변형률의 비로써 동일 재료에서는 탄성한도 내에서 일정한 비를 나타내며 재료상수 중 하나이다.<ref>일상탈출, 〈[https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=jhwoo1124&logNo=221496805217 탄성변형(수직응력)]〉, 《네이버 블로그》, 2019- | + | 재료 내부에 생기는 응력에 의한 가로 변형률과 세로변형률의 비로써 동일 재료에서는 탄성한도 내에서 일정한 비를 나타내며 재료상수 중 하나이다.<ref>일상탈출, 〈[https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=jhwoo1124&logNo=221496805217 탄성변형(수직응력)]〉, 《네이버 블로그》, 2019-03-25</ref> |
[[파일:푸아송비.jpg|썸네일|580픽셀|가운데|]] | [[파일:푸아송비.jpg|썸네일|580픽셀|가운데|]] | ||
| 52번째 줄: | 52번째 줄: | ||
* 〈[https://terms.naver.com/entry.naver?docId=1620797&cid=50313&categoryId=50313 탄성 변형]〉, 《네이버 지식백과》 | * 〈[https://terms.naver.com/entry.naver?docId=1620797&cid=50313&categoryId=50313 탄성 변형]〉, 《네이버 지식백과》 | ||
* 〈[https://terms.naver.com/entry.naver?docId=1620797&cid=50313&categoryId=50313 탄성 변형(elastic deformation)]〉, 《네이버 지식백과》 | * 〈[https://terms.naver.com/entry.naver?docId=1620797&cid=50313&categoryId=50313 탄성 변형(elastic deformation)]〉, 《네이버 지식백과》 | ||
| − | * 모설, 〈[https://new-material.tistory.com/126 변형- 탄성 변형/ 소성 변형/ 크리프 변형]〉, 《티스토리》, 2020- | + | * 모설, 〈[https://new-material.tistory.com/126 변형- 탄성 변형/ 소성 변형/ 크리프 변형]〉, 《티스토리》, 2020-04-29 |
| − | * 일상탈출, 〈[https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=jhwoo1124&logNo=221496805217 탄성변형(수직응력)]〉, 《네이버 블로그》, 2019- | + | * 일상탈출, 〈[https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=jhwoo1124&logNo=221496805217 탄성변형(수직응력)]〉, 《네이버 블로그》, 2019-03-25 |
* the artlsan, 〈[https://factoryforvalue.tistory.com/238 변형율과 탄성계수]〉, 《티스토리》, 2021-08-10 | * the artlsan, 〈[https://factoryforvalue.tistory.com/238 변형율과 탄성계수]〉, 《티스토리》, 2021-08-10 | ||
== 같이 보기 == | == 같이 보기 == | ||
| − | * [[ | + | * [[탄성]] |
| + | * [[변형]] | ||
| + | * [[소성변형]] | ||
| + | * [[고체]] | ||
| + | * [[원자]] | ||
| + | * [[화학]] | ||
| + | * [[온도]] | ||
| + | * [[탄소]] | ||
| + | * [[철근]] | ||
{{자동차 제조|검토 필요}} | {{자동차 제조|검토 필요}} | ||
2022년 7월 23일 (토) 11:22 기준 최신판
탄성변형(elastic deformation, 彈性變形)은 외력에 의해서 발생한 변형이 외력을 제거하여 완전히 회복하는 변형이다. 이에 대해 변형이 전혀 회복되지 않는 경우를 소성변형이라 한다.[1]
목차
개요[편집]
탄성변형은 외력에 의해 물체에 발생된 변형이 탄성한도를 넘지 않는 상태에서의 변형이다. 구조물이 변형되는 정도를 나타내는 변형률은 가해지는 응력에 따라 변하게 된다. 대체로 작은 인장력을 받는 대부분의 금속 재료에서 응력과 변형률은 위 그림과 같은 관계식을 만족하게 되고, 이를 훅의 법칙(Hooke's Law)이라 한다. 비례상수 E는 탄성 계수(Elastic modulus) 혹은 영의 계수(Young's modulus)라 하며 단위는 GPa(기가 파스칼)이다. 즉 탄성계수는 응력-변형률 그래프의 접선 기울기를 의미한다. 따라서 기울기가 가파를수록(E가 클수록) 인장 시편의 재료가 강한 결합을 하고 있음을 추측할 수 있다. 탄성 계수가 클수록 재료의 변형이 잘 일어나지 않으며 주어진 응력에서 변형률을 더욱 작아진다. 시편의 온도가 증가하면 원자간의 결합력이 약해지고 이에 따라서 원자들의 구속력이 약해져 탄성계수가 낮아짐을 예상해볼 수 있다.
탄성변형은 고체내 원자들 간의 화학적 결합을 끊는 것이 아닌 당기는 변형으로 원자간의 거리 변화가 재료 전체에 걸쳐 누적되어서 거시적으로 나타난 형태로 힘을 제거하게 되면 원상태로 돌아오게 된다. 응력과 변형이 선형적인 관계를 가진다. 원자간의 거리가 멀어지게 되면 인력이 발생하고 가까워지면 척력이 발생한다.[2][3]
훅의 법칙(Hooke's Law)[편집]
비례한도 내에서 응력은 변형률에 비례한다.
E : 탄성계수(elastic modulus), 세로(종) 탄성계수(longitudinal elastic modulus), 영률(Young's modulus)
- 응력 변형률 선도에서 O-A의 기울기 즉, 변형률(무차원수)로 나눈 응력의 단위를 가지므로 탄성계수는 응력과 동일한 단위를 가진다.
푸아송비(Possion`s ratio)[편집]
재료 내부에 생기는 응력에 의한 가로 변형률과 세로변형률의 비로써 동일 재료에서는 탄성한도 내에서 일정한 비를 나타내며 재료상수 중 하나이다.[4]
탄성 계수[편집]
탄성 계수(Modulus of elasticity, 憚性係數)는 고체 역학에서 재료의 강성도(stiffness)를 나타내는 값이다. 탄성 계수는 응력과 변형도의 비율로 정의된다. 재료의 시험편에 대한 인장 또는 전단 시험으로 얻은 응력-변형도 선도의 탄성 구간 기울기로부터 탄성 계수를 결정할 수 있다. 인장 탄성 계수는 “영률”(Young's modulus)이라고도 불리는데, 이는 영국의 학자인 토마스 영(Thomas Young)의 이름을 따서 붙여진 것이다.
탄성 계수는 하중에 대한 재료의 반응을 계산할 수 있게 한다. 예를 들어, 인장이 작용하는 강선이 얼마나 늘어날 것인지, 또는 압축을 받는 기둥이 어떤 하중 아래에서 좌굴될 것인지를 예측할 수 있다.
선형과 비선형[편집]
많은 재료는 일정 구간의 변형도에 대해 상수의 탄성 계수를 갖는다. 이런 종류의 재료를 선형 재료라고 하며, 훅의 법칙을 따른다고 한다. 이런 재료에는 강, 탄소 섬유와 유리 등이 있다. 고무나 (아주 작은 변형도를 벗어나는) 흙은 비선형 재료이다.
비등방성 재료[편집]
비등방성 재료는 하중이 작용하는 방향에 따라 탄성 계수의 값이 다르다. 이런 비등방성 재료에는 탄소 섬유, 목재와 철근 콘크리트 등이 있다.[5]
계산[편집]
세로탄성계수(youngs modulus, 영률, E)[편집]
재료가 탄성한도 내에서 하중을 받을때 일정한 비례를 가지는데 이때의 관계비
가로탄성계수(shearing modulus, 전단탄성계수)[편집]
전단응력에 대한 재료의 탄성계수
강성율
G=τ/γ
체적탄성계수(bulk modulus, 부피탄성계수, K)[편집]
재료에 하중이 가해졌을대 하중에 대한 부피방향으로의 탄성계수[6]
K=p/εv
탄성계수간 관계[편집]
각주[편집]
- ↑ 〈탄성 변형〉, 《네이버 지식백과》
- ↑ 모설, 〈변형- 탄성 변형/ 소성 변형/ 크리프 변형〉, 《티스토리》, 2020-04-29
- ↑ 〈탄성 변형(elastic deformation)〉, 《네이버 지식백과》
- ↑ 일상탈출, 〈탄성변형(수직응력)〉, 《네이버 블로그》, 2019-03-25
- ↑ 〈탄성 계수〉, 《위키백과》
- ↑ the artlsan, 〈변형율과 탄성계수〉, 《티스토리》, 2021-08-10
참고자료[편집]
- 〈탄성 계수〉, 《위키백과》
- 〈탄성 변형〉, 《네이버 지식백과》
- 〈탄성 변형(elastic deformation)〉, 《네이버 지식백과》
- 모설, 〈변형- 탄성 변형/ 소성 변형/ 크리프 변형〉, 《티스토리》, 2020-04-29
- 일상탈출, 〈탄성변형(수직응력)〉, 《네이버 블로그》, 2019-03-25
- the artlsan, 〈변형율과 탄성계수〉, 《티스토리》, 2021-08-10
같이 보기[편집]

 위키원
위키원